Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the Euler–Lagrange differential equations derived from a given functional
ResourceFunction["EulerEquations"][f,u[x],x] returns the Euler–Lagrange differential equation obeyed by u[x] derived from the functional f, where f depends on the function u[x] and its derivatives, as well as the independent variable x. | |
ResourceFunction["EulerEquations"][f,u[x,y,…],{x,y,…}] returns the Euler–Lagrange differential equation obeyed by u[x,y,…]. | |
ResourceFunction["EulerEquations"][f,{u[x,y,…],v[x,y,…],…},{x,y,…}] returns a list of Euler–Lagrange differential equations obeyed by u[x,y,…],v[x,y,…],…. |
The Euler equations for the arc length ![]() in two dimensions yields a straight line:
in two dimensions yields a straight line:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= |
A simple pendulum has the Lagrangian ![]() :
:
| In[3]:= |
| Out[3]= |
The solution to the pendulum equation can be expressed using the function JacobiAmplitude:
| In[4]:= |
| Out[4]= | 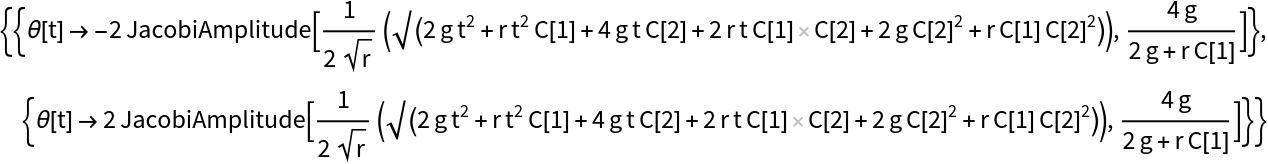 |
The Lagrangian of a point particle in two dimensions has two dependent variables and yields Newton's equations:
| In[5]:= |
| Out[5]= |
The Lagrangian of a point particle in two dimensions with a central potential:
| In[6]:= |
| Out[6]= |
Second- and higher-order derivatives may be included in the integrand. A Lagrangian for motion on a spring using higher-order terms:
| In[7]:= |
| Out[7]= |
The integrand ![]() has several independent variables:
has several independent variables:
| In[8]:= |
| Out[8]= |
The Euler equations yield Laplace's equation:
| In[9]:= |
| Out[9]= |
The Euler equations for the integrand f[yxx,yx,y,x]:
| In[10]:= |
| Out[10]= | 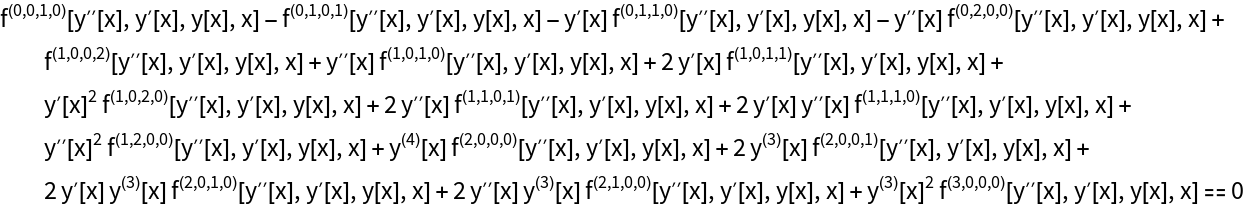 |
The "textbook" answer:
| In[11]:= | ![eqns2 = D[Derivative[1, 0, 0, 0][f][y''[x], y'[x], y[x], x], x, x] - D[Derivative[0, 1, 0, 0][f][y''[x], y'[x], y[x], x], x] + Derivative[0, 0, 1, 0][f][y''[x], y'[x], y[x], x] == 0](https://www.wolframcloud.com/obj/resourcesystem/images/28b/28b9ecbe-4848-4669-a072-99f2958da111/3e24e0eb76d84b6a.png) |
| Out[11]= | 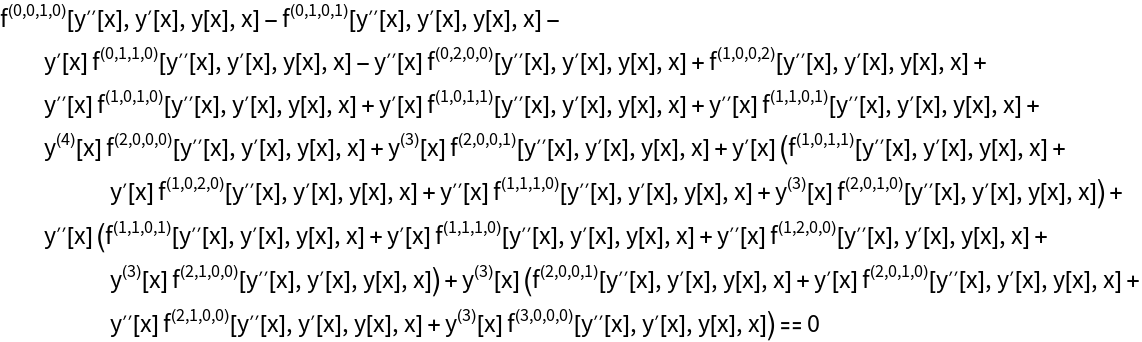 |
Check:
| In[12]:= |
| Out[12]= |
The brachistochrone problem asks for the curve of quickest descent. The time taken for a particle to fall an arc length ds is ![]() . If y measures the decrease in height from an initial point of release, then the velocity v satisfies:
. If y measures the decrease in height from an initial point of release, then the velocity v satisfies:
| In[13]:= |
| Out[13]= |
The equation for a curve joining two points, where a particle starting at rest from the higher point takes the least amount of time to reach the lower point:
| In[14]:= | ![ResourceFunction["EulerEquations"][Sqrt[(
x'[\[Theta]]^2 + y'[\[Theta]]^2)/(
2 g y[\[Theta]])], {x[\[Theta]], y[\[Theta]]}, \[Theta]]](https://www.wolframcloud.com/obj/resourcesystem/images/28b/28b9ecbe-4848-4669-a072-99f2958da111/73c23849e5acdd6d.png) |
| Out[14]= | 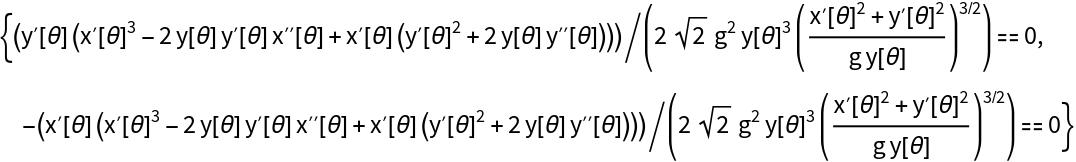 |
It is well known that the solution to the brachistochrone problem is a cycloid:
| In[15]:= | ![% /. {
x -> (k (# - Sin[#]) &),
y -> (k (1 - Cos[#]) &)
} // Simplify](https://www.wolframcloud.com/obj/resourcesystem/images/28b/28b9ecbe-4848-4669-a072-99f2958da111/620238b92a57a629.png) |
| Out[15]= |
The Lagrangian for a vibrating string yields the classical wave equation:
| In[16]:= |
| Out[16]= |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License