Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the multidimensional corner angle
ResourceFunction["ErikssonCornerAngle"][o,{p1,…,pd}] gives the corner angle at the point o and spanned by the vectors p1,…,pd. |
The corner angle at the origin for vectors in two dimensions:
| In[1]:= |
| Out[1]= |
The corner angle at the origin for vectors in three dimensions:
| In[2]:= |
| Out[2]= |
ErikssonCornerAngle works in any number of dimensions:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= | 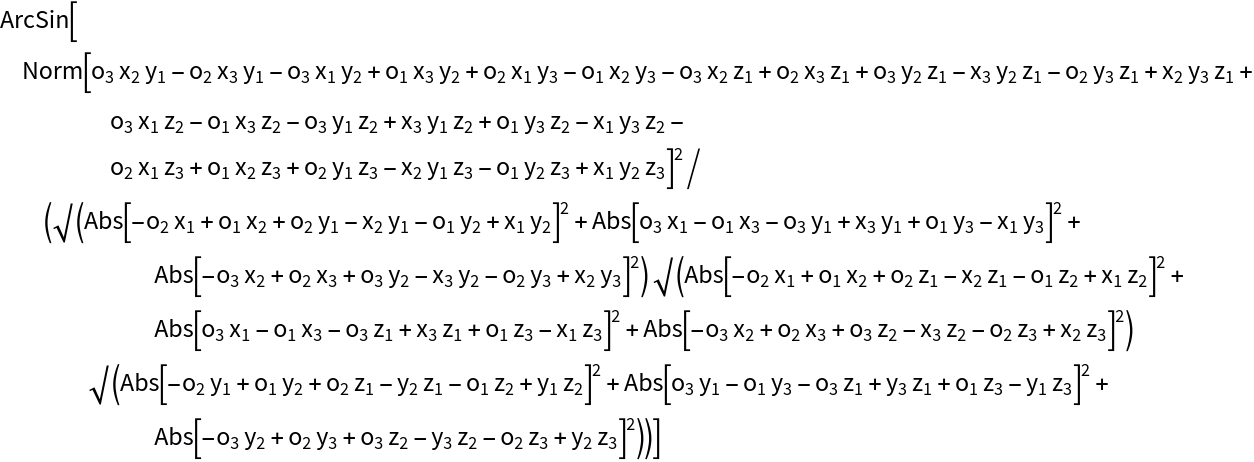 |
| In[5]:= |
| Out[5]= | 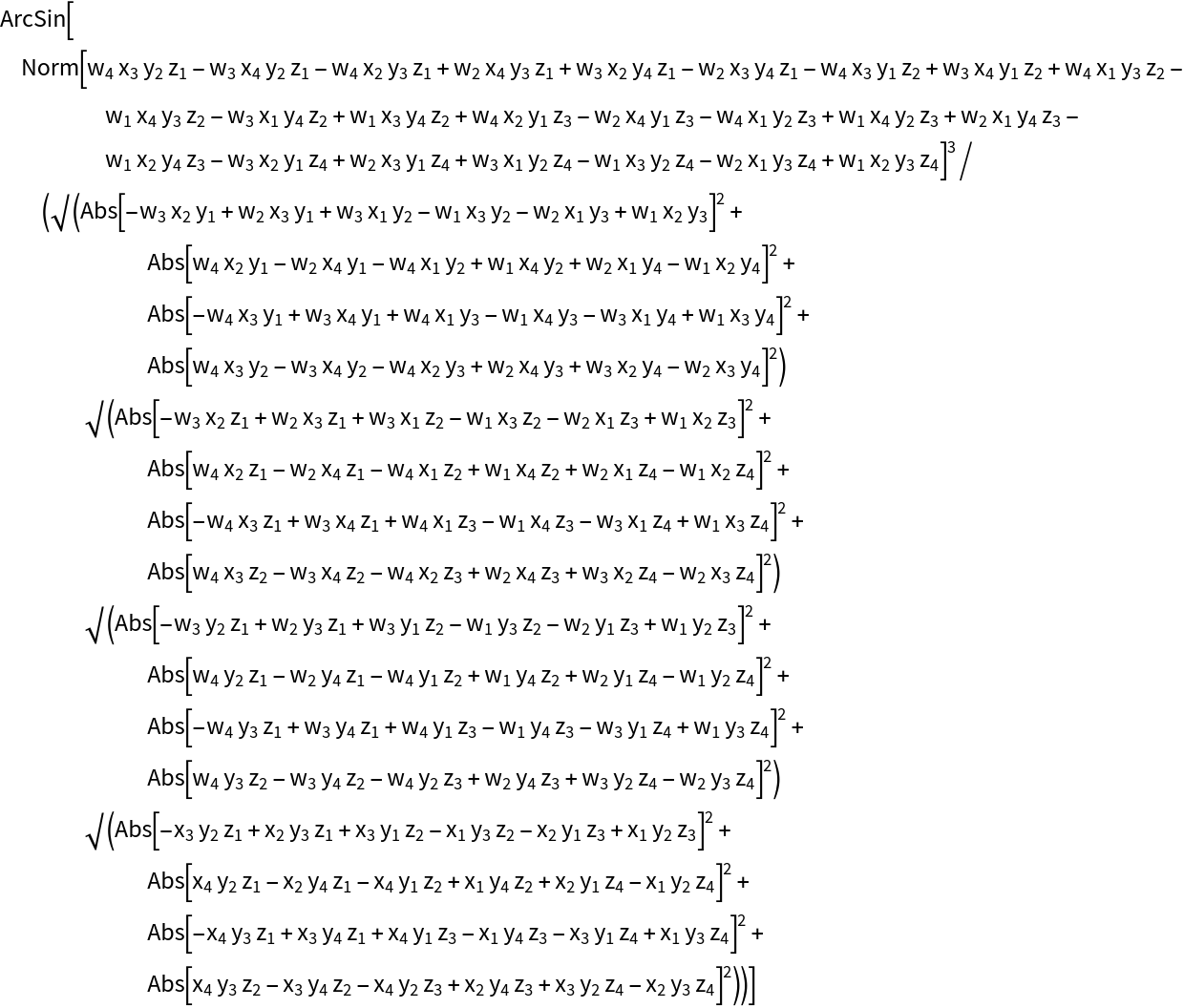 |
Compute the corner angle for various Platonic solids:
| In[6]:= | ![Table[ResourceFunction["ErikssonCornerAngle"][First[#], Rest[#]] &[
PolyhedronData[pla, "VertexCoordinates"][[
Prepend[Cases[PolyhedronData[pla, "EdgeIndices"], {1, k_} :> k], 1]]]], {pla, {"Tetrahedron", "Cube", "Dodecahedron"}}] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/564/56441893-3c14-49c9-880f-c26cafe1ee0d/7729573c16cb3e2a.png) |
| Out[6]= |
Generate a random simplex:
| In[7]:= |
| Out[7]= |  |
Compute all the corner angles of the simplex:
| In[8]:= |
| Out[8]= |
In two dimensions, ErikssonCornerAngle is similar to the results of SolidAngle and PlanarAngle:
| In[9]:= |
| Out[9]= | 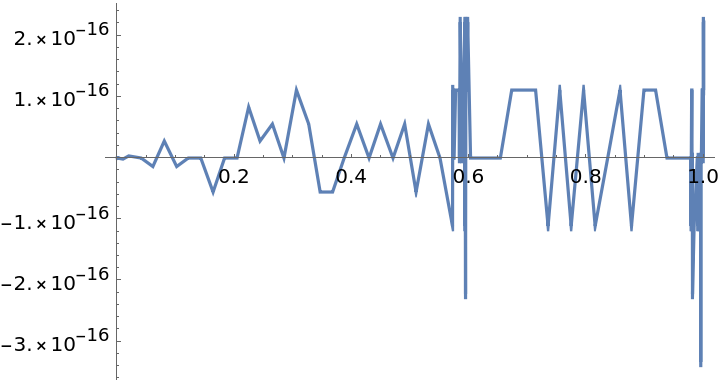 |
In three dimensions, the difference between ErikssonCornerAngle and SolidAngle is more apparent:
| In[10]:= | ![Plot[{SolidAngle[{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}, {1, 1, x}}], ResourceFunction[
"ErikssonCornerAngle"][{0, 0, 0}, {{1, 0, 0}, {0, 1, 0}, {1, 1, x}}]}, {x, 0, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/564/56441893-3c14-49c9-880f-c26cafe1ee0d/4de446ee95d7d1da.png) |
| Out[10]= | 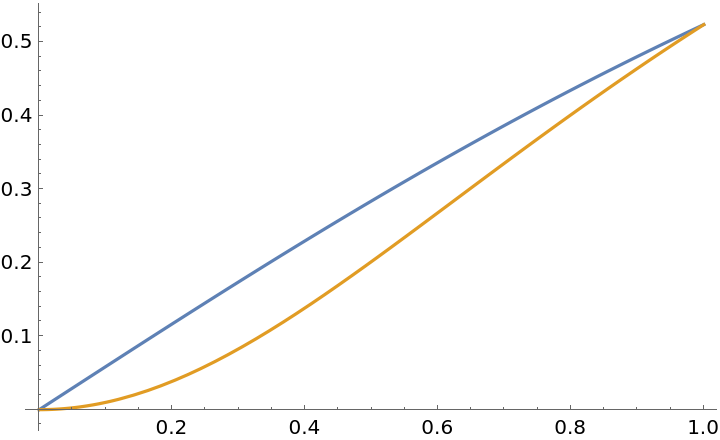 |
This work is licensed under a Creative Commons Attribution 4.0 International License