Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Erfci

Source Notebook

Evaluate the integral of the complementary error function

Contributed by: Paco Jain (Wolfram Research)

ResourceFunction["Erfci"][x]

computes the definite integral of erfc(x).

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
The ResourceFunction["Erfci"] function is defined by the integral -Integrate[Erfc[t],{t,x,∞}]. In closed form, this is equivalent to -Exp[-x^2]/Sqrt[π] + x Erfc[x].
ResourceFunction["Erfci"] can be evaluated to arbitrary numerical precision.
ResourceFunction["Erfci"] automatically threads over lists.

Examples

Basic Examples (2) 

Plot the Erfci function:

In[1]:=
Plot[ResourceFunction["Erfci"][x], {x, -2, 2}]
Out[1]=

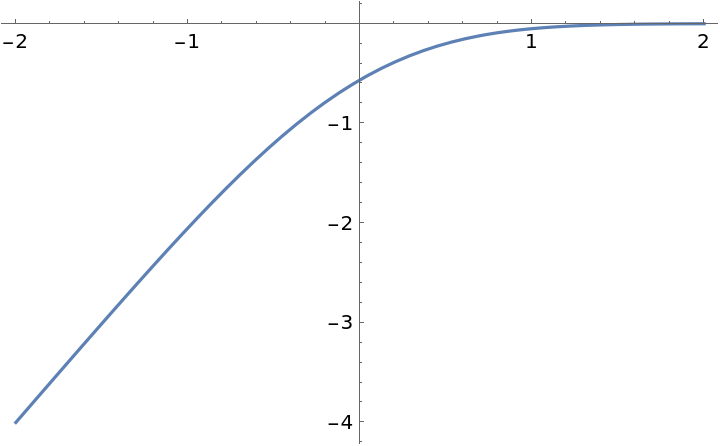
Examine some particular values:

In[2]:=
ResourceFunction["Erfci"][0]
Out[2]=
In[3]:=
ResourceFunction["Erfci"][2]
Out[3]=

Scope (3) 

Erfci can be applied to complex values:

In[4]:=
ResourceFunction["Erfci"][2 + 3 I]
Out[4]=
In[5]:=
% // N
Out[5]=

When applied to numerical values, Erfci reflects the precision of its input:

In[6]:=
ResourceFunction["Erfci"][N[Pi, 100]]
Out[6]=

Erfci threads elementwise over lists:

In[7]:=
ResourceFunction["Erfci"][{1.2, 2.3, 4.7}]
Out[7]=

Applications (1) 

Plot Erfci over a subset of the complexes:

In[8]:=
ComplexPlot3D[ResourceFunction["Erfci"][z], {z, 3}, PlotLegends -> Automatic]
Out[8]=

Requirements

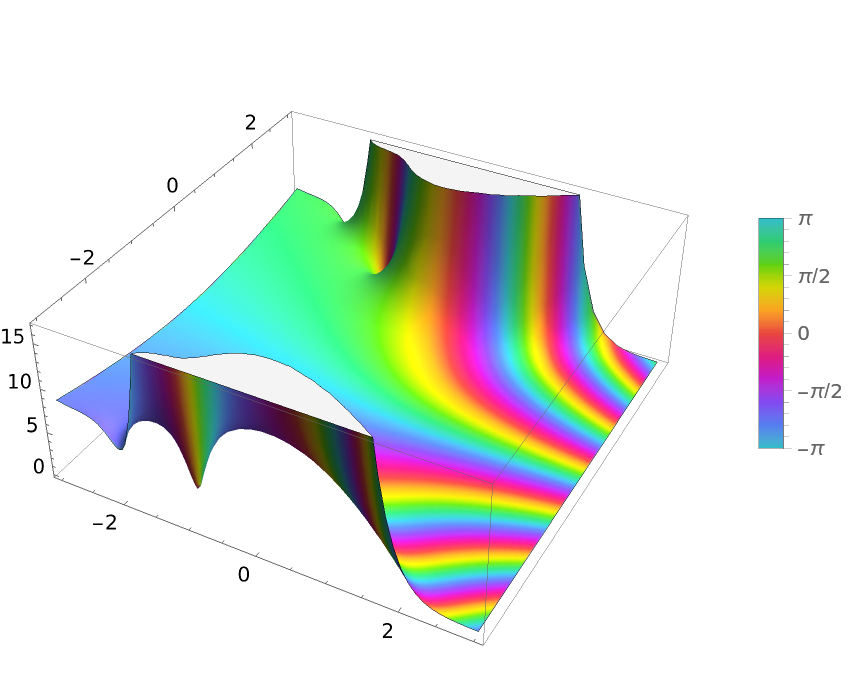
Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 14 September 2021
  • 1.0.0 – 27 February 2019

Related Resources

License Information