Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Epstein–Hubbell integral
ResourceFunction["EpsteinHubbellOmega"][n,m] gives the Epstein–Hubbell integral Ωn(m). |
Evaluate numerically:
| In[1]:= |
| Out[1]= |
Plot Ω2(m):
| In[2]:= |
| Out[2]= | 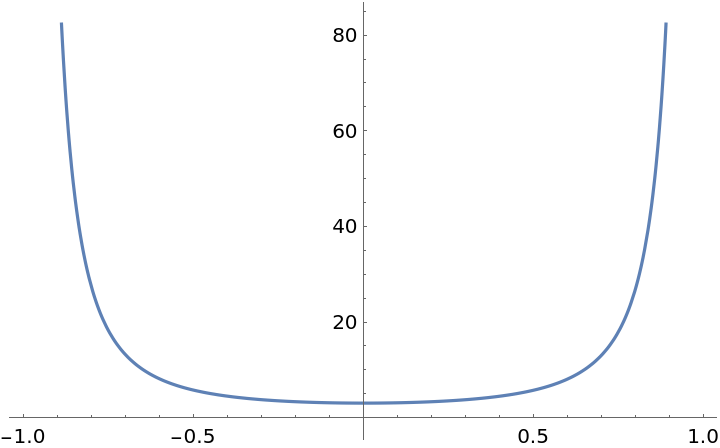 |
Series at the origin:
| In[3]:= |
| Out[3]= |
Evaluate for complex arguments and orders:
| In[4]:= |
| Out[4]= |
Evaluate to high precision:
| In[5]:= |
| Out[5]= |
The precision of the output tracks the precision of the input:
| In[6]:= |
| Out[6]= |
EpsteinHubbellOmega threads elementwise over lists:
| In[7]:= |
| Out[7]= |
Log plot of a family of Epstein–Hubbell integrals:
| In[8]:= | ![LogPlot[Table[
ResourceFunction["EpsteinHubbellOmega"][j, m], {j, 0, 9}] // Evaluate, {m, 0, 1}, AspectRatio -> GoldenRatio, PlotRange -> {0, 10^4}]](https://www.wolframcloud.com/obj/resourcesystem/images/78a/78ab4a81-5774-447b-ab30-4d238c045232/2e3c3deebb3d9ed8.png) |
| Out[8]= | 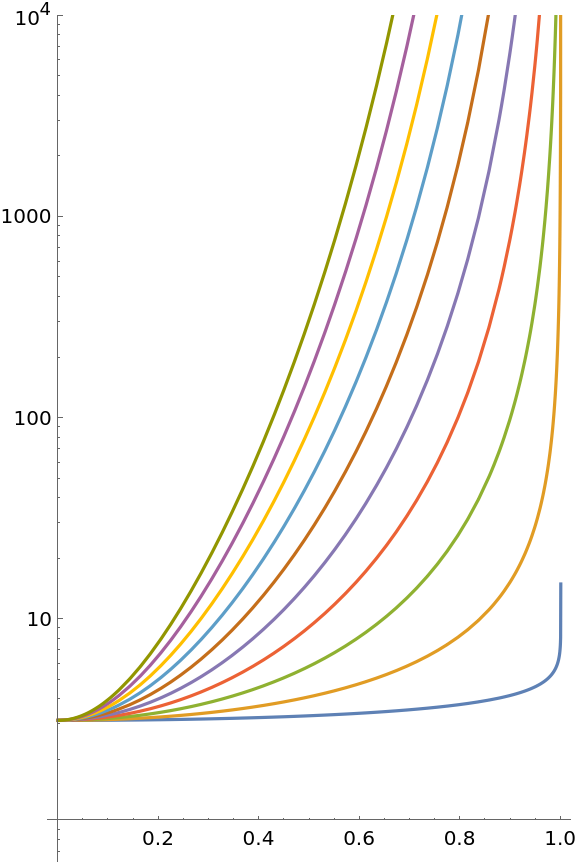 |
For integer n, EpsteinHubbellOmega can be expressed in terms of EllipticE and EllipticK:
| In[9]:= |
| Out[9]= | 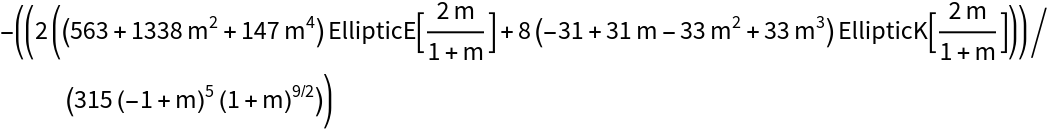 |
For integer n, EpsteinHubbellOmega can be expressed in terms of half-integer order LegendreP:
| In[10]:= | ![With[{n = 6, m = N[2/3, 20]},
{\[Pi]/(1 - m^2)^((2 n + 1)/4) LegendreP[n - 1/2, 1/Sqrt[1 - m^2]], ResourceFunction["EpsteinHubbellOmega"][n, m]}]](https://www.wolframcloud.com/obj/resourcesystem/images/78a/78ab4a81-5774-447b-ab30-4d238c045232/4e246f1615eb2f0c.png) |
| Out[10]= |
For integer n, EpsteinHubbellOmega can be expressed in terms of LegendreQ:
| In[11]:= | ![With[{n = 6, m = N[2/3, 20]},
{((-1)^n 2^(2 n + 1/2) n!)/((2 n)! Sqrt[m] (1 - m^2)^(n/2))
LegendreQ[-1/2, n, 3, 1/m], ResourceFunction["EpsteinHubbellOmega"][n, m]}]](https://www.wolframcloud.com/obj/resourcesystem/images/78a/78ab4a81-5774-447b-ab30-4d238c045232/0bf021b78da1e46a.png) |
| Out[11]= |
Express an Epstein–Hubbell integral of noninteger order in terms of simpler functions:
| In[12]:= |
| Out[12]= | 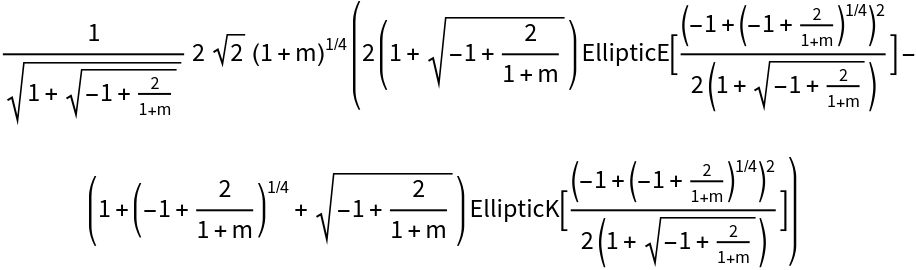 |
Compare EpsteinHubbellOmega with the integral definition:
| In[13]:= | ![With[{n = 5, m = 2/3, prec = 20},
{N[ResourceFunction["EpsteinHubbellOmega"][n, m], prec],
NIntegrate[(1 - m Cos[t])^(-n - 1/2), {t, 0, Pi}, WorkingPrecision -> prec]}]](https://www.wolframcloud.com/obj/resourcesystem/images/78a/78ab4a81-5774-447b-ab30-4d238c045232/44bf3fd5d5796be3.png) |
| Out[13]= |
This work is licensed under a Creative Commons Attribution 4.0 International License