Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EllipticRationalR

Source Notebook

Evaluate the elliptic rational function

Contributed by: Jan Mangaldan

ResourceFunction["EllipticRationalR"][n,ξ,x]

gives the elliptic rational function Rn(ξ,x).

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
The elliptic rational function with degree n and selectivity factor ξ is defined as , where cd(u❘m) is the Jacobi elliptic function JacobiCD, cd-1(v❘m) is InverseJacobiCD, K(m) is the complete elliptic integral of the first kind EllipticK and ℒn(ξ)=Rn(ξ,ξ) is the largest value of Rn(ξ,x) for Abs[x]>1, and is referred to as the discrimination factor.
ResourceFunction["EllipticRationalR"] can be evaluated to arbitrary numerical precision.
ResourceFunction["EllipticRationalR"] automatically threads over lists.

Examples

Basic Examples (2) 

Evaluate numerically:

In[1]:=
ResourceFunction["EllipticRationalR"][2, 1.2, 0.8]
Out[1]=

Plot R5(1.1,x):

In[2]:=
Plot[ResourceFunction["EllipticRationalR"][5, 1.1, x], {x, -1, 1}]
Out[2]=

Scope (3) 

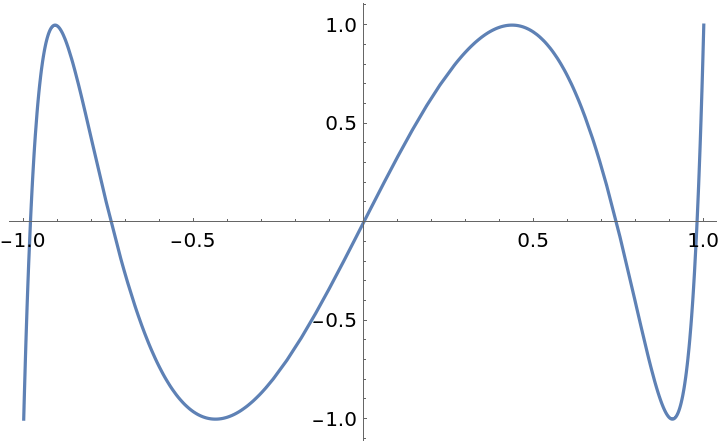Evaluate symbolically:

In[3]:=
ResourceFunction["EllipticRationalR"][4, 3/2, x]
Out[3]=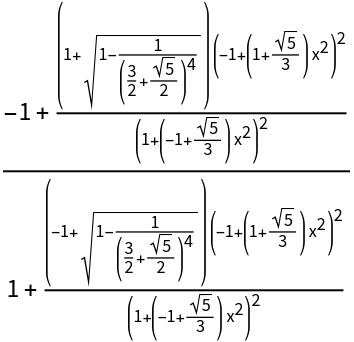

Evaluate to high precision:

In[4]:=
N[ResourceFunction["EllipticRationalR"][12, 11/10, 3/4], 50]
Out[4]=

The precision of the output tracks the precision of the input:

In[5]:=
ResourceFunction["EllipticRationalR"][12, 11/10, 0.7500000000000000000000000000000000]
Out[5]=

EllipticRationalR threads elementwise over lists:

In[6]:=
ResourceFunction["EllipticRationalR"][12, 11/10, {0.2, 0.4, 0.6}]
Out[6]=

Applications (2) 

Compare an elliptic rational function and a Chebyshev polynomial:

In[7]:=
Manipulate[ Plot[{ResourceFunction["EllipticRationalR"][n, \[Xi], x], ChebyshevT[n, x]}, {x, -1, 1}, Axes -> None, Frame -> True, PlotRange -> All], {{n, 5}, 1, 10, 1}, {{\[Xi], 1.1}, 1.001, 5}, SaveDefinitions -> True]
Out[7]=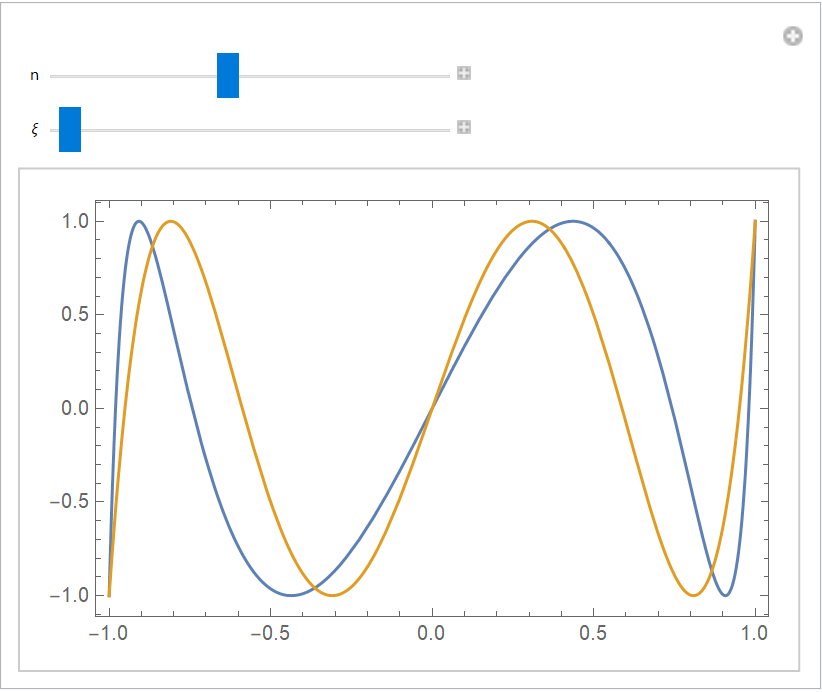

Use the elliptic rational function to construct the best minimax approximation of a unit square pulse:

In[8]:=
With[{\[CurlyEpsilon] = 0.01, n = 32, \[Xi] = 1.0001}, Plot[1/(1 + \[CurlyEpsilon]^2 ResourceFunction["EllipticRationalR"][ n, \[Xi], x]^2), {x, 0, 2}, Exclusions -> None]]
Out[8]=

Compare with an approximation using ChebyshevT:

In[9]:=
With[{\[CurlyEpsilon] = 0.01, n = 32, \[Xi] = 1.0001}, Plot[{1/(1 + \[CurlyEpsilon]^2 ResourceFunction["EllipticRationalR"][ n, \[Xi], x]^2), 1/( 1 + \[CurlyEpsilon]^2 ChebyshevT[n, x]^2)}, {x, 0.95, 1.05}, AxesOrigin -> {0.95, 0}]]
Out[9]=

Properties and Relations (2) 

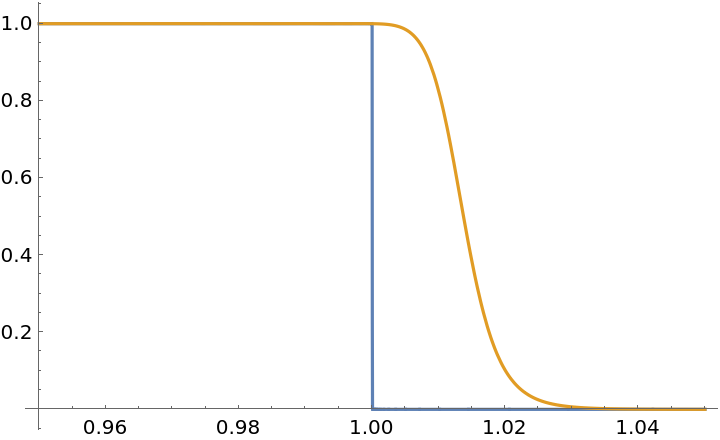Compare EllipticRationalR with the definition:

In[10]:=
With[{n = 6, \[Xi] = 4/3}, {ResourceFunction["EllipticRationalR"][6, \[Xi], x], JacobiCD[ n EllipticK[ ResourceFunction["EllipticRationalR"][n, \[Xi], \[Xi]]^-2]/ EllipticK[\[Xi]^-2] InverseJacobiCD[x, 1/\[Xi]^2], 1/ ResourceFunction["EllipticRationalR"][n, \[Xi], \[Xi]]^2]} /. x -> RandomReal[{-1, 1}]]
Out[10]=

Verify the inversion identity:

In[11]:=
With[{n = 6, \[Xi] = 4/3}, FullSimplify[ ResourceFunction["EllipticRationalR"][n, \[Xi], x] == ResourceFunction["EllipticRationalR"][n, \[Xi], \[Xi]]/ ResourceFunction["EllipticRationalR"][n, \[Xi], \[Xi]/x], x \[Element] Reals]]
Out[11]=

Version History

  • 1.0.0 – 24 March 2021

Source Metadata

  • Citation:
    • Lutovac M.D., Tosic D.V., Evans B.L., Filter Design for Signal Processing Using MATLAB and Mathematica. Upper Saddle River, NJ: Prentice Hall, 2001.
    • Lutovac M.D., Tosic D.V., "Elliptic Rational Functions." The Mathematica Journal, vol. 9, no. 3, 2004.

Related Resources

License Information