Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EllipticExpand

Source Notebook

Expand elliptic functions in an expression

Contributed by: Jan Mangaldan

ResourceFunction["EllipticExpand"][expr]

expands out elliptic functions in expr.

Details and Options

ResourceFunction["EllipticExpand"] operates on both Jacobi and Weierstrass elliptic functions.
ResourceFunction["EllipticExpand"] splits up sums and integer multiples that appear in arguments of elliptic functions, using elliptic function identities when possible.
For expressions containing Jacobi elliptic functions, ResourceFunction["EllipticExpand"] produces an equivalent expression entirely in terms of JacobiSN, JacobiCN and JacobiDN.
ResourceFunction["EllipticExpand"] accepts the following options:
"ExpandJacobi"Truewhether to expand Jacobi functions
"ExpandNonElliptic"Falsewhether to expand non-elliptic functions
"ExpandWeierstrass"Truewhether to expand Weierstrass functions
With "ExpandNonElliptic"→True, ResourceFunction["EllipticExpand"] expands out all instances of JacobiEpsilon (if "ExpandJacobi"→True) and WeierstrassZeta (if "ExpandWeierstrass"→True).
ResourceFunction["EllipticExpand"] automatically threads over lists, as well as equations, inequalities and logic functions.

Examples

Basic Examples (2) 

Expand Jacobi elliptic function expressions:

In[1]:=
ResourceFunction["EllipticExpand"][JacobiSN[2 z, m]]
Out[1]=
In[2]:=
ResourceFunction["EllipticExpand"][JacobiSN[u + v, m]]
Out[2]=

Expand Weierstrass elliptic function expressions:

In[3]:=
ResourceFunction["EllipticExpand"][ WeierstrassP[2 z, {Subscript[g, 2], Subscript[g, 3]}]]
Out[3]=
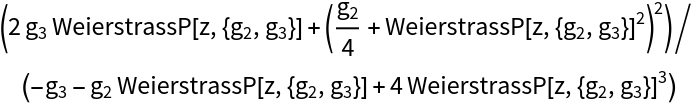
In[4]:=
ResourceFunction["EllipticExpand"][ WeierstrassP[u + v, {Subscript[g, 2], Subscript[g, 3]}]]
Out[4]=

Scope (4) 

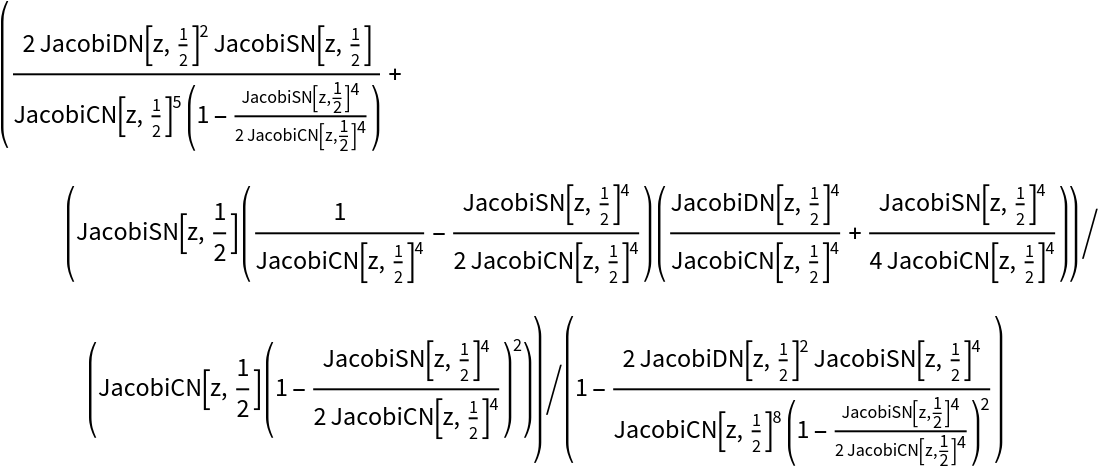
Expand Jacobi elliptic function expressions:

In[5]:=
ResourceFunction["EllipticExpand"][JacobiSC[3 z, 1/2]]
Out[5]=
In[6]:=
ResourceFunction["EllipticExpand"][JacobiND[x + y + z, 2/3]]
Out[6]=

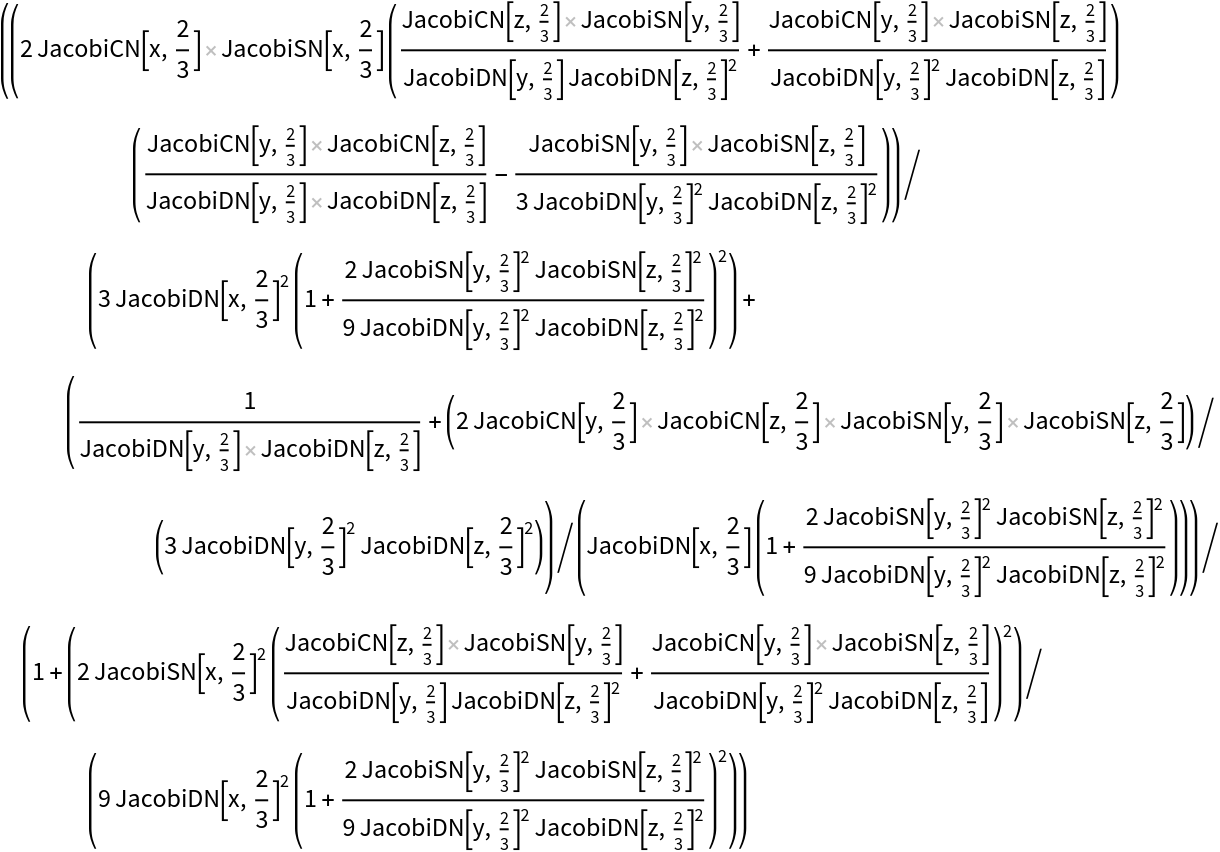
Expand Weierstrass elliptic function expressions:

In[7]:=
ResourceFunction["EllipticExpand"][WeierstrassPPrime[3 z, {4, 0}]]
Out[7]=
In[8]:=
ResourceFunction["EllipticExpand"][WeierstrassP[x + y + z, {0, 4}]]
Out[8]=

EllipticExpand threads over lists:

In[9]:=
ResourceFunction[ "EllipticExpand"][{JacobiDC[x - I y, 1/2], WeierstrassPPrime[2 t, {0, 1}]}]
Out[9]=

EllipticExpand threads over equations and inequalities:

In[10]:=
ResourceFunction["EllipticExpand"][1 < JacobiSD[2 t/5, 1/3] < 2]
Out[10]=

Options (6) 

ExpandJacobi (2) 

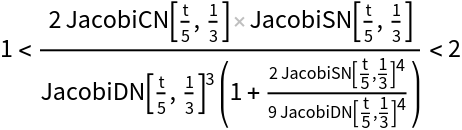
With the setting "ExpandJacobi"→True, Jacobi elliptic functions are expanded out:

In[11]:=
ResourceFunction[ "EllipticExpand"][{JacobiDC[u - v, m], WeierstrassP[u - v, {g2, g3}]}, "ExpandJacobi" -> True]
Out[11]=

With the setting "ExpandJacobi"→False, Jacobi elliptic functions are left untouched:

In[12]:=
ResourceFunction[ "EllipticExpand"][{JacobiDC[u - v, m], WeierstrassP[u - v, {g2, g3}]}, "ExpandJacobi" -> False]
Out[12]=

ExpandNonElliptic (2) 

With the setting "ExpandNonElliptic"→False, only Jacobi elliptic functions are expanded out:

In[13]:=
ResourceFunction["EllipticExpand"][ JacobiDN[2 u, m] + JacobiEpsilon[2 u, m], "ExpandNonElliptic" -> False]
Out[13]=

With the setting "ExpandNonElliptic"→True, JacobiEpsilon expressions are also expanded out:

In[14]:=
ResourceFunction["EllipticExpand"][ JacobiDN[2 u, m] + JacobiEpsilon[2 u, m], "ExpandNonElliptic" -> True]
Out[14]=

With the setting "ExpandNonElliptic"→False, only Weierstrass elliptic functions are expanded out:

In[15]:=
ResourceFunction["EllipticExpand"][ WeierstrassP[2 u, {0, -1}] + WeierstrassZeta[2 u, {0, -1}], "ExpandNonElliptic" -> False]
Out[15]=

With the setting "ExpandNonElliptic"→True, WeierstrassZeta expressions are also expanded out:

In[16]:=
ResourceFunction["EllipticExpand"][ WeierstrassP[2 u, {0, -1}] + WeierstrassZeta[2 u, {0, -1}], "ExpandNonElliptic" -> True]
Out[16]=

ExpandWeierstrass (2) 

With the setting "ExpandWeierstrass"→True, Weierstrass elliptic functions are expanded out:

In[17]:=
ResourceFunction[ "EllipticExpand"][{JacobiDC[u - v, m], WeierstrassP[u - v, {g2, g3}]}, "ExpandWeierstrass" -> True]
Out[17]=

With the setting "ExpandWeierstrass"→False, Weierstrass elliptic functions are left untouched:

In[18]:=
ResourceFunction[ "EllipticExpand"][{JacobiDC[u - v, m], WeierstrassP[u - v, {g2, g3}]}, "ExpandWeierstrass" -> False]
Out[18]=

Applications (2) 

Find the addition law for InverseJacobiSN:

In[19]:=
ResourceFunction["EllipticExpand"][ JacobiSN[InverseJacobiSN[w1, m] + InverseJacobiSN[w2, m], m]] /. {JacobiCN[InverseJacobiSN[w_, m_], m_] :> Sqrt[1 - w^2], JacobiDN[InverseJacobiSN[w_, m_], m_] :> Sqrt[1 - m w^2]}
Out[19]=

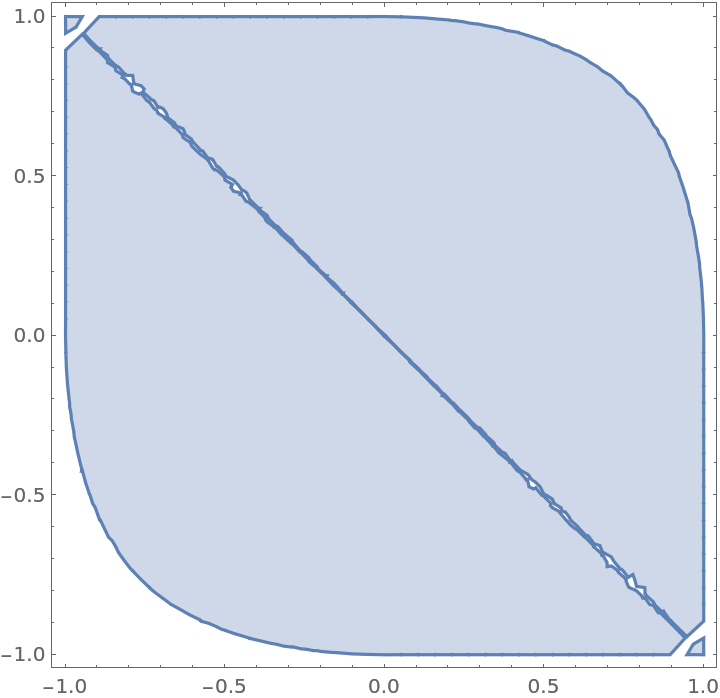
Because of the multivaluedness of InverseJacobiSN, this law does not hold everywhere:

In[20]:=
With[{m = 1/2}, RegionPlot[ InverseJacobiSN[( Sqrt[1 - w1^2] Sqrt[1 - m w1^2] w2 + w1 Sqrt[1 - w2^2] Sqrt[1 - m w2^2])/(1 - m w1^2 w2^2), m] == InverseJacobiSN[w1, m] + InverseJacobiSN[w2, m], {w1, -1, 1}, {w2, -1, 1}]]
Out[20]=
In[21]:=
InverseJacobiSN[( Sqrt[1 - w1^2] Sqrt[1 - m w1^2] w2 + w1 Sqrt[1 - w2^2] Sqrt[1 - m w2^2])/(1 - m w1^2 w2^2), m] - (InverseJacobiSN[w1, m] + InverseJacobiSN[w2, m]) /. {w1 -> 1, w2 -> 1, m -> 1/2}
Out[21]=

Version History

  • 1.0.0 – 14 June 2021

Source Metadata

  • Citation:
    • Carlson B.C., "Symmetry in c, d, n of Jacobian elliptic functions." Journal of Mathematical Analysis and Applications, vol. 299, no. 1, 242–253, 2004. DOI: 10.1016/j.jmaa.2004.06.049
    • "Jacobian Elliptic Functions: Addition Theorems." §22.8 in F. W. J. Olver et al. (eds.), NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov/22.8. Release 1.1.4 of 2021-01-15.
    • "Weierstrass Elliptic and Modular Functions: Addition Theorems and Other Identities." §23.10 in F. W. J. Olver et al. (eds.), NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov/23.10. Release 1.1.4 of 2021-01-15.

Author Notes

Support for expanding WeierstrassSigma, EllipticExp, and EllipticExpPrime will be added in a future version.

License Information