Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ElasticData

Source Notebook

Compute elastic properties of a material with a specified elastic tensor (stiffness matrix)

Contributed by: Wolfram Staff

ResourceFunction["ElasticData"][m]

returns basic elastic properties of a material with the stiffness matrix m.

ResourceFunction["ElasticData"][params]

gives elastic properties corresponding to the specified material parameters params.

ResourceFunction["ElasticData"][params,"prop"]

gives the specified property "prop".

ResourceFunction["ElasticData"][params,{"prop1","prop2",…}]

gives an association of property values.

ResourceFunction["ElasticData"][…,session]

uses the specified running ExternalSessionObject session.

Details and Options

ResourceFunction["ElasticData"] returns a combined association of elastic properties available in the Python packages mechelastic.core.ELATE and mechelastic.core.ElasticProperties.
If the necessary Python dependencies are not installed, the first invocation of ResourceFunction["ElasticData"] can take longer than usual as the function attempts to install the necessay packages automatically, using the the resource function PythonEvaluateWithDependencies.
Should the automatic installation fail for some packages, it might still be possible to install the packages manually using the resource function PythonPackageInstall.
The input stiffness matrix m is also called the elastic tensor.
The specified material parameters params can be one of the following:
{m,atoms,fc,lm}a list of the stiffness matrix m, the list of atoms, their fractional coordinates fc and lattice matrix lm
{m,sassoc}the stiffness matrix m and an association of the structural parameters sassoc
passocparameters given as an association
sassoc must contain the keys "Atoms", "FractionalCoordinates" and "LatticeMatrix" or be given in the form of the "structure" property association as returned by the Function Repository item MaterialsProjectData.
passoc can be given in the form of an association returned by MaterialsProjectData, in which case it must contain the "elasticity" and "structure" properties.
The argument prop can be a string representing one of the available properties: Automatic to give most of the basic properties, Full to give all the available basic properties or All to give an association of most of the basic properties along with the properties corresponding to property plots.
When combining properties obtained from the underlying Python packages, ResourceFunction["ElasticData"][params,Automatic] omits duplicate properties that are available under different names, whereas ResourceFunction["ElasticData"][params,Full] returns all the available basic properties.
For properties corresponding to plots, propi can be given in the form {"namei",opts…}, where opts can be options settings for ListPlot.
ResourceFunction["ElasticData"]["Properties"] gives a list of the available property names.
ResourceFunction["ElasticData"]["PropertyRules"] provides a mapping between the curated property names and the underlying Python-side names.
ResourceFunction["ElasticData"][…,session] avoids the overhead of opening a new Python session for every successive call.
ResourceFunction["ElasticData"] accepts the option "PrintOutput" that controls how the print output from the Python evaluations should be handled:
Trueallow print output
Falsesuppress print output (default)
Automaticpass through print output
ResourceFunction["ElasticData"][…,"PrintOutput"→Automatic] appends the contents of print statements to the returned association in the form "Comments"→comments.

Examples

Basic Examples (2) 

Get the basic properties of the elastic tensor of lithium niobate:

In[1]:=
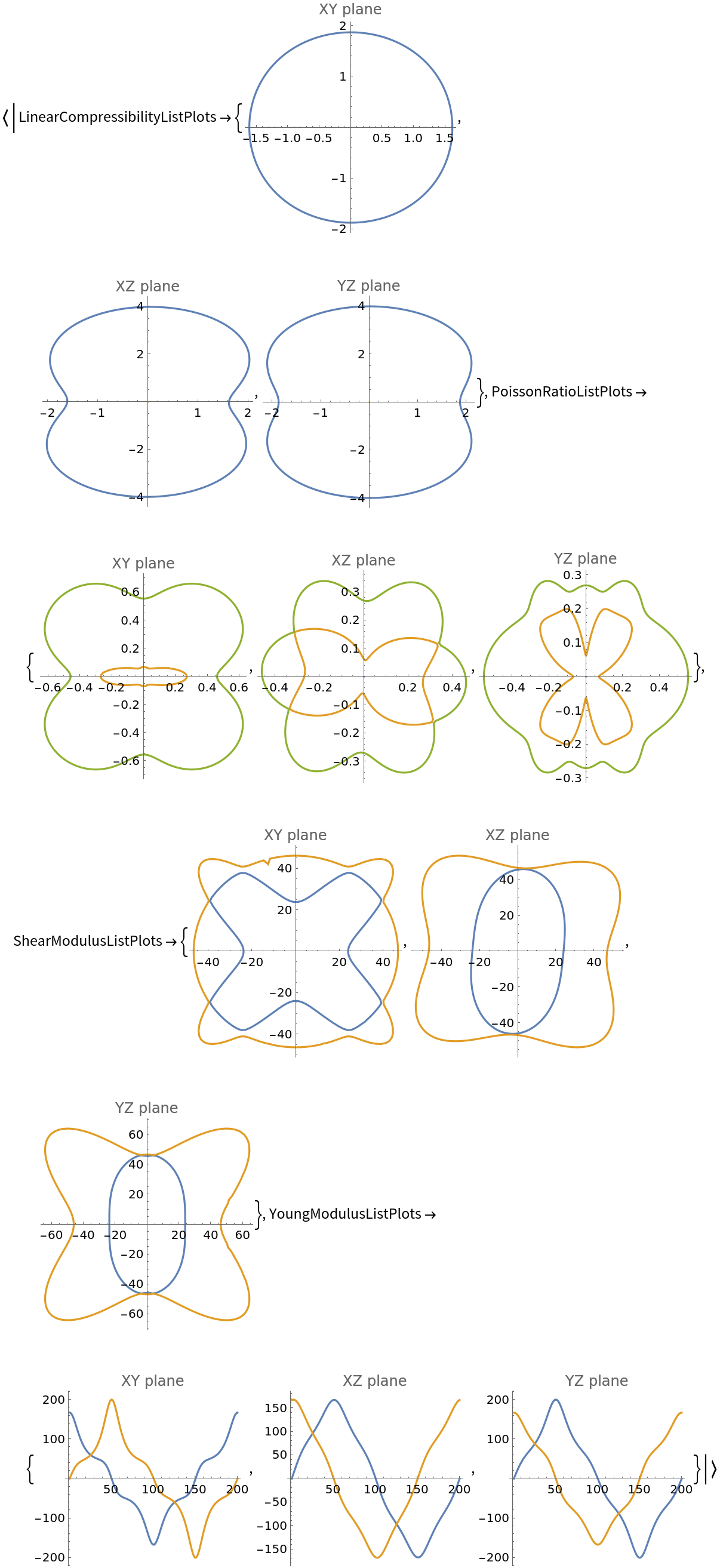
( data = ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}]) // Short
Out[1]=

The available properties:

In[2]:=
Keys[data]
Out[2]=

Create a dataset of the data:

In[3]:=
Dataset[data]
Out[3]=

Plot the spatial dependence of the shear modulus:

In[4]:=
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}, "ShearModulusListPlots"]
Out[4]=

Scope (8) 

Get basic elastic properties of a material:

In[5]:=
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}] // Short
Out[5]=

Get the specified property:

In[6]:=
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}, "MinShearModulus"]
Out[6]=

Several properties:

In[7]:=
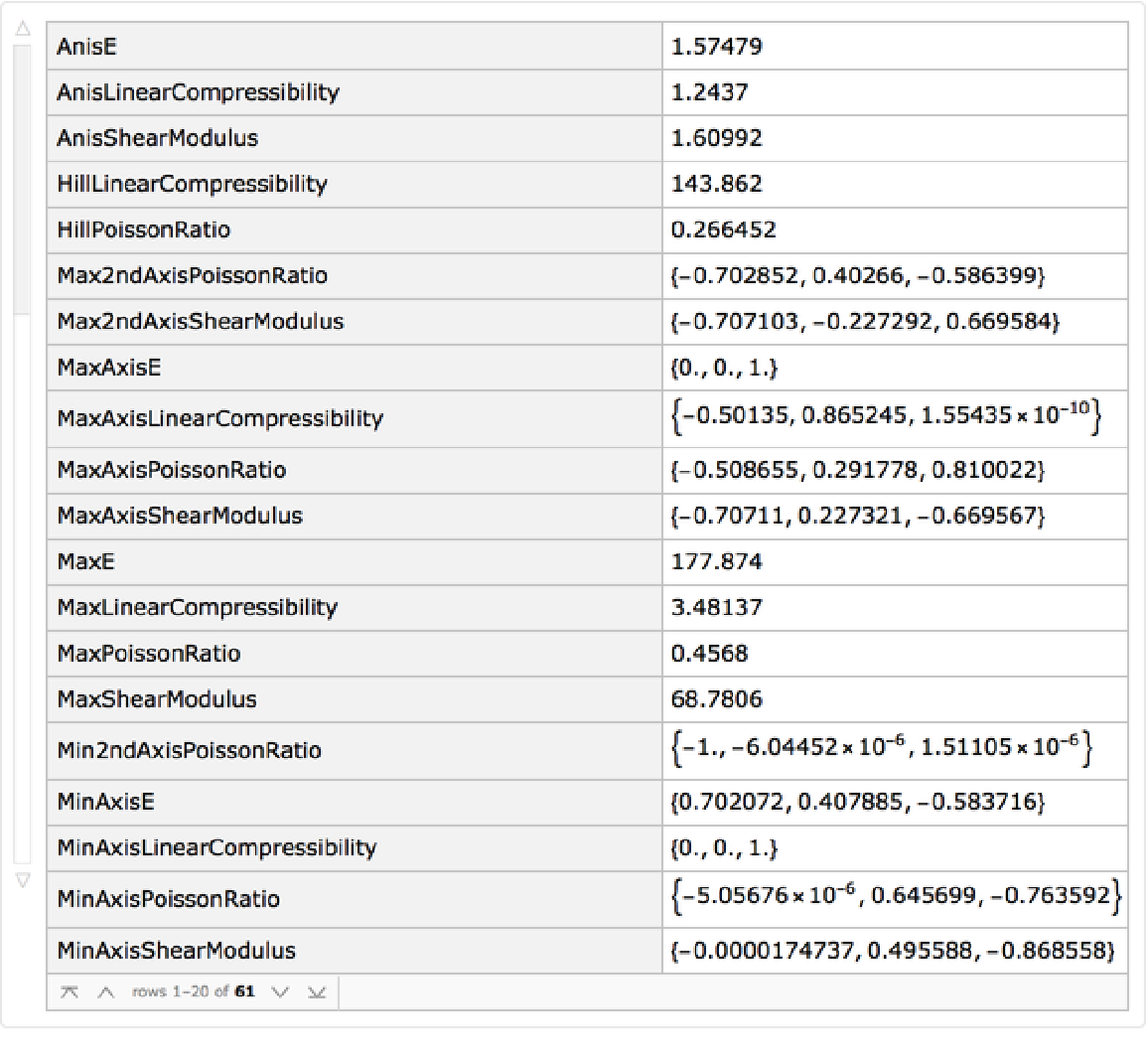
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}, {"MinShearModulus", "MaxShearModulus"}]
Out[7]=

All available properties:

In[8]:=
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}, All]
Out[8]=

Specify plot options:

In[9]:=
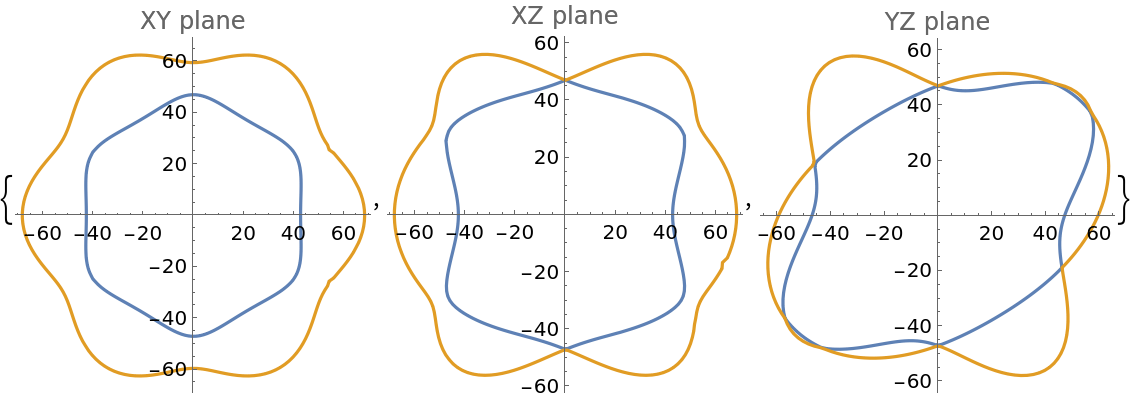
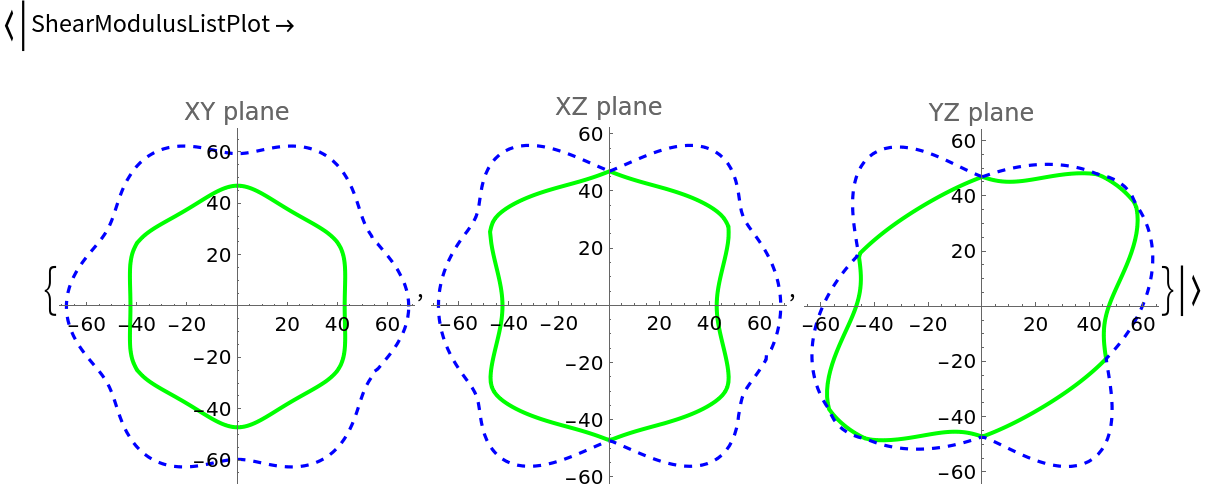
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}, {"ShearModulusListPlots", PlotStyle -> {{Green, Thick}, {Blue, Dashed}}}]
Out[9]=

Obtain elastic properties of TiPbO3 given its elastic tensor and structure properties:

In[10]:=
m = {{173., 79., 46., 0., 0., 0.}, {79., 173., 46., 0., 0., 0.}, {46., 46., 44., 0., 0., 0.}, {0., 0., 0., 35., 0., 0.}, {0., 0., 0., 0., 35., 0.}, {0., 0., 0., 0., 0., 87.}};
In[11]:=
atoms = {"Ti", "Pb", "O", "O", "O"};
In[12]:=
fractionalCoordinates = {{0.5, 0.5, 0.520923}, {0., 0., 0.969212}, {0.5, 0.5, 0.142449}, {0., 0.5, 0.626658}, {0.5, 0., 0.626658}};
In[13]:=
latticeMatrix = {{3.861215, 0., 0.}, {0., 3.861215, 0.}, {0., 0., 4.627061}};
In[14]:=
ResourceFunction[ "ElasticData"][{m, atoms, fractionalCoordinates, latticeMatrix}] // Short
Out[14]=

Obtain the same result by supplying the parameters as a single association or as the elastic tensor and structure properties given as an association:

In[15]:=
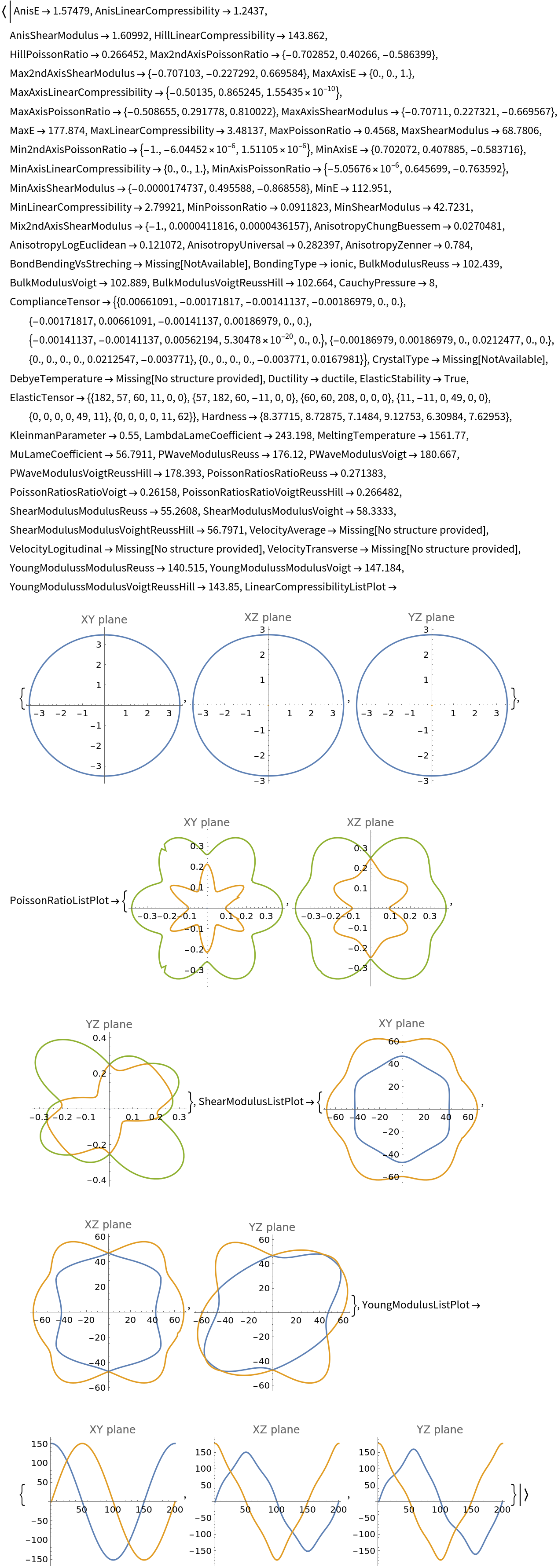
ResourceFunction[ "ElasticData"][<|"ElasticTensor" -> m, "Atoms" -> atoms, "FractionalCoordinates" -> fractionalCoordinates, "LatticeMatrix" -> latticeMatrix|>] === ResourceFunction[ "ElasticData"][{m, <|"Atoms" -> atoms, "FractionalCoordinates" -> fractionalCoordinates, "LatticeMatrix" -> latticeMatrix|>}] === %
Out[15]=

Obtain elastic properties of wüstite taking the elasticity and structure properties from the Materials Project database:

In[16]:=
ResourceFunction["MaterialsProjectData"][ "mp-18905", {"elasticity", "structure"}][[1]] // Short
Out[16]=
In[17]:=
ResourceFunction["ElasticData"][%] // Short
Out[17]=

Make several calls to the function in the same external session:

In[18]:=
session = StartExternalSession["Python"]
Out[18]=
In[19]:=
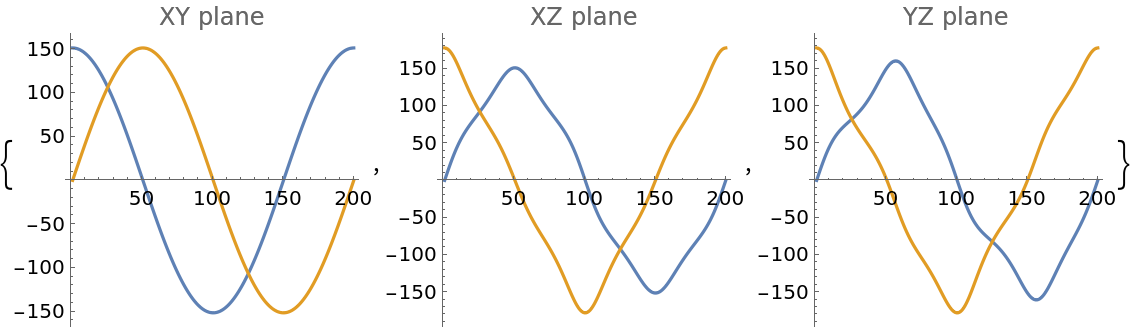
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}, "YoungModulusListPlots", session]
Out[19]=
In[20]:=
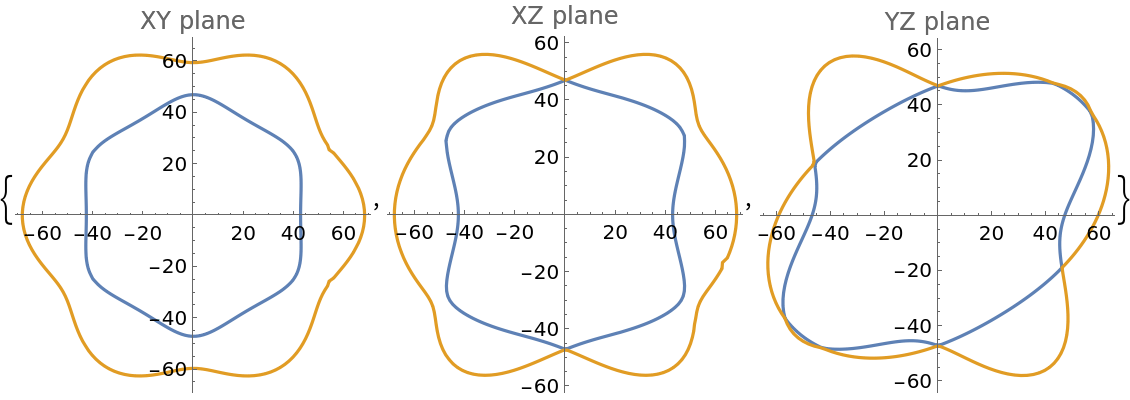
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}, "ShearModulusListPlots", session]
Out[20]=

End the session:

In[21]:=
DeleteObject[session]

Applications (5) 

Plot spatial dependencies of elastic properties of niobium pentoxide. Start a Python session:

In[22]:=
session = StartExternalSession["Python"]
Out[22]=

Obtain the elastic tensor of niobium pentoxide from the Materials Project database:

In[23]:=
m = First[ Flatten[Values[ ResourceFunction["MaterialsProjectData"]["mp-1595", "elasticity", session]]]]["elastic_tensor"]
Out[23]=

Available elastic property plots:

In[24]:=
Cases[ ResourceFunction["ElasticData"]["Properties", session], _?(StringContainsQ[#, "Plots"] &)]
Out[24]=

Plot spatial dependencies:

In[25]:=
ResourceFunction["ElasticData"][m, %, session]
Out[25]=

End session:

In[26]:=
DeleteObject[session]

Properties and Relations (3) 

Currently available elastic properties:

In[27]:=
ResourceFunction["ElasticData"]["Properties"]
Out[27]=

A mapping between the curated property names and the Python-side names:

In[28]:=
ResourceFunction["ElasticData"]["PropertyRules"]
Out[28]=

Elastic properties that are available in the Materials Project database can be obtained with the resource function MaterialsProjectData:

In[29]:=
ResourceFunction["MaterialsProjectData"]["mp-2593", "elasticity"]
Out[29]=

Possible Issues (2) 

On macOS, the installation of the underlying MechElastic Package in the system Python may fail:

In[30]:=
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}]
Out[30]=
In[31]:=
ResourceFunction["FindPythonExecutable"][]
Out[32]=

Use a Python version installed with Homebrew, for instance using pyenv:

In[33]:=
RegisterExternalEvaluator["Python", "/Users/admin/.pyenv/shims/python"]
Out[33]=
In[34]:=
ResourceFunction[ "ElasticData"][{{182, 57, 60, 11, 0, 0}, {57, 182, 60, -11, 0, 0}, {60, 60, 208, 0, 0, 0}, {11, -11, 0, 49, 0, 0}, {0, 0, 0, 0, 49, 11}, {0, 0, 0, 0, 11, 62}}] // Short
Out[34]=

Some elastic properties are not available from the stiffness matrix alone:

In[35]:=
m = {{173., 79., 46., 0., 0., 0.}, {79., 173., 46., 0., 0., 0.}, {46., 46., 44., 0., 0., 0.}, {0., 0., 0., 35., 0., 0.}, {0., 0., 0., 0., 35., 0.}, {0., 0., 0., 0., 0., 87.}};
In[36]:=
ResourceFunction["ElasticData"][m, "DebyeTemperature"]
Out[36]=

Provide additional structure data to obtain the property:

In[37]:=
atoms = {"Ti", "Pb", "O", "O", "O"};
In[38]:=
fractionalCoordinates = {{0.5, 0.5, 0.520923}, {0., 0., 0.969212}, {0.5, 0.5, 0.142449}, {0., 0.5, 0.626658}, {0.5, 0., 0.626658}};
In[39]:=
latticeMatrix = {{3.861215, 0., 0.}, {0., 3.861215, 0.}, {0., 0., 4.627061}};
In[40]:=
ResourceFunction[ "ElasticData"][{m, atoms, fractionalCoordinates, latticeMatrix}, "DebyeTemperature"]
Out[40]=

Version History

  • 1.0.0 – 29 June 2021

Related Resources

Author Notes

Tested on macOS with Python 3.7.3 and 3.8.6 and Windows with Python 3.8.9. MechElastic does not seem to install properly with 3.9 (April 2021).
Only top-level ELATE and ElasticProperties and functions are supported at this time.
Property names need further curation.
Access to the following ELATE properties are not yet implemented:
"anis_Poisson" and "anix_Poisson", which need a bit of special treatment as ELATE gives one or the other
properties along the lines of "obj.x if hasattr(obj, 'x') else 'missing'", which need a bit of massaging on the Wolfram Language side too
all 3D plots
From ElasticProperties, "structure" is not currently returned.
Eventually, we might want to be able to:
accept crit for MaterialsProjectData
accept SymmetrizedArray objects for the elastic tensor as input
accept optional n-points in sampled plots ("*Plots")
pass different options to plots within the same group, e.g. ElasticData[m,{"ShearPlot",{Background→Yellow,AspectRatio→2} ,Background→Red,…}]
The option "NameSubstitutions" (from PythonEvaluateWithDependencies) should probably remain undocumented. It's here only as a precaution for the case when the underlying Python packages release an incompatible update and we have not caught up yet. Users should then be able to tweak the installed packages themselves.
As a wrapper to the mechelastic.core.ELATE package, the current implementation gives numeric/sampled results. It may be worthwhile to also provide symbolic results, as appropriate, based particularly on the original Wolfram Language implementation in https://aip.scitation.org/doi/suppl/10.1063/1.4802770/suppl_file/analysis_code.zip.
Uses MechElastic package for off-line calculations. Conceivably can use REST interface directly as an option.

License Information