Details
The ring of Eisenstein integers is ℤ[
ω], where
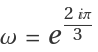
is a primitive third root of unity.
ResourceFunction["EisensteinIntegers"] supports two representations: an Eisenstein integer can be given either as a pair
{i1,i2}, which denotes
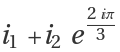
, or as
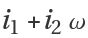
. In the latter case, the symbol used to denote the extension element,
ω, must be given explicitly in all operations.
The norm of an Eisenstein integer is defined as the product of the integer with its complex conjugate. The conjugate of
ω is
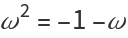
.
There are six units in the ring of Eisenstein integers: {±1,±ω,±ω2=∓(1+ω)}. An Eisenstein integer is a unit if and only if its norm is 1.
Supported unary operations are "Re", "Im", "ReIm", "Conjugate", "Norm", "Abs", "Reciprocal", "UnitQ", "PrimeQ" and "FactorInteger".
The conjugate of ω is ω2. This is equal to -1-ω due to the fundamental identity ω2+ω+1=0. ResourceFunction["EisensteinIntegers"] always reduces by this identity, so ω2 is never used in a result (and is not supported in input).
Supported binary operations are "Plus", "Times", "Power", "Dot", "Quotient", "Remainder", "QuotientRemainder", "AssociatesQ", "DividesQ","IntegerExponent", "GCD" and "ExtendedGCD".
Except where specified otherwise, all supported operations in effect do what the corresponding functions do with ordinary or Gaussian integers.
ResourceFunction["EisensteinIntegers"] supports "Power" when the second argument is an explicit nonnegative integer.
Ordinary multiplication is used in "Dot", that is, no conjugation takes place.
ResourceFunction["EisensteinIntegers"] also supports "ListPlus" and "ListTimes" so one can give a list of arguments for adding or multiplying.
ResourceFunction["EisensteinIntegers"] also supports "PowerMod". The power must be a nonnegative integer. The modulus must be an Eisenstein integer.
ResourceFunction["EisensteinIntegers"] regards the multiplier of the extension element as the "imaginary" part, even though it has both a real and an imaginary component in the complex plane.
The Eisenstein integer a+b ω has norm a2+b2-ab. The absolute value is the square root of the norm.
Unary operations and binary operations that do not use division allow symbolic input—that is, Eisenstein numbers that are not expressed using explicit integers.
The reciprocal operation will in general return an Eisenstein rational rather than an integer. All other operations return integers when given explicit Eisenstein integer inputs.
![e0 = 3 + 7 w;
e1 = 2 - 7 w;
eprod = ResourceFunction["EisensteinIntegers"][e0, e1, w, "Times"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/6fcfc08d5e2ede89.png)
![e0 = 3 + 7 w;
e1 = ResourceFunction["EisensteinIntegers"][e0, 4 + 5 w, w, "Times"];
e2 = ResourceFunction["EisensteinIntegers"][e0, 6 - 7 w, w, "Times"];
g = ResourceFunction["EisensteinIntegers"][e1, e2, w, "GCD"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/1a1f4fe220680744.png)
![SeedRandom[1234];
enums = RandomInteger[{-5, 5}, {16, 2}];
eprims = Select[enums, ResourceFunction["EisensteinIntegers"][#, "PrimeQ"] &]](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/1b505b873e72e74e.png)
![Table[ResourceFunction["EisensteinIntegers"][eprims[[i]], eprims[[j]],
"AssociatesQ"], {i, Length[eprims] - 1}, {j, i + 1, Length[eprims]}] // Flatten](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/1d8ca113857818ee.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9cdc71b5-7ff3-427e-bcab-ffb73207ea80"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/0be40adfe92b770d.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/e2593eb2-8fa1-4441-90d8-dad97f8e723a"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/722c443ae39c0d19.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/284cccfd-853a-411b-83f1-c7f538dfc27c"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/15b00cb1d429a6d5.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/bea72e8a-276f-44cb-9277-aecc98f4175f"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/625c01963efeb97a.png)
![Graphics[RegularPolygon[ReIm[#], {1/2, \[Pi]/2}, 6] & /@ Table[ResourceFunction["EisensteinIntegers"][7/6 + \[Omega], n, \[Omega], "Power"], {n, 18}] /. \[Omega] -> Exp[2 Pi I/3]]](https://www.wolframcloud.com/obj/resourcesystem/images/9e4/9e44399a-4f41-4fc9-a331-18f9f46c9889/0c844e79e53a4ee3.png)
