Function Repository Resource:

EisensteinFactorInteger

Source Notebook

Factor an integer into powers of Eisenstein primes

Contributed by: Daniel Lichtblau

ResourceFunction["EisensteinFactorInteger"][n]

gives a list of the Eisenstein prime factors of n, together with their exponents.

ResourceFunction["EisensteinFactorInteger"][n,ω]

returns a result using ω to denote the Eisenstein unit .

Details

Eisenstein integers are elements of the ring

where

is a primitive third root of unity.

The element defining the algebraic extension can also be written as

The Eisenstein integers are the algebraic integers in the number field

, which is sometimes referred to as the third cyclotomic field.

The result of ResourceFunction["EisensteinFactorInteger"] is unique up to multiplying factors by units (so the Eisenstein integers are a unique factorization domain).

The units in the ring of Eisenstein integers are {±1,±ω,±ω²}.

ResourceFunction["EisensteinFactorInteger"] initially factors its input into ordinary prime factors.

Integer primes of the form 6m+1, along with 3, can be further factored into a product of Eisenstein primes.

Integer primes of the form 6m-1 are also Eisenstein primes.

ResourceFunction["EisensteinFactorInteger"] will also factor rationals over the Eisenstein integers, using negative integer powers for the denominator factors.

ResourceFunction["EisensteinFactorInteger"] in effect solves the generalized Pell equation n=a²+3b², using Cornacchia's algorithm.

Examples

Basic Examples (2)

Factor 171 over the Eisenstein integers:

In[1]:=

Out[1]=

Check the result:

In[2]:=

Out[2]=

Scope (3)

Factor a rational over the Eisenstein integers:

In[3]:=

$fracfacs = ResourceFunction["EisensteinFactorInteger"][171/181]$

Out[3]=

Check the result:

In[4]:=

$Times @@ (Power @@@ fracfacs) // RootReduce$

Out[4]=

Use a symbol to denote the Eisenstein unit :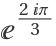

In[5]:=

$ResourceFunction["EisensteinFactorInteger"][171, \[Omega]]$

Out[5]=

Primes of the form 6k+1 factor further in the Eisenstein ring:

In[6]:=

Out[6]=

Primes of the form 6k-1 will not factor further:

In[7]:=

Out[7]=

Possible Issues (1)

EisensteinFactorInteger does not attempt to factor non-integer elements in the Eisenstein ring:

In[8]:=

Out[8]=

Neat Examples (12)

Factoring Eisenstein integers can be done as follows: (1) Compute the norm (an ordinary integer). (2) Factor the norm over the Eisenstein integers. (3) Use division to determine, for each pair of conjugate Eisenstein primes in the norm factorization, which divides the original Eisenstein integer. (4) Determine the correct exponent for each such factor. (5) Determine the appropriate Eisenstein unit that makes the factorization correct.

Step (3) requires modification when 3 divides the norm. The (4) involves a subtlety: Since different Eisenstein primes can have the same norm, one cannot assume that the exponents for prime factors in step (2) will be correct for the Eisenstein primes retained in step (3). We work with examples that have exponent of 1 and hence cannot exhibit this pathology.

Define the Eisenstein norm (n(i+j ω)=i²-i j+j²):

In[9]:=

Compute the norm of 8+17ω:

In[10]:=

Out[10]=

Factor the norm:

In[11]:=

Out[11]=

Use GroebnerBasis and PolynomialReduce to provide a divisibility test for Eisenstein integers:

In[12]:=

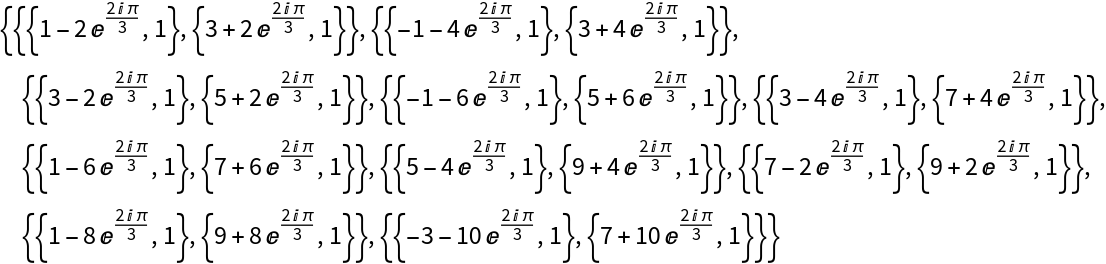
$EisensteinDividesQ[i1_, i2_, w_] := With[ {gb = GroebnerBasis[{i1, w^2 + w + 1}, w, CoefficientDomain -> Integers]}, PolynomialReduce[i2, gb, w, CoefficientDomain -> Integers][[2]] == 0]$

Determine which Eisenstein prime factors of 129 are actually factors of 8+13ω:

In[13]:=

Out[13]=

Find the unit factor:

In[14]:=

$findUnit[facs_, eint_, w_] := Module[ {redprod, a, b, c, pred, sv}, redprod = PolynomialMod[Times @@ (facs[[All, 1]]^facs[[All, 2]]), w^2 + w + 1]; pred = PolynomialReduce[(a + b*w + c*w^2)*redprod - eint, w^2 + w + 1, {w, a, b, c}]; sv = SolveAlways[{pred[[2]] == 0, a*b == 0, b*c == 0, a*c == 0}, w]; {a, b, c} . {1, w, w^2} /. sv[[1]] /. Thread[{a, b, c} -> 0] ] unitfac = findUnit[actualFactors, eint, w]$

Out[14]=

Check the factorization:

In[15]:=

Out[15]=

When 3 divides the norm, we can use either Eisenstein prime factor of 3 for our final result:

In[16]:=

eint = 8 + 13 w;
enorm = EisensteinNorm[eint, w];
{enorm, IntegerQ[enorm/3]}

Out[16]=

Compute the factors:

In[17]:=

Out[17]=

Compute the associated unit:

In[18]:=

Out[18]=

Check the result:

In[19]:=

Out[19]=

Show that we get an equally valid prime factorization from using the other prime factor of 3:

In[20]:=

$facs = Prepend[ ResourceFunction["EisensteinFactorInteger"][enorm/3, w], {2 + w, 1}]; actualFactors = Pick[facs, Map[EisensteinDividesQ[#, eint, w] &, facs[[All, 1]]]]; unitfac = findUnit[actualFactors, eint, w]; {unitfac, actualFactors, PolynomialMod[(Times @@ (actualFactors[[All, 1]]^ actualFactors[[All, 2]]))*unitfac - eint, w^2 + w + 1]}$

Out[20]=

A full implementation that properly handles all the steps indicated above may be found in the much larger resource function EisentsteinIntegers.

Version History

1.0.0 – 05 April 2021

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

EisensteinFactorInteger

Details