Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EinsteinSolid

Source Notebook

Make a simulation of the Einstein solid

Contributed by: Enrique Zeleny

ResourceFunction["EinsteinSolid"][array,steps]

makes a simulation of the Einstein solid starting with array and using steps iterations.

Details and Options

At low temperatures, the Dulong–Petit law fails and the specific heat capacity at constant volume CV of solids is no longer constant. The Einstein quantum model for a solid correctly explains this phenomenon. We can make a simplified model of a solid with a 2D cell array (Black and Ogborn, 1976) with one oscillator in each cell with an energy of a multiple of ℏ ω, and thermal interaction reproduced through a transfer of a quantum of energy between a pair of these cells chosen randomly.

Examples

Basic Examples (2) 

The initial state assigns one quantum to every cell. After about 1,000 steps, the distribution of a thermal equilibrium state and Boltzmann distribution is obtained; it is stable after more steps:

In[1]:=
ResourceFunction["EinsteinSolid"][ConstantArray[1, {16, 16}], 1000]
Out[1]=

Plot the results:

In[2]:=
ArrayPlot[%]
Out[2]=
In[3]:=
BarChart[Reverse[Sort[Counts[Flatten[%%]]]]]
Out[3]=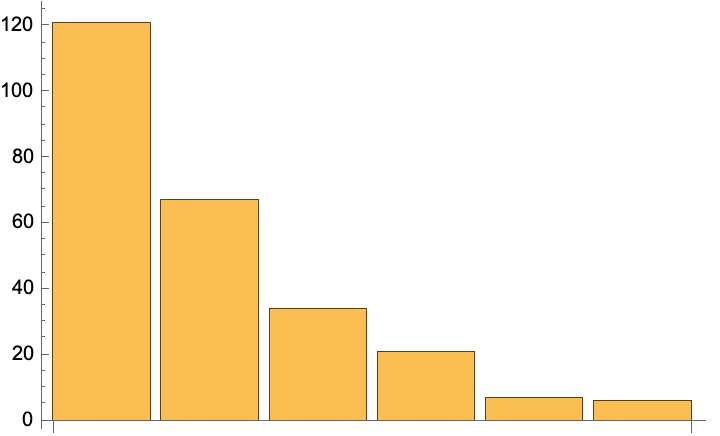

After about 20,000 steps, the distribution of energies closely approximates the Boltzmann distribution, and thermal equilibrium is obtained:

In[4]:=
results = ResourceFunction["EinsteinSolid"][ConstantArray[1, {16, 16}], 20000];
In[5]:=
data = Count[results, #, {2}] & /@ Range[0, 12]
Out[5]=

The left chart represents instantaneous values m(ε), the right chart represents the mean values given by the canonical distribution (equal to ) and the red curve represents the fit of the occupancies:

In[6]:=
RectangleChart[{Transpose[{Table[1, {13}], data}], Table[{1, 128 2^-\[Nu]}, {\[Nu], 0, 12}]}]
Out[6]=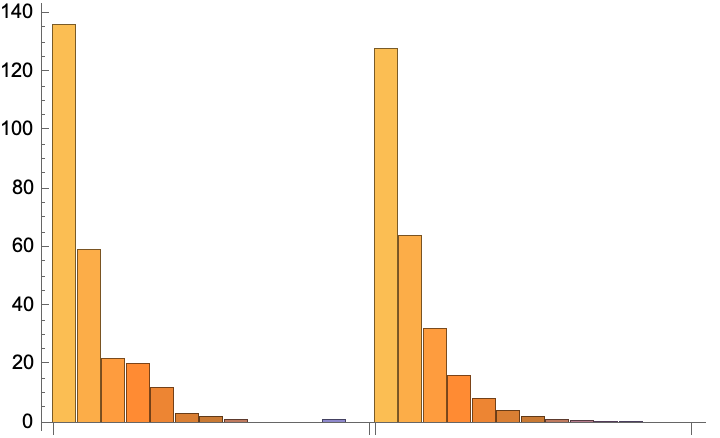

Fitting data:

In[7]:=
With[{fit = Fit[Transpose@{Range[0, 12], data}, {2^(-\[Nu])}, \[Nu]]}, Show[RectangleChart[Transpose[{Table[1, {13}], data}]], Plot[Evaluate[fit], {\[Nu], 0, Length[data]}, PlotStyle -> Red, PlotRange -> All], PlotLabel -> Row[List @@ fit, "\[Times]"]]]
Out[7]=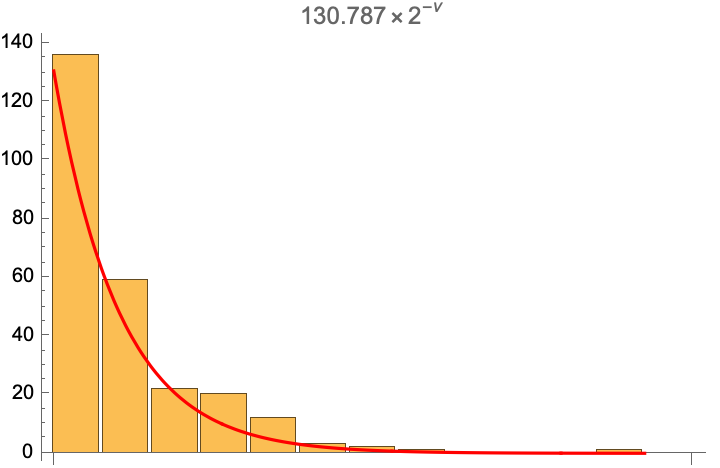

The number of points assigned to each cell is the number of quanta possessed by the oscillator (occupancy):

In[8]:=
Grid[{Prepend[Range[0, Length[data] - 1], "energy"], Prepend[data, "occupancy"]}, Background -> LightYellow, Dividers -> {All, All}, ItemSize -> {{5, {2}}}]
Out[8]=

Requirements

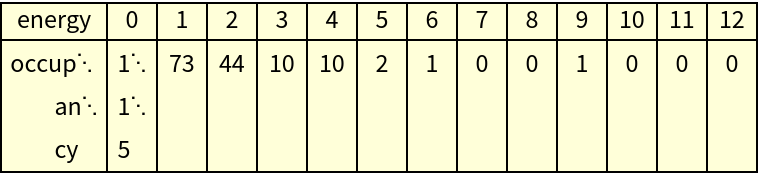Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 25 February 2019

License Information