Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EgyptianFraction

Source Notebook

Compute Egyptian fractions using different methods

Contributed by: David Eppstein

ResourceFunction["EgyptianFraction"][fraction]

gets Egyptian fractions from fraction using different methods.

Details and Options

Egyptian fractions give a fraction represented as a sum of fractions with numerator one.
Methods available include "Greedy", "Harmonic", "Odd Greedy", "Pairing", "Splitting", "Binary", "BinaryRemainder", "ContinuedFraction", "GroupedContinuedFraction" and "Hybrid".

Examples

Basic Examples (3) 

Compute the Egyptian fractions for any fraction:

In[1]:=
ResourceFunction["EgyptianFraction"][16/77]
Out[1]=

Check the result:

In[2]:=
Plus @@ ResourceFunction["EgyptianFraction"][16/77]
Out[2]=

Display the result as a sum:

In[3]:=
Row[ResourceFunction["EgyptianFraction"][16/77], "+"]
Out[3]=

Options (9) 

Method (9) 

The method "Harmonic":

In[4]:=
ResourceFunction["EgyptianFraction"][16/77, Method -> "Harmonic"]
Out[4]=

The method "OddGreedy":

In[5]:=
ResourceFunction["EgyptianFraction"][4/81, Method -> "OddGreedy"]
Out[5]=

The method "Pairing":

In[6]:=
ResourceFunction["EgyptianFraction"][18/23, Method -> "Pairing"]
Out[6]=

The method "Splitting":

In[7]:=
ResourceFunction["EgyptianFraction"][5/6, Method -> "Splitting"]
Out[7]=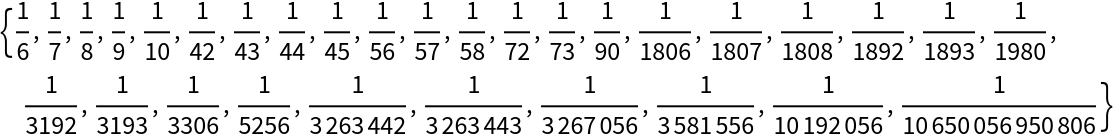

The method "Binary":

In[8]:=
ResourceFunction["EgyptianFraction"][8/453, Method -> "Binary"]
Out[8]=

The method "BinaryRemainder":

In[9]:=
ResourceFunction["EgyptianFraction"][5/7841, Method -> "BinaryRemainder"]
Out[9]=

The method "ContinuedFraction":

In[10]:=
ResourceFunction["EgyptianFraction"][47/59, Method -> "ContinuedFraction"]
Out[10]=

The method "GroupedContinuedFraction":

In[11]:=
ResourceFunction["EgyptianFraction"][31/311, Method -> "GroupedContinuedFraction"]
Out[11]=

The method "Hybrid":

In[12]:=
ResourceFunction["EgyptianFraction"][31/311, Method -> "Hybrid"]
Out[12]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 19 February 2019

License Information