Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EconomizedRationalApproximation

Source Notebook

Find an economized rational approximation to a function

Contributed by: Wolfram Research

ResourceFunction["EconomizedRationalApproximation"][expr,{x,{x0,x1},m,n}]

gives the economized rational approximation to expr that is good over the interval x0 to x1, with numerator order m and denominator order n.

Details and Options

ResourceFunction["EconomizedRationalApproximation"] finds the Padé approximant about the midpoint of the interval x0 to x1, and then perturbs the approximant with Chebyshev polynomials to reduce the leading coefficient in the error.
The Wolfram Language can find the economized rational approximant over the interval x0 to x1 only when it can evaluate power series at the midpoint of the interval.
ResourceFunction["EconomizedRationalApproximation"] produces a ratio of ordinary polynomial expressions, not a special SeriesData object.

Examples

Basic Examples (2) 

Economized rational approximation of degree (2,4) of ⅇx over the interval 0≤x≤2:

In[1]:=
ResourceFunction["EconomizedRationalApproximation"][ E^x, {x, {0, 2}, 2, 4}]
Out[1]=

The difference between the true function and the approximation:

In[2]:=
Plot[% - E^x, {x, 0, 2}]
Out[2]=

Properties and Relations (2) 

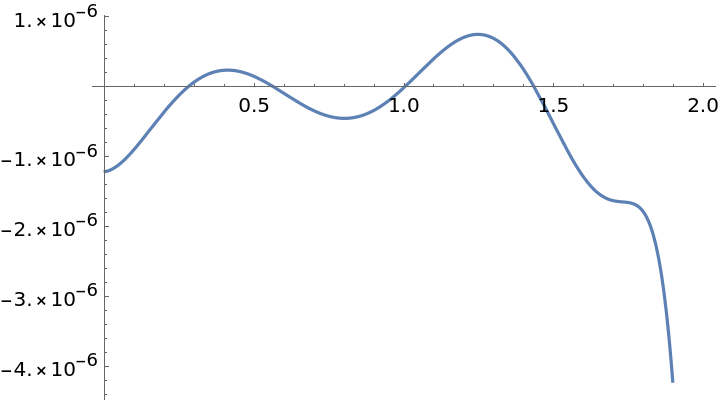Padé approximation is potentially more accurate near the center of the approximation interval:

In[3]:=
f[x] := E^x
In[4]:=
pd = PadeApproximant[f[x], {x, 1, {2, 4}}] // Simplify
Out[4]=
In[5]:=
era = ResourceFunction["EconomizedRationalApproximation"][ f[x], {x, {0, 2}, 2, 4}] // Simplify
Out[5]=
In[6]:=
f[x] - {pd, era} /. x -> 1.1
Out[6]=

But less accurate at the ends:

In[7]:=
N[(pd - f[x])/(era - f[x]) /. {{x -> 0}, {x -> 2}}]
Out[7]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 28 March 2019

Related Resources

License Information