Basic Examples (1) 

The dual Zeckendorf representation of first 20 integers (OEIS: A104326):

In[1]:=

Out[1]=

In[2]:=

Out[2]=

Scope (5) 

By definition, one can directly find dual Zeckendorf representation by eliminating binary string with "00":

In[3]:=

Out[3]=

Recover a number from its dual representation:

In[4]:=

Out[4]=

In[5]:=

Out[5]=

In[6]:=

Out[6]=

In[7]:=

Out[7]=

In the dual representation, the largest index of Fibonacci number has the following property:

In[8]:=

Out[9]=

In[10]:=

Out[10]=

Thus input falls precisely the gap between the sum of F_i for i = 2 to 28 and from 2 to 29=28+1:

In[11]:=

Out[11]=

The second largest value, 26, is found in the similar way by definition:

In[12]:=

Out[12]=

For any input n, its dual Zeckendorf representation is {1,1, … ,1} or zero-free if and only if n= F_k-2, where F_k is the k-th item in regular Fibonacci sequence with k>=4:

In[13]:=

Out[13]=

For any input n, its dual Zeckendorf representation is {1,0,1,0 … ,0|1} or alternating pattern (the ending in 0 or 1 depends on the parity of bit length) if and only if n= F_k-1, where F_k is the k-th item in regular Fibonacci sequence with k>=4:

In[14]:=

Out[14]=

Properties and Relations (3) 

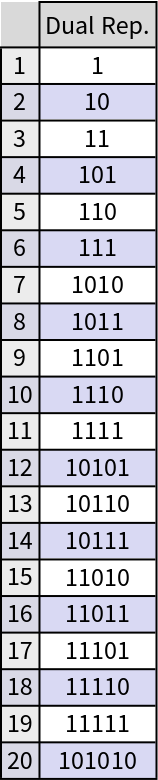
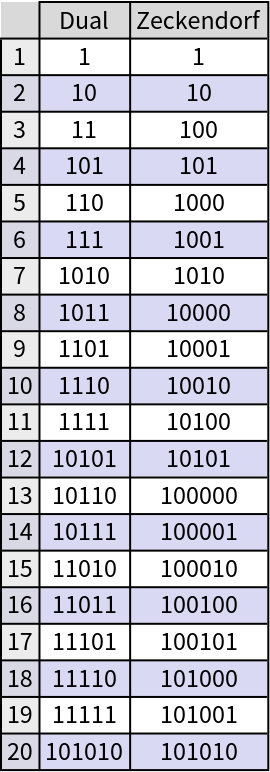
The dual Zeckendorf representation vs. Zeckendorf representation: the former does not allow consecutive zeros, meanwhile the latter does not allow consecutive ones. Check the fact with the first twenty numbers:

In[15]:=

In[16]:=

In[17]:=

Out[17]=

Fibonacci terms minus one:

In[18]:=

Out[18]=

The identical representations for 4, 7, 12, 20, ..., continue:

In[19]:=

Out[19]=

Possible Issues (1) 

The input must be a positive integer. Otherwise the function returns unevaluated:

In[20]:=

Out[20]=

Neat Examples (2) 

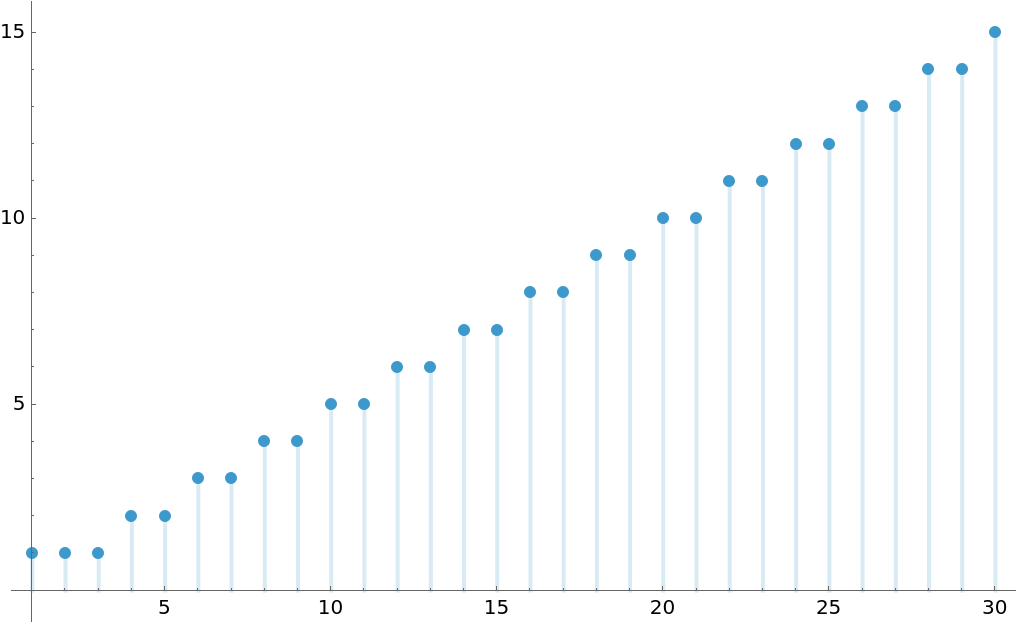
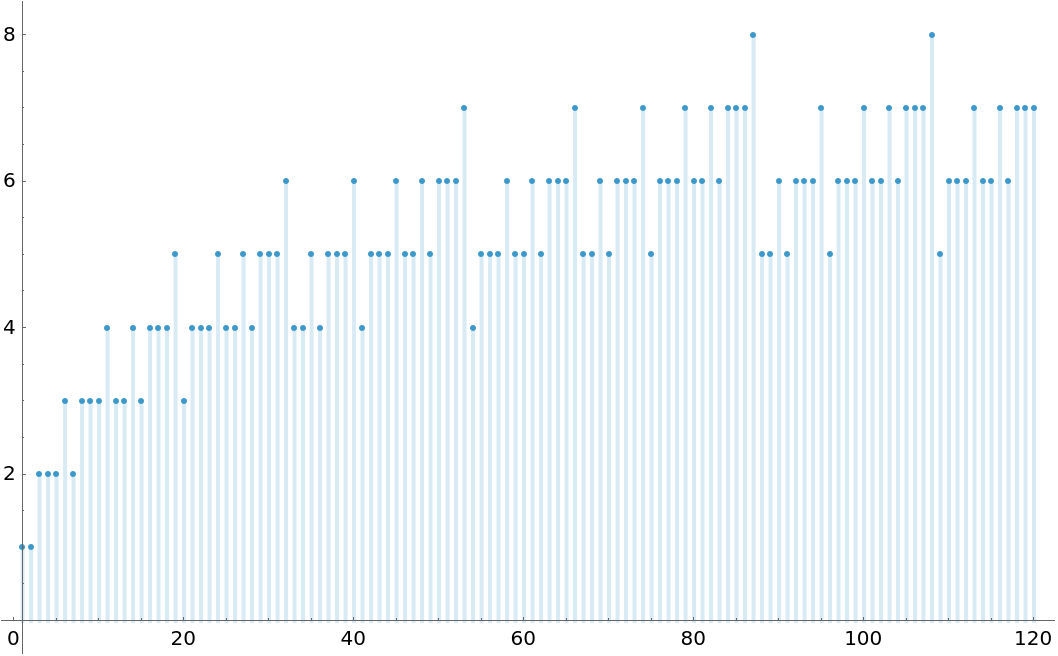
The number of ones in the dual Zeckendorf representation for first 120 numbers:

In[21]:=

Out[21]=

Compare the ones in the Zeckendorf and the dual representation for Fibonacci numbers:

In[22]:=

Out[22]=

In[23]:=

Out[23]=

Visualize the number of ones in the dual representation for Fibonacci number:

In[24]:=

Out[24]=

In[25]:=

Out[25]=

The sequence is OEIS A065033:

In[26]:=

Out[27]=

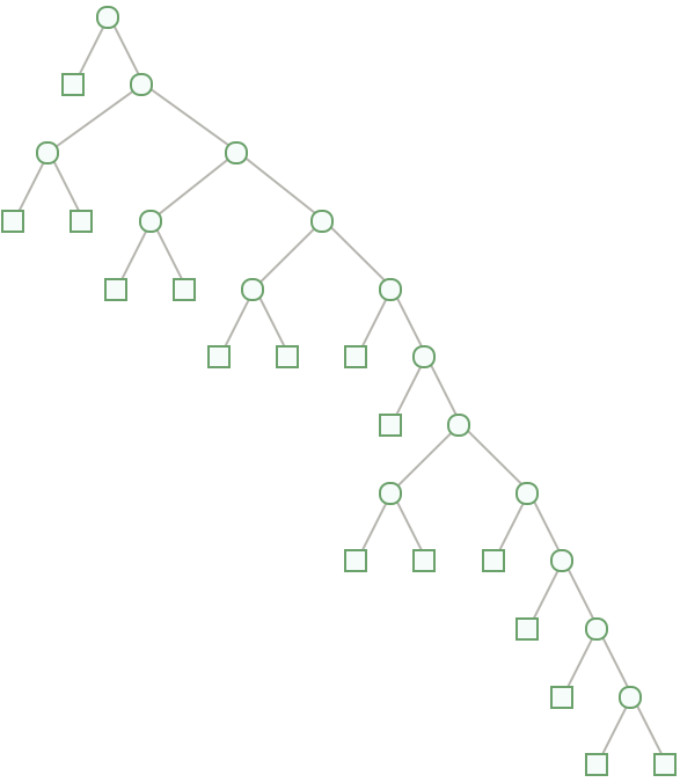
Because no consecutive zeros are allowed, all dual Zeckendorf representations are compact Huffman code:

In[28]:=

Out[28]=

In[29]:=

Out[29]=