Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DoyleSpiral

Source Notebook

Plot Doyle spirals

Contributed by: Dieter Steemann

ResourceFunction["DoyleSpiral"][p,q]

plots Doyle spirals for values p spiral arms and q circles per spiral revolution.

Details and Options

Doyle spirals are special logarithmic spirals of touching circles in which every circle is surrounded by a corona of six touching circles. A linear fractional transformation (or Möbius transformation) is applied to map such spirals (in particular, circle packings) into double spirals.
A logarithmic spiral starts at the origin and winds around the origin at an ever-increasing distance. The Möbius transformation z→(z-1)/(z+1) maps the points (0,1,∞) of the real axis of the complex plane to the points (-1,0,1) on the real axis. Because Möbius transformations preserve circles, the result is a new circle packing in the shape of a double spiral centered at +1 and -1 on the real axis.
"GraphicType" can be any of:
"Basic"a spiral with parameters P and Q
"Moebius"a basic spiral under Möbius transformation
"PQGraph"a spiral with elements along the P- and Q-axes in basic spiral

Examples

Basic Examples (1) 

Plot a Doyle spiral:

In[1]:=
ResourceFunction["DoyleSpiral"][7, 25]
Out[1]=

Options (5) 

ColorFunction (1) 

Add a gradient for ColorFunction:

In[2]:=
ResourceFunction["DoyleSpiral"][2, 25, ColorFunction -> "ThermometerColors"]
Out[2]=

GraphicType (2) 

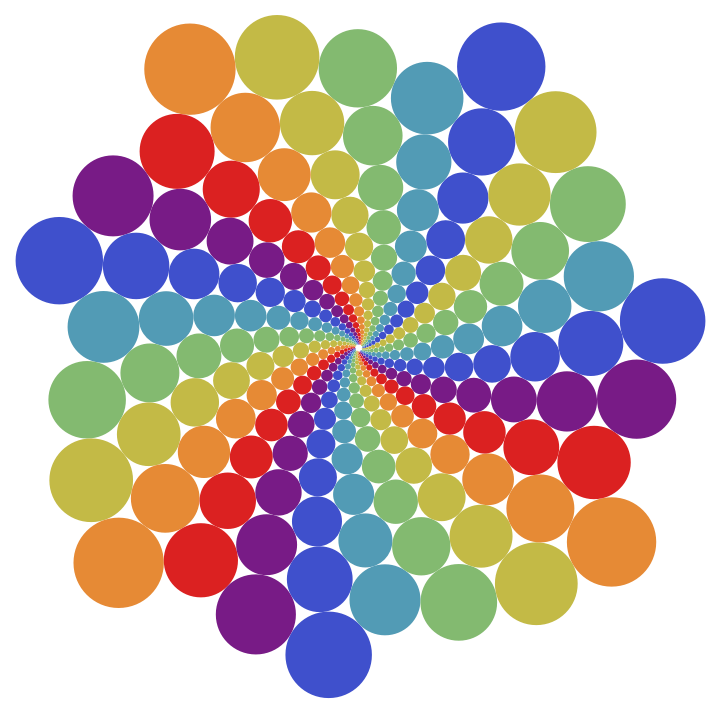Use "GraphicType"→"Moebius":

In[3]:=
ResourceFunction["DoyleSpiral"][2, 25, "GraphicType" -> "Moebius", "Type" -> "Q"]
Out[3]=

Use "GraphicType"→"PQGraph":

In[4]:=
ResourceFunction["DoyleSpiral"][4, 30, "GraphicType" -> "PQGraph"]
Out[4]=

PlotStyle (1) 

Add style directives:

In[5]:=
ResourceFunction["DoyleSpiral"][4, 30, "GraphicType" -> "Moebius", PlotStyle -> {Thick, EdgeForm[Black]}]
Out[5]=

Type (1) 

Compare and contrast the possible options for "Type":

In[6]:=
ResourceFunction["DoyleSpiral"][7, 25, "GraphicType" -> "Moebius", "Type" -> "P"]
Out[6]=
In[7]:=
ResourceFunction["DoyleSpiral"][7, 25, "GraphicType" -> "Moebius", "Type" -> "Q"]
Out[7]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 29 March 2019

Source Metadata

  • Citation:
    • [1] D. Mumford, C. Series and D. Wright, Indra's Pearls: The Vision of Felix Klein, Cambridge: Cambridge University Press, 2006 pp. 62.
      [2] J. Leys, "Hexagonal Circle Packings and Doyle Spirals." (Feb 2, 2017) www.josleys.com/articles/HexCirclePackings.pdf.
      [3] A. Sutcliffe, "Doyle Spiral Circle Packings Animated." (Feb 2, 2017) archive.bridgesmathart.org/2008/bridges2008-131.html.

License Information