Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a Dorogovtsev–Goltsev–Mendes graph
ResourceFunction["DorogovtsevGoltsevMendesGraph"][n] gives the Dorogovtsev-Goltsev-Mendes graph of order n. |
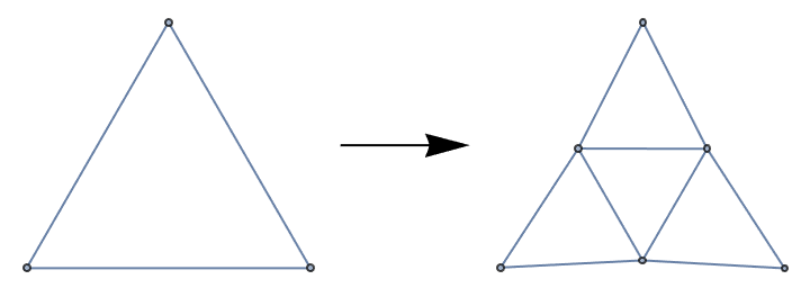
A Dorogovtsev-Goltsev-Mendes graph of order 3:
| In[1]:= |
| Out[1]= | 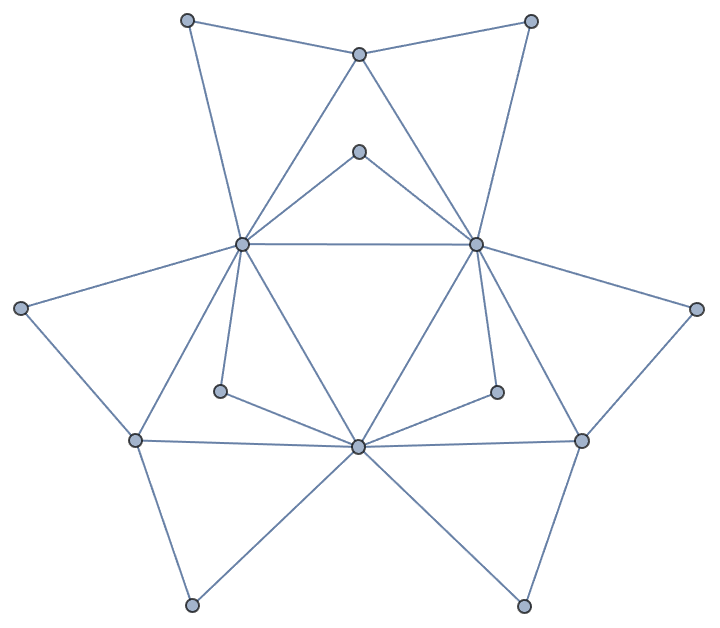 |
Dorogovtsev-Goltsev-Mendes graphs quickly become very complex:
| In[2]:= |
| Out[2]= | 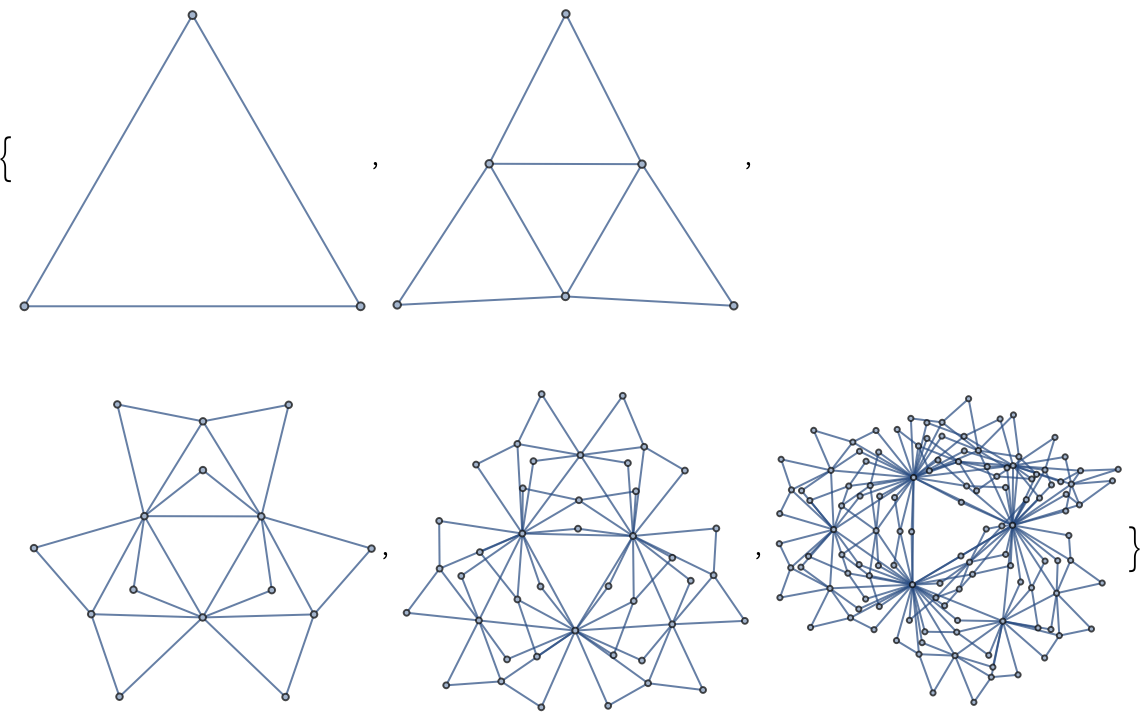 |
The number of edges grows exponentially:
| In[3]:= |
| Out[3]= |
Show a 3D embedding of a Dorogovtsev-Goltsev-Mendes graph:
| In[4]:= |
| Out[4]= | 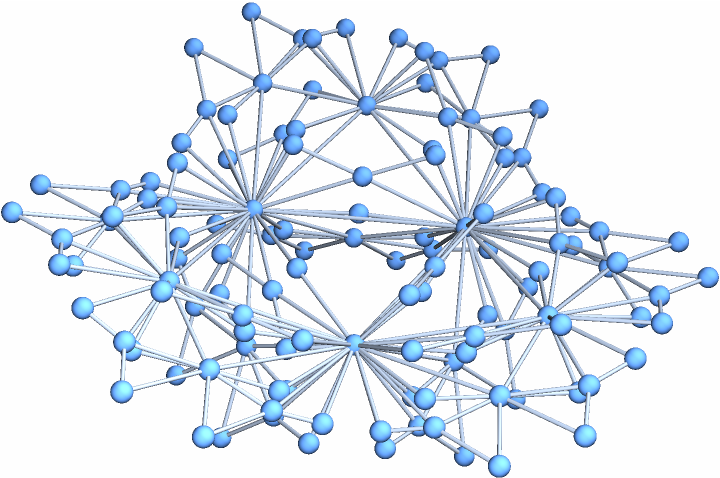 |
Visualize the adjacency matrix of a Dorogovtsev-Goltsev-Mendes graph:
| In[5]:= |
| Out[5]= |  |
DorogovtsevGoltsevMendesGraph[0] is equivalent to a path graph with two vertices:
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |
DorogovtsevGoltsevMendesGraph[1] is equivalent to a cycle graph with three vertices:
| In[8]:= |
| Out[8]= | 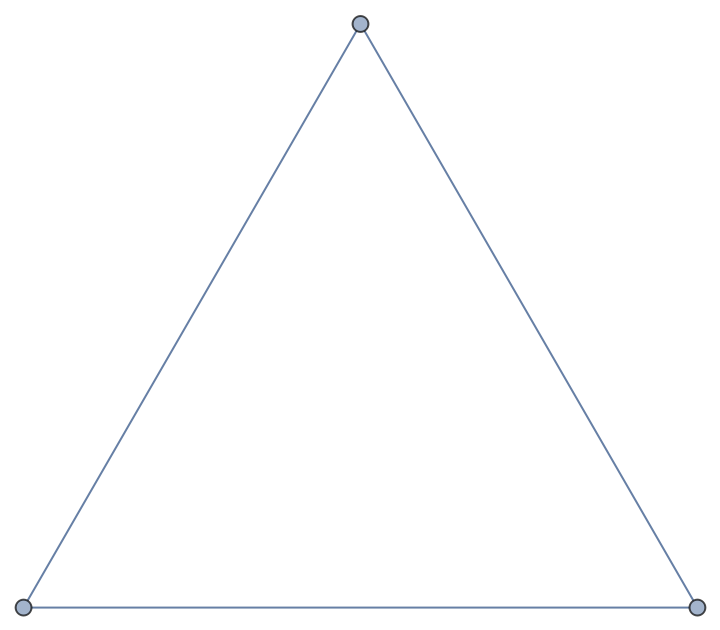 |
| In[9]:= |
| Out[9]= |
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License