Basic Examples (1)
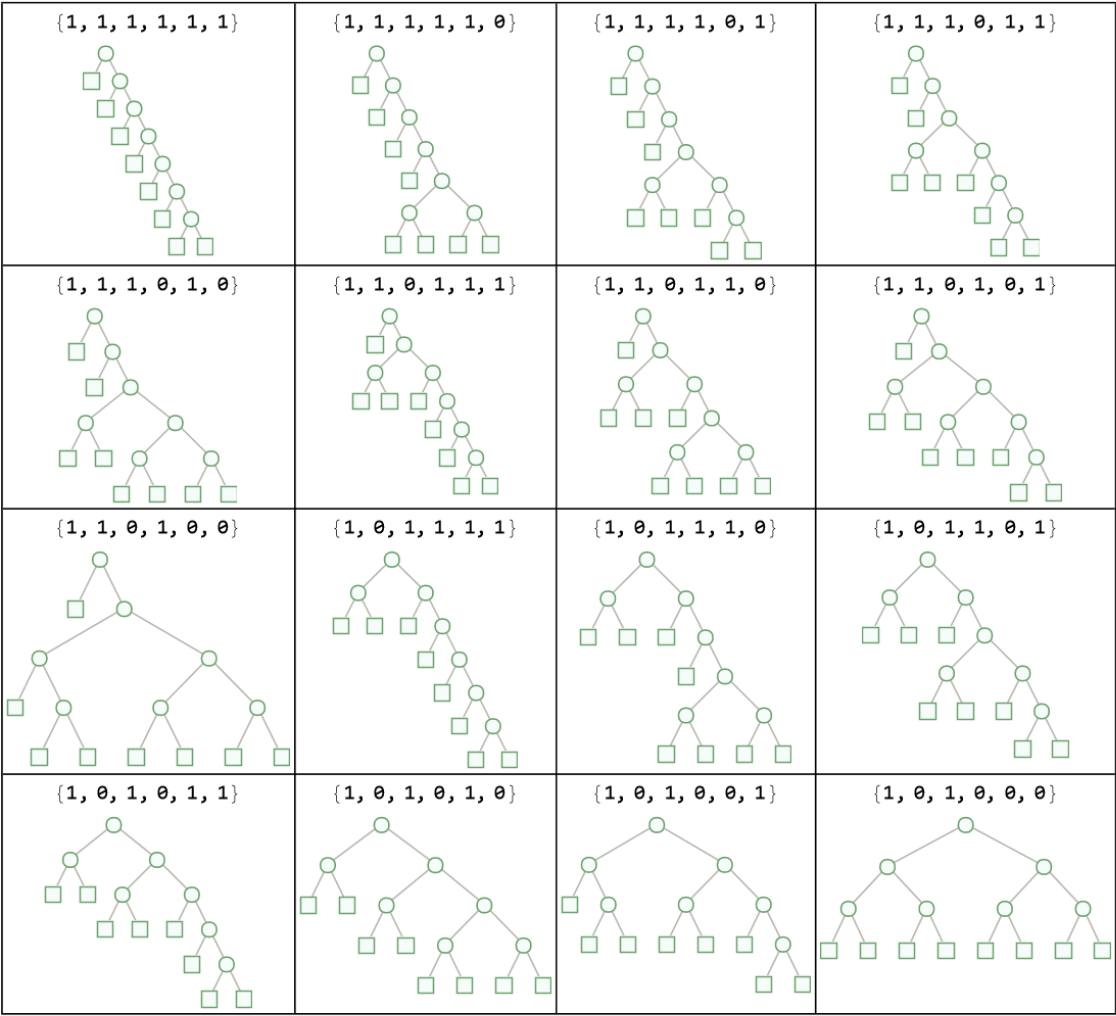
Enumerate all 16 proper six-bit binary codes corresponding to non-equivalent compact Huffman trees with 8 leaves in a "BitVector" data structure:
Scope (3)
List all 16 six-bit binary codes that satisfy the proper conditions given enumeration data in bit vector:
Find the compact Huffman tree for the proper 8-bit code {1, 1, 0, 1, 0, 0, 0, 1}:
Demonstrate the process for constructing the tree corresponding to the code {1, 1, 0, 1, 0, 0, 0, 1} as described in Details & Options above:
Applications (1)
DistinctCompactBinaryHuffmanCode provides a way to generate random trees with certain constraints. For instance, for n=22, instead of generating all 175586 24-leaf distinct compact Huffman trees at once, we randomly generate an index first and access the corresponding binary code from the bit vector:
Properties and Relations (3)
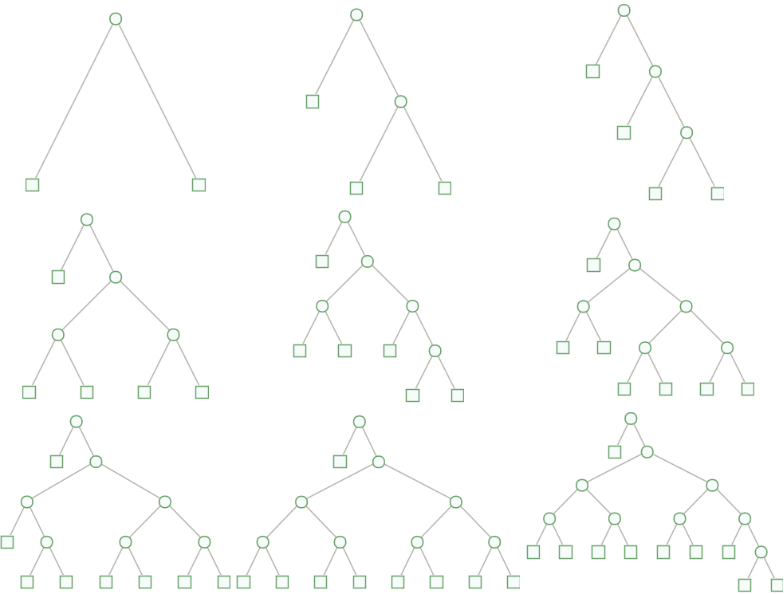
There is one-to-one correspondence between proper n-bit binary codes and (n+2)-leaf non-equivalent compact Huffman trees. For example when n=6:
All trees above have 8=6+2 leaves:
All trees above have one depth greater than the number of ones in the binary code:
Possible Issues (4)
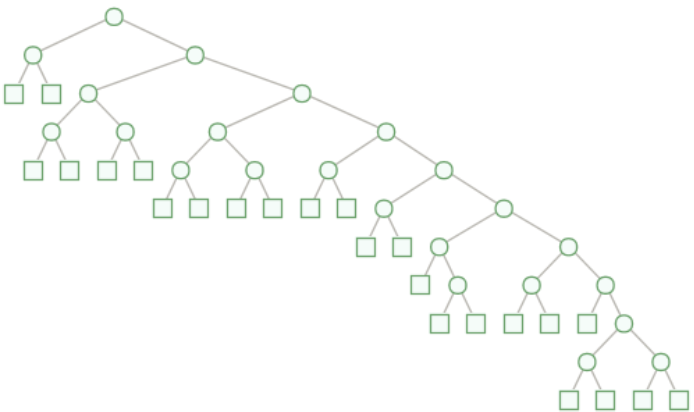
The number of n-bit proper codes and the corresponding trees grow rapidly with bit length n. For instance a 60-bit code has more than 7.7 trillion candidates. Therefore use "CountOnly" to bypass the enumeration function and avoid binary code generation:
DistinctCompactBinaryHuffmanCode returns unevaluated for large bit-code length:
Only binary code is supported:
The following example does not meet the proper conditions described above in Details & Options. Reading from left to right, we have a run of one zero and a next run of 6 zeros. Since 6 > 2·1+1, this binary code fails to correspond to a compact Huffman tree:
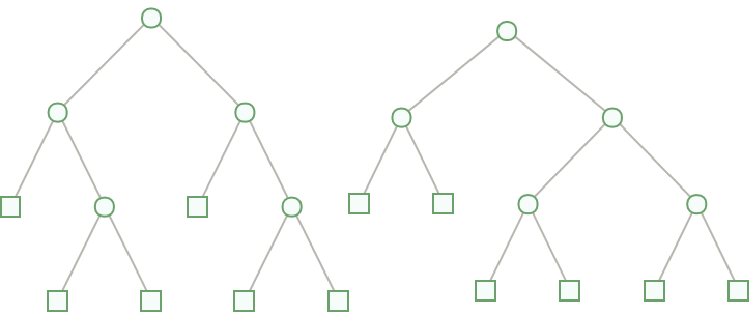
The concept of equivalence for compact Huffman trees is not the same as graph isomorphism. The following two trees are considered equivalent Huffman trees (Even and Lempel, 1972), but obviously they are not isomorphic in graph-theoretical sense:
Neat Examples (2)
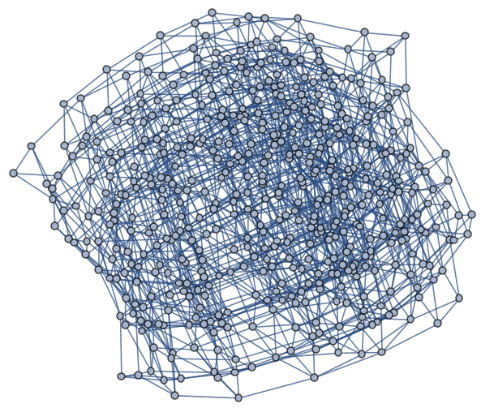
Plot a large graph from the 12-dimensional proper codes. Points are connected if their Hamming distances meet a predefined value:
If the target Hamming distance is 1:
If the target Hamming distance is 2:
Visualize the compact codes with ArrayPlot:

![assoProperCode = ResourceFunction["DistinctCompactBinaryHuffmanCode"][6];
With[{
bv = assoProperCode["TreeEnumerationBitVector"],
tc = assoProperCode["TreeCount"],
bcl = assoProperCode["BitCodeLength"]},
Table[bv["BitGet", i + bcl*j], {j, 0, tc - 1}, {i, 0, bcl - 1}]
] // Grid](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d59c033-4813-4df4-8f9a-8c97612b83bd/23f6051bf19b9cc8.png)

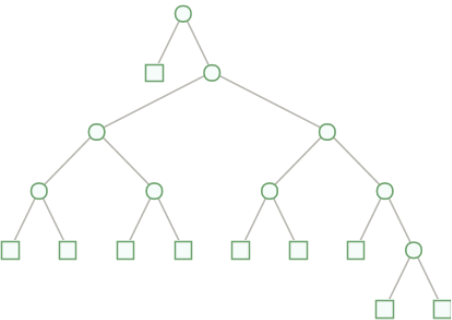
![Grid[ResourceFunction[
"DistinctCompactBinaryHuffmanCode"][{1, 1, 0, 1, 0, 0, 0, 1}, "TreeFormWithSteps"] // Partition[#, UpTo[3]] &]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d59c033-4813-4df4-8f9a-8c97612b83bd/4b853a7c940ab318.png)

![SeedRandom["Huffman"];
indx = RandomInteger[175586] - 1;
Array[bv["BitGet", #] &, 22, 22*indx]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d59c033-4813-4df4-8f9a-8c97612b83bd/6258f935927ef644.png)
![assoProperCode = ResourceFunction["DistinctCompactBinaryHuffmanCode"][6];
codes = With[{
bv = assoProperCode["TreeEnumerationBitVector"],
tc = assoProperCode["TreeCount"],
bcl = assoProperCode["BitCodeLength"]},
Table[bv["BitGet", i + bcl*j], {j, 0, tc - 1}, {i, 0, bcl - 1}]
];
trees = ResourceFunction["DistinctCompactBinaryHuffmanCode"][#, "TreeForm"] & /@ codes;
With[{res = MapThread[Labeled[#1, #2] &, {codes, trees}]},
Grid[res // Partition[#, UpTo[4]] &, Dividers -> All]]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d59c033-4813-4df4-8f9a-8c97612b83bd/27340b6161e08993.png)
![pair = {Tree[
1, {Tree[1, {0, Tree[1, {0, 0}]}], Tree[1, {0, Tree[1, {0, 0}]}]},
TreeElementLabel -> All -> None],
Tree[1, {Tree[1, {0, 0}], Tree[1, {Tree[1, {0, 0}], Tree[1, {0, 0}]}]}, TreeElementLabel -> All -> None]};
pair // Row](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d59c033-4813-4df4-8f9a-8c97612b83bd/0a3926ab82d3afbe.png)
![assoProperCode = ResourceFunction["DistinctCompactBinaryHuffmanCode"][12];
codes = With[{
bv = assoProperCode["TreeEnumerationBitVector"],
tc = assoProperCode["TreeCount"],
bcl = assoProperCode["BitCodeLength"]},
Table[bv["BitGet", i + bcl*j], {j, 0, tc - 1}, {i, 0, bcl - 1}]
];](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d59c033-4813-4df4-8f9a-8c97612b83bd/0eaccc61f1ab2ada.png)
![Graph[
UndirectedEdge @@@ Cases[edges, _?(HammingDistance @@ # == 1 &)],
GraphLayout -> "SpringElectricalEmbedding"]](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d59c033-4813-4df4-8f9a-8c97612b83bd/709d55c376c08825.png)

![assoProperCode = ResourceFunction["DistinctCompactBinaryHuffmanCode"][9];
codes = With[{
bv = assoProperCode["TreeEnumerationBitVector"],
tc = assoProperCode["TreeCount"],
bcl = assoProperCode["BitCodeLength"]},
Table[bv["BitGet", i + bcl*j], {j, 0, tc - 1}, {i, 0, bcl - 1}]
];](https://www.wolframcloud.com/obj/resourcesystem/images/8d5/8d59c033-4813-4df4-8f9a-8c97612b83bd/7fed6e18656de341.png)
