Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Render a graph with vertices at heights based on their distance from the root
ResourceFunction["DistanceLayeredGraph"][g] renders the graph g so that nodes that are a distance d from node 1 are at position d below the root. | |
ResourceFunction["DistanceLayeredGraph"][g,root] uses the specified node root as the root. |
Organize nodes in a graph based on distance from node 1:
| In[1]:= | ![ResourceFunction["DistanceLayeredGraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7}, {{{1, 2}, {1, 2}, {1, 2}, {1, 3}, {1, 3}, {2, 4}, {2, 4}, {2, 3}, {2, 5}, {2, 5}, {3, 4}, {3, 6}, {3, 5}, {3, 7}, {
3, 7}, {4, 6}, {4, 6}, {5, 7}}, Null}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJxtlgs4VOkfx2fcZtyG3Nqykm6UtGqpZTe/d4tQKlFJV9luSyWxUnJNCmtV
aovE312XLVRbLvUi1wqhoqQVch1jZhh35s90zvTsefZ95nnm+c5555z3837m
fOfoOLvZ7Zeg0WjL6TTa1Pu/hzL6d2YSmQvEB2TGlM9p/87kcfFA/z1PfH78
3/PE14N/v3/9XLlsu65KTyKUB78qvK+rhNCJnNK6vWnwyuKY2x9cFkJ/ze2O
1b8N7IHvFOMes5BTUKnzXKu7sK6tNUcygIXKjELKy7dnQOAmibGmNSy07cK+
YjOTTPh4syDZQZGFMrZHcthPM+GitGZJaK0i4m56POtsdyZEi8bXfPDA1JAT
z3cbaTXxWiwnPt/crWY70vmy4uv53x2X1M6WRbbEev6eoWkx5i+LDIn1qsu+
4u+1nMwEj2FO5AV3JVlEI3hX+Hy30qaeiQh+TOHHFH5M4ccUfkzhxxR+TOHH
FH5M4ccUfkzhxxR+TOHHFH5M4cckv75JV2WEUha0Htn+RvuZEnrbsvygVVEh
aGTs6Lh/TAk922LhH2xcAVdKJE3ymEposcmrq08MXsOuTLvSH8JZqPLbeT9p
aL6H48esohYOKaLmRRs1DixtgteSn2P/2KiImMfjH7gFtUCgq17rwYsK6F2L
xHAarR1Opan8+vCJPNoScLKFdacL8KMk/ROv5VCy44K5OjfZ4NHag55byaHP
oZEqJq4cMDXeFTb6tyzSmPYwcyu/F9Ru8Rjy2rIo5sQ62sp4LghX3c4eCmCi
2Zdi/Kt1eTAmDI0v+sBAs+pL33Zc4oHCp4jso8sY6LJ1rfSZJh4safubMRgo
gwLb8hT+p8wHZyXpsF0vpNHnu8HdMJcP6Tu9USJLGv14d4M5T5sPxiofBQs3
S6GxXrPsVSw+gKfkb47Jkmih55a1RhweFAV1PDEUSqB800uDxXgyr4x4dW+f
BHq2WpA/GMQDsxTenbev6WhZpF9q+QoeLM9Wt0/ZSEfyWkvSf/zIhfSTw4Wa
b2jItkeyZL0XF/5six0z2U9D7Mi8B/4vY+Ca0qOYF15KKOhmZ8f1iXuQuHNr
tHILC9mpVKuHteaCZnvjaKU5CzlwEvRclhaD5L31hTKxiogdfcBe40kF7HyQ
wn7UoYD4FteLk5/XwoLBz6eaFykgnWZmB33XO9hzgnUkxFkendEZu5B45R+Q
M9Z+lhQphxSCTJ1Wm7bAPMNvfE2zZJGL9VWzTNnPcGa21Gm/5bKIn2pBy0ho
A59bYUoKD5koOcYiBSQ6QLHy9ooWAybyn3fVwEm/E5aHH+yXTGCgYHPT6Gla
XTDw6YnFURYDZY0s6bCv6wK7mrv6c7xkkJzlbzN1t3eD+U7TVO16afT7QkXD
8JRuqPR3enjASBotTxzQC8juBt5POo6DYVIoLMn5hFZ+N0SXtAt+a5FEzNlB
EadauuHhRm1uiIUkypq+xfXqXDaY15daLsqUQIFhDcqeAZPZ6dPYngUSyMdb
3U95hA2P2l2V9FLoKO6TxP3DF3og7uhB/yADOuoqTrp3fjUHBvprbdwwDe2d
P+SxT7UXCk9lnuBsF/vBX/wwSD84QeRHhvSDZ4r8yJB+8Bc/0qQf/MWPFOkH
f/EjRfrBTiI/kqQfLC/yI0H6wfNFfuikHxws8kMn/WBfkR8a6QezRH5opB98
WKOqg7FKCIQf3PvMJ/zDtxNA+MGJybsczNljQPjBIY89bSBjFAg/OFaY71Jx
aAQIP7j55KosjvowEH7w9xFV3d0lg0D4wb/GmzUphg8A4Qefy4iM3OwsAMIP
Pp9fOIxt+oHwg49W1c2yXdsHhB9s2lg5IbWDD4QfzO5Mi/7oxwPCDw4WOPd+
eMgFot/wZ1G/Mch+w9NF/cYg+w1fFvUbg+w3/KXfZMh+wx6ifpMm+w1/6Tdp
st9wkKjfpMh+wz6ifpMk+w3ni/pNguw37CnqNwmy3/CPon6jk/2G1UX9Rif7
DdNWT/Ubjew3PCpUhdBsIRD9hmcWano07psAot/w7pdHlDiS40D0Gy6ZJaeW
++coEP2G7bK5AeZaI0D0Gz48L6/bPn0IiH7Dvh0yXVlWg0D0Gz4nXe2zd0IA
RL/hEJ+ZCXvK+4HoN3x6bYvjXzf7gOg37HJcP3VtPB+IfsO2ffyzK27xgOg3
bFBhMuzxnAtrsDAzQCMONlfVF3fHMxDjAVfZZdMdyLKa4Z1jzEBXzDqjzDrv
w/TDBRqHC2RQyI2ayp9KH0OISXUCbbUMqvMyyr5XmAfjGVNfkEbnn7PsrzZg
8KvR9a3RlUY2Lw0rh5kFwIw7WqEULoWCj/25tjmrAKJVteQMWyURW/T/WwBG
308NSdRN5NdTX/eVEB93/7Z08kVHPURWmTY16OLjmdI7MqR30MT5f/3W8f3W
QiDzx8apMS7OWlOncx8T550ZUycYFecY0fPBMJwh1ivanhVDQPL0PZuzv6lz
AEIJXsbU5TMEQO4HQ8TbD+R+CX7flTdxsg/I/RRtjy8fZIj9Fk2/zIN1hI9t
ezd46uWL/WCKH0zxgyl+MMUPpvjBFD+Y4gdT/GCKH0zxgyl+MMUPpvjBFD+Y
4gdT/GCKH0zxgyl+MMUPpvjBFD+Y4gdT/GCKH0z6IZ/j0+Iyw+tAKM7OF5dx
PV0ngE7kJfVBBvVB4+LjCh6Jq+khY+I8snfqC6Nfc/LGqdfX+T81xmhrDIvz
Ul1TNaeyQXEWPb4eGIDFbUWy1Q29oGUcy/KTFsD9a6q65m69UFapHsbP6YNL
09kOjjkcOPR9bf2zED6UOm+IVX7SA4POr0d4h3jgcMq0/9cTbPDZNYN7ei8X
0O6MPfs7u+CThbl7eRMHglgZHyVUO+HBgcZ0O/0emBVu4r6qvw1ctSZCriR2
g/Jrm+nzIlqB6ZIqf2lNF9hkDyfUzKgHu6N+6Z4ybcCUHK1e+CEf9jqB6VnN
ZmCPufKeJT3C+wJqAs/JN0J/mRILumtwiOaQt1PYW0hsmG3z5tpH/N2lXscr
919BkqZlwzvvVpxT5m5twyoFfs/tBT0jHdjEynb/OrU8yG01O59cw8b675lP
G1xuQlQS58PQbB48b3hwC0KEcPpDm0LoNj4YOD16dfDTBGTf6ojMSO0DvQjG
ce9pE2DD6t/vJi+AHOeUP9w1xsGIIRtZHDIArU0XFthzR+H4FV35+98MQRrj
uYlW/AjIZG98v6Jg0kudbVnVnGHguAeO2QeMQv+G+TUuPoOwOD/PnbF1HPzc
LB046QKoXRx18cLmCWgvawi8fLEfBEWWobHGQvjNJUdt8Egf/H7+/Tb9YSHo
bW5R0jDjQ0Xu/IC4jTQ0cXarB4/OA2XrCtwRRUN9Ql0/FY9eUGL/4upZTkPL
gle05ZSzoTy5M+hnLg09vtYw6wOjC5DHbhlbJh2FrVTT8zJoh+MOhYL4yfsy
8fgneqhpK2g56CYOKdHRWyvvujTbTzBxIn6nDmPyuSVBM/3FnEZQz1k0f+Yg
DWlomPeeHa4DJ63y0eZ/aEiN82uw3/xaaE441eRTQENN9jOrXNZXQLQl1LZe
pyG7qB1Lt4wUQQhr+mstNxoaNvpuj3dSDqQP0FsW/EhDYSkmuv4bbgLwayaW
unLBUPuo8dWeyf1fb/lPv5ALq7LvLNMpGYcF03YlWD3lgVFl7uCN0DF4sVLN
wiB18r7cfT1Y8YdRMKs9/DzxUR88PrTunVv1MJyuPrD0Jr8fbDgvBEVbhuD8
DxKnkMMA5HO+fa9QPABOTEg+9HkQ1F3MQiy1BSDzs1aGzo1hsHYyHPHc1wcP
ktfF1wePAPNn5tDYYT6crJ1Dq7cdheHN6trfuPBgc0VijTZ9DDRjHdxKdkze
H5deaGRcGYO6xXHVSsEcWDXnxsvzrHFoPDeokW3CBkff6f03XcfBwjr37vn6
TjibZBqh+tc4KLh3XvNzaoeSyzLXimvG4Qdh4JuY6lbQ3OSjlv9hHIr6gvc1
6jdD0abMXFbTOLw0Mrt3T/MfkFIuWPOENw5pviMBKxa/h/rwWw9fTP5uZxSa
mdmFvgFUfIRpiiZAS0K+XbisGlbmyQHTdwLcfZ4OBNg9h6pjgY7LyybgTafX
gG59IQiaqx2KdIRQFOcX09nzCDJUxkyyQoVwLGM3+0ZuKvjbhzUuqebguaqr
5Kvi2PD7tuAzzaEcDNMLnpgUdsPi4vVL16zn4L8asJF3cxe8P1db7qvJwYui
o7pZtC44aFJVktrfg6XWyHLPaHaC4Ii9bn19D/ZKk4nabdwBt9SWOM8p68Hm
Goe/0d3QDoUCvZ2RhT14n6jP2sRZ9Pfzfa14vketblXmL9Xi8+k4f75/dlGV
+Hod7e+Be/EFNBDrsb2eualIWAoGxHrNL9IMtL2KIILgmUgcZc4YzIcAgvft
gd6Uc7K5gN6aXjx0lSvmz6ld+ZSVyxXzu2g5tu98xxXzq04+rf7M54r5bX65
FntHmifml7Heyo5S5Yn5bws6KjmaPDG/9tmpf1iemJ/MJD85n+Qnz0fyk9cj
+VWI9ZD85HpJfpKH5Cd5Sf7/Ax3tR7Q=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[
BezierCurveBox[{1, {0.16444074718311652`, 3.4999999999999987`}, 2}], 0.03700564971751412], ArrowBox[{1, 2}, 0.03700564971751412], ArrowBox[
BezierCurveBox[{1, {-0.16444074718311652`, 3.4999999999999987`}, 2}], 0.03700564971751412], ArrowBox[BezierCurveBox[{1, 45, 46, 47, 48, 49, 50, 51, 52,
53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 3}], 0.03700564971751412], ArrowBox[BezierCurveBox[{1, 71, 72, 73, 74, 75, 76, 77, 78,
79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 3}], 0.03700564971751412], ArrowBox[{2, 3}, 0.03700564971751412], ArrowBox[BezierCurveBox[{2, 97, 98, 99, 100, 101, 102, 103,
104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 4}], 0.03700564971751412], ArrowBox[BezierCurveBox[{2, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 4}], 0.03700564971751412], ArrowBox[BezierCurveBox[{2, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 5}], 0.03700564971751412], ArrowBox[BezierCurveBox[{2, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 5}], 0.03700564971751412], ArrowBox[{3, 4}, 0.03700564971751412], ArrowBox[{3, 5}, 0.03700564971751412], ArrowBox[BezierCurveBox[{3, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 6}], 0.03700564971751412], ArrowBox[BezierCurveBox[{3, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 7}], 0.03700564971751412], ArrowBox[BezierCurveBox[{3, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 7}], 0.03700564971751412], ArrowBox[
BezierCurveBox[{4, {-0.8355592528168823, 0.5000000000000041}, 6}], 0.03700564971751412], ArrowBox[
BezierCurveBox[{4, {-1.1644407471831195`, 0.5000000000000049}, 6}], 0.03700564971751412], ArrowBox[{5, 7}, 0.03700564971751412]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.03700564971751412], DiskBox[2, 0.03700564971751412], DiskBox[3, 0.03700564971751412], DiskBox[4, 0.03700564971751412], DiskBox[5, 0.03700564971751412], DiskBox[6, 0.03700564971751412], DiskBox[7, 0.03700564971751412]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
ExpressionUUID -> "52e5d8ec-d65d-410f-bf93-3a4da6e5599a",
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{134.6171614141531, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/2cf/2cf1b568-f672-456d-a03c-3d11bc044a25/4748b17b502bec7a.png) |
| Out[1]= | 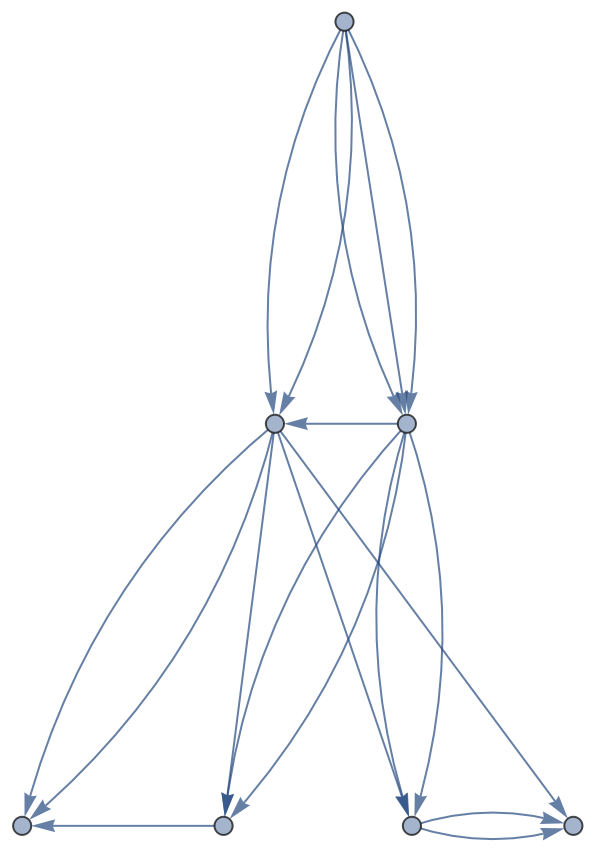 |
Create a layered rendering of a 2D grid graph:
| In[2]:= |
| Out[2]= |  |
In a complete graph, all nodes are distance one from node 1:
| In[3]:= |
| Out[3]= | 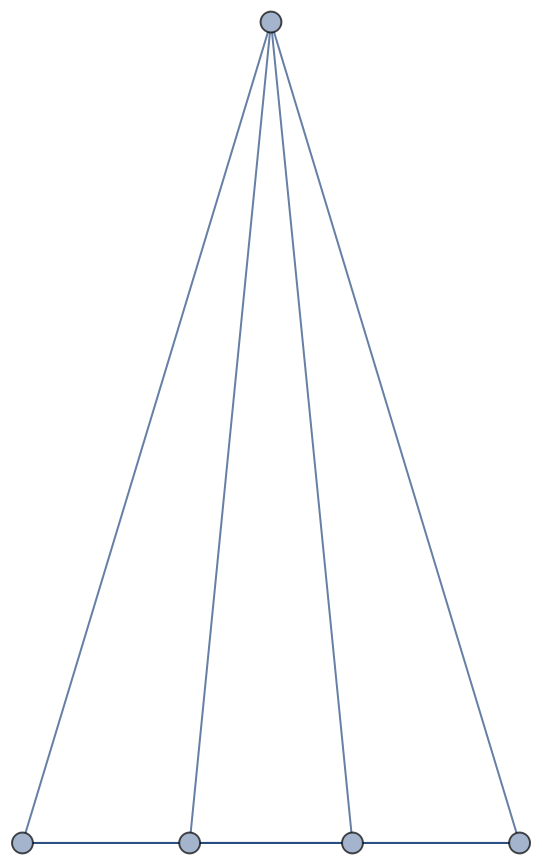 |
This work is licensed under a Creative Commons Attribution 4.0 International License