Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get uniformly distributed points on a disk
ResourceFunction["DiskPoints"][n] gives the positions of n uniformly distributed points on a unit disk. |
500 uniformly distributed points on a unit disk:
| In[1]:= |
| Out[1]= |  |
Compare this with the boundaries of a unit disk:
| In[2]:= |
| Out[2]= | 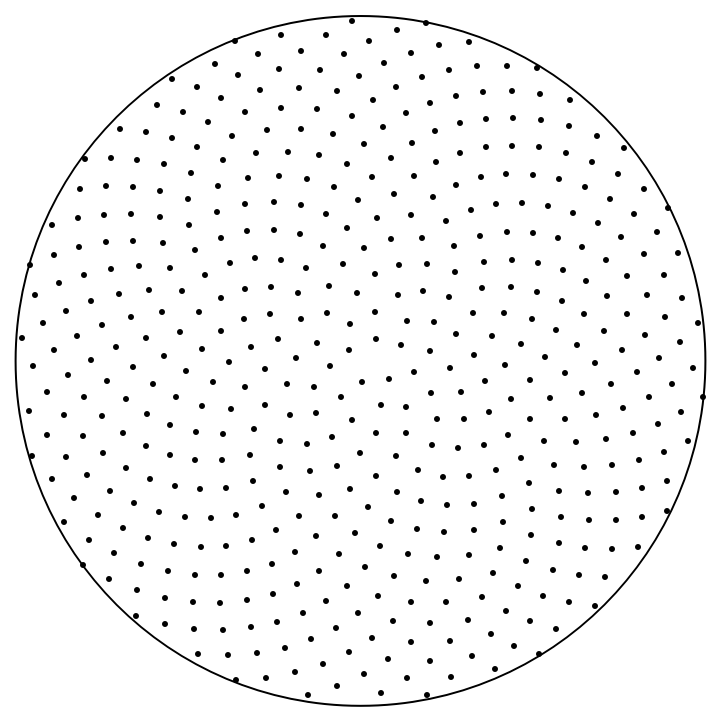 |
Use DiskPoints to make a uniform mesh:
| In[3]:= |
| Out[3]= | 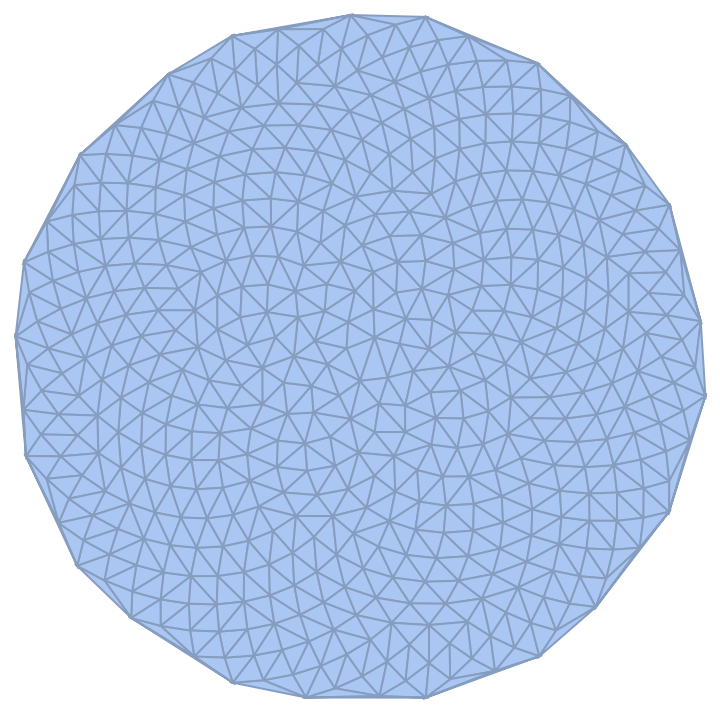 |
Connect each point to its nearest neighbor:
| In[4]:= | ![pts = ResourceFunction["DiskPoints"][1200];
nf = Nearest[pts];
pairs = {#, nf[#, {2, \[Infinity]}][[-1]]} & /@ pts;
Graphics[{Circle[], Line@pairs, Point[pts]}]](https://www.wolframcloud.com/obj/resourcesystem/images/71e/71e3323a-848a-465b-9a72-089663f0ecdd/7b5cdac24da64944.png) |
| Out[5]= |  |
Highlight the non-uniformity in the area determined using Voronoi analysis:
| In[6]:= | ![pts = ResourceFunction["DiskPoints"][1000];
pols = MeshPrimitives[VoronoiMesh[pts], 2];
val = Median[Area /@ pols] 1.4;
pols = Select[pols, Area/*LessThan[val]];
areas = Rescale[Area /@ pols];
Graphics[{ColorData["Rainbow"] /@ areas, pols} // Transpose]](https://www.wolframcloud.com/obj/resourcesystem/images/71e/71e3323a-848a-465b-9a72-089663f0ecdd/6f9d2e113fde7cc3.png) |
| Out[7]= | 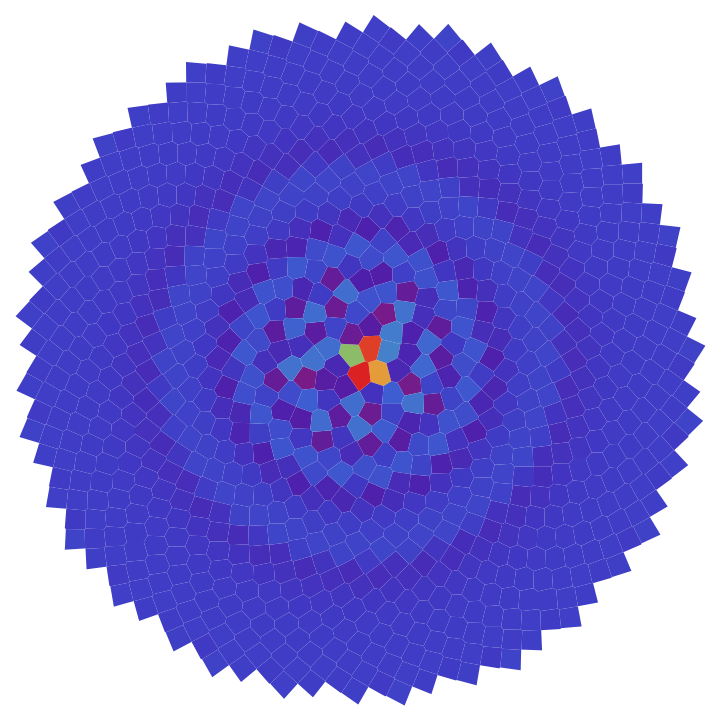 |
Find the minimum spanning tree for 2000 points, and show the connectedness:
| In[8]:= |
| Out[8]= | 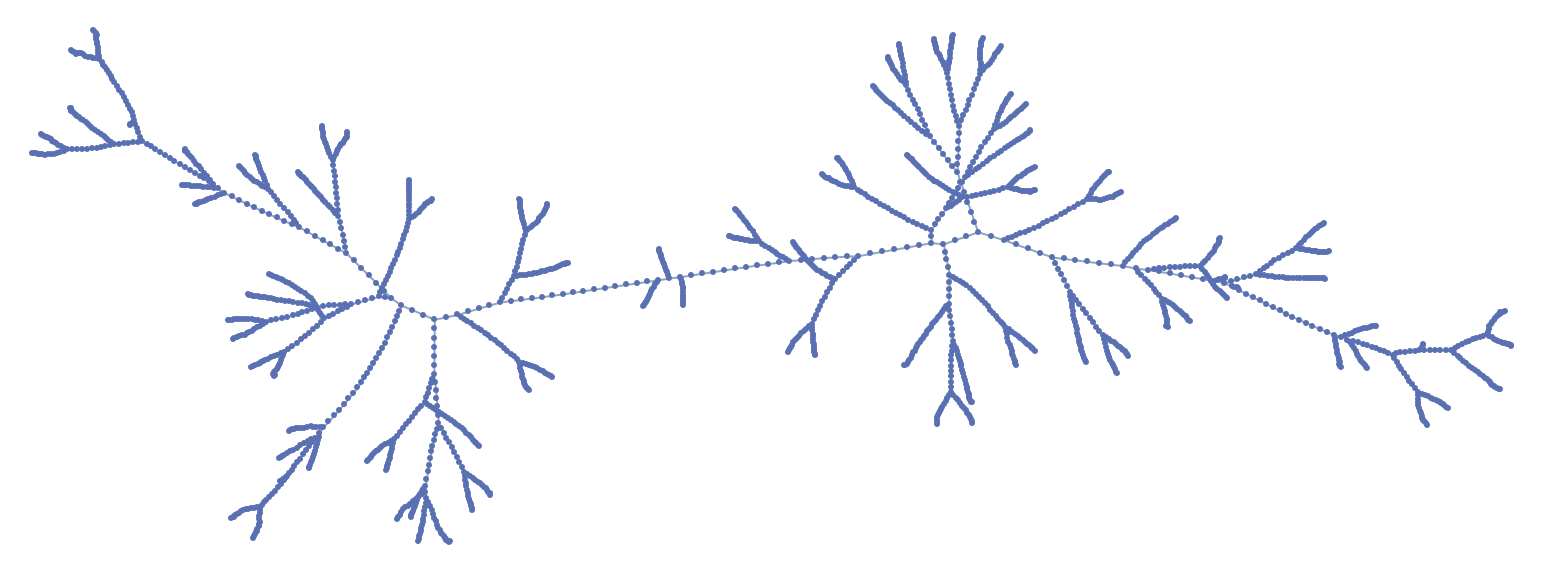 |
This work is licensed under a Creative Commons Attribution 4.0 International License