Function Repository Resource:

DiscreteIntegralPlot

Plot and find the area of a region determined by a list of points, the x axis and the type of boundary

Contributed by: Dennis M Schneider

ResourceFunction["DiscreteIntegralPlot"][data,method]

plots the region determined by data, the x-axis and the type of boundary and prints the area of that the region.

Details and Options

"DrawGraph" is an option for ResourceFunction["DiscreteIntegralPlot"] which, if set to False, will suppress the graph and just return the area of the region.

"PrintDisplay" is an option for ResourceFunction["DiscreteIntegralPlot"] which, if set to False, will suppress the printing of the area of the region.

Other options are those for Plot, ListPlot, ListLinePlot or Graphics.

The method can be specified as Left, Midpoint, Right, Upper, Lower, Trap, Simpson or Spline.

Examples

Basic Examples (1)

Plot data and determine the area of the region determined by data and the x-axis, using the left–hand endpoints as the height of the rectangles:

In[1]:=

data = {{0, 0.8121}, {1, 1.3904}, {2, 2.8374}, {3, 3.1539}, {4, 4.134}, {5, 5.3356}, {6, 6.7651}, {7, 7.6077}, {8., 8.9556}, {9, 9.3877}, {10, 10.8627}, {11, 11.8943}, {12, 12.8101}, {13, 13.6069}, {14, 14.4239}, {15, 15.1200}, {16, 16.3355},
{17, 17.0501}, {18, 18.7869}, {19, 19.2568}, {20, 20.5573}, {21, 21.0866}, {22, 22.7888}, {23, 23.3589}, {24, 24.7452}, {25, 25.6962}, {26, 26.9515}, {27, 27.2051}, {28, 28.6112}, {29, 29.3606}, {30, 30.1864}, {31, 31.5974}, {32, 32.6556}, {33, 33.9730}, {34, 34.3237}, {35, 35.4104}, {36, 36.8455}, {37, 37.3661}, {38, 38.8999}, {39, 39.2904}, {40, 40.5100}};
ResourceFunction["DiscreteIntegralPlot"][data, Left]

Out[2]=

Scope (6)

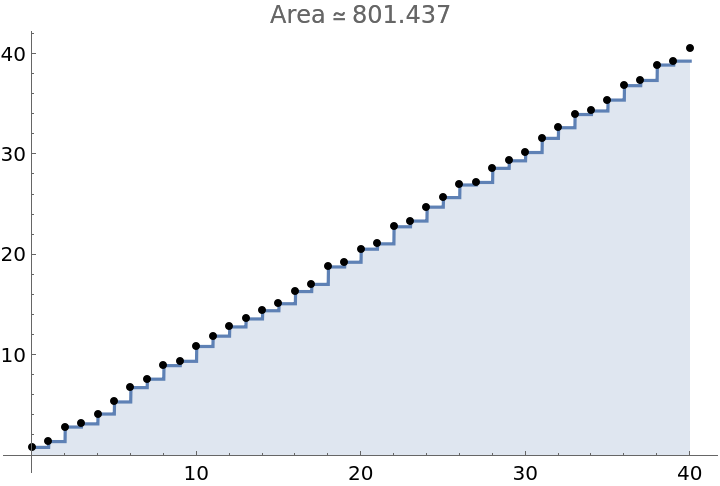Use data given by a formula:

In[3]:=

$data1 = Table[{x, Sin[x^2]}, {x, 0, 4, .1}]; ResourceFunction["DiscreteIntegralPlot"][data1, Right, ImageSize -> 300]$

Out[4]=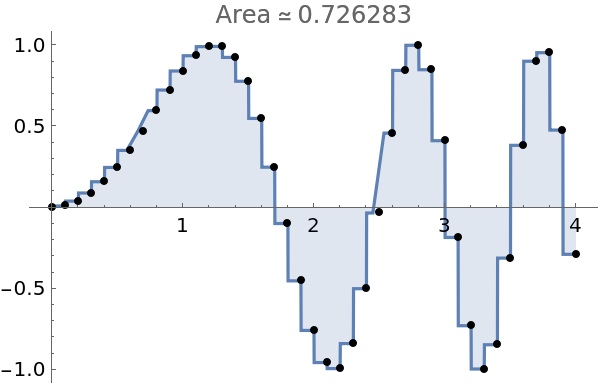

Note the bad spots in this graph around x=0.6 and x=2.5. Plotting more points fixes the problem:

In[5]:=

$data1 = Table[{x, Sin[x^2]}, {x, 0, 4, .1}]; ResourceFunction["DiscreteIntegralPlot"][data1, Right, PlotPoints -> 60, ImageSize -> 300]$

Out[6]=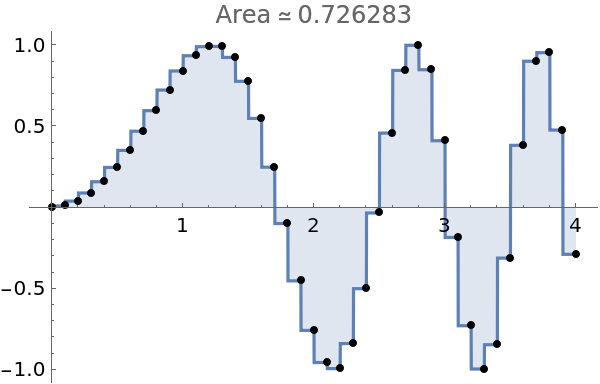

Apply a style to the region:

In[7]:=

$data1 = Table[{x, Sin[x^2]}, {x, 0, 4, .1}]; ResourceFunction["DiscreteIntegralPlot"][data1, Midpoint, FillingStyle -> {Red, Yellow}, ImageSize -> 300]$

Out[8]=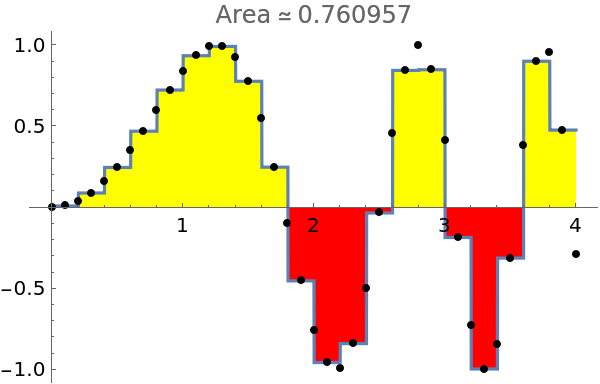

Apply a style to the points:

In[9]:=

$data1 = Table[{x, Sin[x^2]}, {x, 0, 4, .1}]; ResourceFunction["DiscreteIntegralPlot"][data1, Simpson, FillingStyle -> {Red, Yellow}, "PointStyle" -> {{PointSize[.02], Blue}}, ImageSize -> 300]$

Out[10]=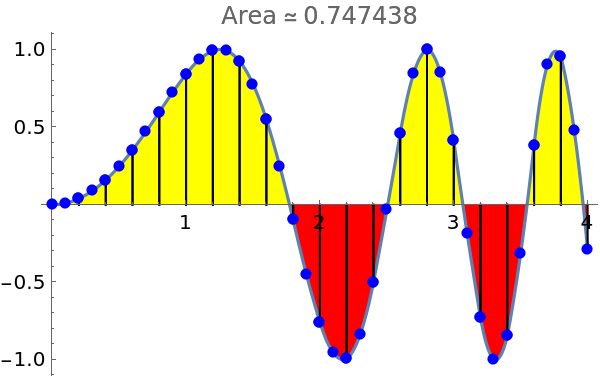

Use Manipulate to illustrate all possible methods to be used:

In[11]:=

$data1 = Table[{x, Sin[x^2]}, {x, 0, 4, .1}]; Manipulate[ ResourceFunction["DiscreteIntegralPlot"][data1, method, PlotPoints -> 60, FillingStyle -> {Red, Yellow}, ImageSize -> 300], {method, {Left, Midpoint, Right, Upper, Lower, Trap, Simpson, Spline}}]$

Out[12]=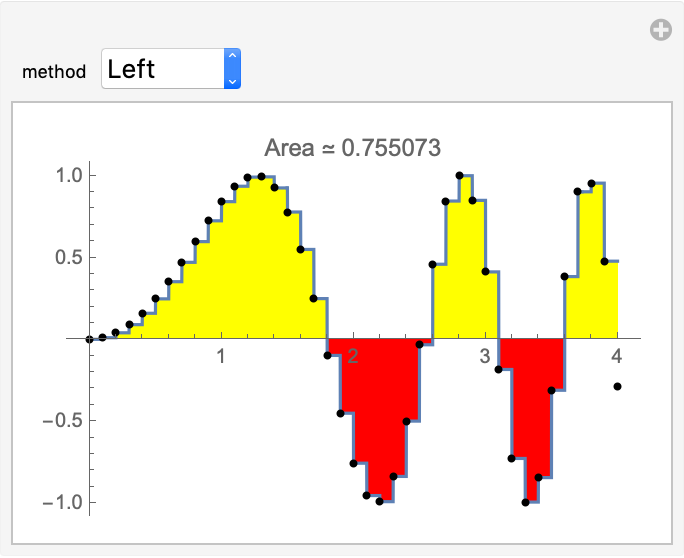

Setting the option "DrawGraph" to False suppresses the plot of the region and returns the area:

In[13]:=

$data1 = Table[{x, Sin[x^2]}, {x, 0, 4, .1}]; ResourceFunction["DiscreteIntegralPlot"][data1, Simpson, "DrawGraph" -> False]$

Out[14]=

Possible Issues (2)

Data must be ordered:

In[15]:=

Simpson's method requires an even number of subintervals and the range should be chosen accordingly:

In[16]:=

$data1 = Table[{x, Sin[x^2]}, {x, 0, 4.1, .1}]; ResourceFunction["DiscreteIntegralPlot"][data1, Simpson, PlotPoints -> 60, FillingStyle -> {Red, Yellow}, ImageSize -> 300]$