Function Repository Resource:

DirectionalDerivative

Compute the directional derivative of a function at a point

Contributed by: Dennis M Schneider

ResourceFunction["DirectionalDerivative"][f,vars,pt,v]

computes the directional derivative of the function f of the variables vars at the point pt in the direction of the normalized vector v.

Details and Options

When the function is differentiable at a point (a₁,a₂,…), then the directional derivative at (a₁,a₂,…) in a direction

can be calculated using the formula

where

is a unit vector.

The formula

for the directional derivative at a point (a₁,a₂,…) requires that the function be differentiable at the point (a₁,a₂,…). Setting the option "UseLimit" to true allows the computation of the directional derivative for non-differentiable functions.

If the formula is applied to a function whose gradient at a point is 0, then it will return 0 independent of the specified direction.

Examples

Basic Examples (2)

The directional derivative of a function of two variables at the point (1,-2) in the direction of the unit vector :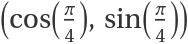

In[1]:=

$ResourceFunction["DirectionalDerivative"][ x y - x^2 - y^3, {x, y}, {1, -2}, {Cos[\[Pi]/4], Sin[\[Pi]/4]}]$

Out[1]=

The directional derivative of the same function at a general point (a,b) in a general direction (cos(α),sin(α)):

In[2]:=

$ResourceFunction["DirectionalDerivative"][ x y - x^2 - y^3, {x, y}, {a, b}, {Cos[\[Alpha]], Sin[\[Alpha]]}]$

Out[2]=

Scope (6)

Find the directional derivative of a function of four variables:

In[3]:=

$ResourceFunction["DirectionalDerivative"][ Sin[x y z w], {x, y, z, w}, {\[Pi], 1, 3, 2}, {1, 2, -1, -2}]$

Out[3]=

Since the following function is not differentiable at (0,0), it is necessary to use the limit definition to correctly calculate the directional derivative:

In[4]:=

$Clear[f] f[x_, y_] := \!\(\* TagBox[GridBox[{ {"\[Piecewise]", GridBox[{ { FractionBox[ RowBox[{ SuperscriptBox["x", "2"], " ", "y"}], RowBox[{ SuperscriptBox["x", "2"], "+", SuperscriptBox["y", "2"]}]], RowBox[{ RowBox[{"{", RowBox[{"x", ",", "y"}], "}"}], "!=", RowBox[{"{", RowBox[{"0", ",", "0"}], "}"}]}]}, {"0", "True"} }, AllowedDimensions->{2, Automatic}, Editable->True, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, "Rows" -> {{1.}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.84]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}, Selectable->True]} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, "Rows" -> {{1.}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.35]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "Piecewise", DeleteWithContents->True, Editable->False, SelectWithContents->True, Selectable->False, StripWrapperBoxes->True]\) ResourceFunction["DirectionalDerivative"][ f[x, y], {x, y}, {0, 0}, {2, 1}, "UseLimit" -> True]$

Out[5]=

Calculate the gradient of this function at the origin:

In[6]:=

$Clear[f] f[x_, y_] := \!\(\* TagBox[GridBox[{ {"\[Piecewise]", GridBox[{ { FractionBox[ RowBox[{ SuperscriptBox["x", "2"], " ", "y"}], RowBox[{ SuperscriptBox["x", "2"], "+", SuperscriptBox["y", "2"]}]], RowBox[{ RowBox[{"{", RowBox[{"x", ",", "y"}], "}"}], "!=", RowBox[{"{", RowBox[{"0", ",", "0"}], "}"}]}]}, {"0", "True"} }, AllowedDimensions->{2, Automatic}, Editable->True, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, "Rows" -> {{1.}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.84]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}, Selectable->True]} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, "Rows" -> {{1.}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.35]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "Piecewise", DeleteWithContents->True, Editable->False, SelectWithContents->True, Selectable->False, StripWrapperBoxes->True]\) ResourceFunction["DirectionalDerivative"][f[x, y], {x, y}, {0, 0}, #, "UseLimit" -> True] & /@ {{1, 0}, {0, 1}}$

Out[7]=

The gradient can also be calculated using the resource function EnhancedGrad:

In[8]:=

Out[8]=

Since the gradient of this function at (0,0) is (0,0), without setting "UseLimit"->True, the formula 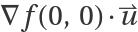returns 0 no matter the direction :

In[9]:=

Out[10]=

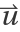A function that does not have a directional derivative except in the x and y directions:

In[11]:=

$Clear[f] f[x_, y_] := \!\(\* TagBox[GridBox[{ {"\[Piecewise]", GridBox[{ { FractionBox[ RowBox[{"x", " ", "y"}], RowBox[{ SuperscriptBox["x", "2"], "+", SuperscriptBox["y", "2"]}]], RowBox[{ RowBox[{"{", RowBox[{"x", ",", "y"}], "}"}], "!=", RowBox[{"{", RowBox[{"0", ",", "0"}], "}"}]}]}, {"0", "True"} }, AllowedDimensions->{2, Automatic}, Editable->True, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, "Rows" -> {{1.}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.84]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}, Selectable->True]} }, GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "ColumnsIndexed" -> {}, "Rows" -> {{1.}}, "RowsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.35]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}}], "Piecewise", DeleteWithContents->True, Editable->False, SelectWithContents->True, Selectable->False, StripWrapperBoxes->True]\) {ResourceFunction["DirectionalDerivative"][f[x, y], {x, y}, {0, 0}, #, "UseLimit" -> True] & /@ {{1, 0}, {0, 1}}, ResourceFunction["DirectionalDerivative"][ f[x, y], {x, y}, {0, 0}, {Cos[\[Alpha]], Sin[\[Alpha]]}, "UseLimit" -> True]}$

Out[12]=

A function requiring both "UseLimit" and "UseRealRoots":

In[13]:=

$Clear[f] f[x_, y_] := (x^2 y)^(1/3) ResourceFunction["DirectionalDerivative"][ f[x, y], {x, y}, {0, 0}, {1, -1}, "UseLimit" -> True] // ResourceFunction["UseRealRoots"]$

Out[3]=