Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the directional derivative of a function
ResourceFunction["DirectionalD"][f,r,vars] computes the derivative of a function f in the direction r with variables vars. |
Directional derivative of a function of two variables:
| In[1]:= |
| Out[1]= |
Directional derivative of a function of three variables:
| In[2]:= |
| Out[2]= |
Directional derivative with a zero component in one direction:
| In[3]:= |
| Out[3]= |
A unit vector along direction (3/2,1):
| In[4]:= |
| Out[4]= |
Without normalization:
| In[5]:= |
| Out[5]= |
Evaluated at the point p=(3/2,1):
| In[6]:= |
| Out[6]= |
Define a function:
| In[7]:= |
Compute the directional derivative:
| In[8]:= |
| Out[8]= |
Directional derivative in the direction (-1,-1/2) evaluated at the point (-1,3/2):
| In[9]:= |
| Out[9]= |
A plot of the directional derivative:
| In[10]:= | ![With[{p = {x, y, 3 x^2 y} /. {x -> -1, y -> 3/2}}, Show[Plot3D[3 x^2 y, {x, -2, 0}, {y, 0, 2}, Mesh -> None, PlotStyle -> Opacity[.5]], Graphics3D[{Red, Point[p], Arrowheads[.005], Arrow[{p, p + .5 {-1, -(1/2), 15/2}}]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/029/0293a41a-50cc-4aa0-9980-fecbace738f2/19bddab60f8b2457.png) |
| Out[10]= | 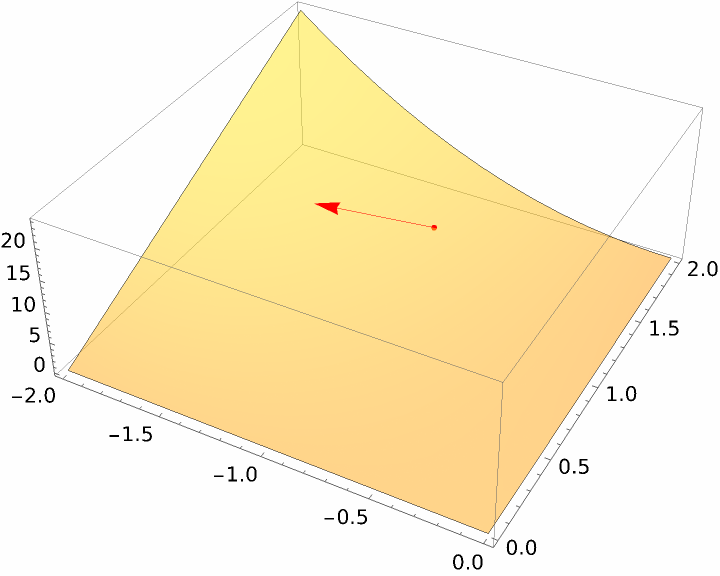 |
Visualize directional derivatives over a surface:
| In[11]:= | ![arrows = With[{d = {.5, 1}}, Graphics3D[{Arrowheads[.025], Table[Arrow[{{x0, y0, Sin[x0] Cos[y0]}, {x0, y0, Sin[x0] Cos[y0]} + .5 Normalize[{d[[1]], d[[2]], ResourceFunction["DirectionalD"][Sin[x] Cos[y], d, {x, y}] /. {x -> x0, y -> y0}}]}], {x0, 0, 5, .5}, {y0, 0, 5, .5}]}]];
Show[Plot3D[Sin[x] Cos[y], {x, 0, 5.5}, {y, 0, 5.5}, Mesh -> None, PlotStyle -> Opacity[.5]], arrows]](https://www.wolframcloud.com/obj/resourcesystem/images/029/0293a41a-50cc-4aa0-9980-fecbace738f2/7b821d4e6a65809e.png) |
| Out[12]= | 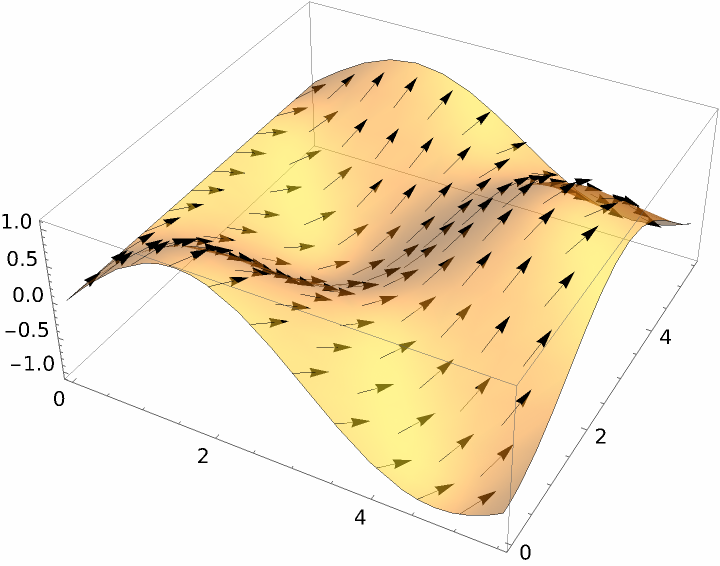 |
The directional derivative (red) and the gradient (blue):
| In[13]:= | ![Manipulate[
With[{pt2 = Append[pt, 2 x^2 - y^2] /. Thread[{x, y} -> pt]}, Show[Plot3D[2 x^2 - y^2, {x, -5, 5}, {y, -5, 5}, Mesh -> None, PerformanceGoal -> "Quality", PlotStyle -> Opacity[.5], PlotRange -> {{-5, 5}, {-5, 5}, {-26, 51}}], Graphics3D[{Arrowheads[.005], Blue, Arrow[{pt2, pt2 + {1, 1, 4 x - 2 y}}], Red, Arrow[{pt2, pt2 + {a, b, Normalize[
ResourceFunction["DirectionalD"][
2 x^2 - y^2, {a, b}, {x, y}]]}}]} /. Thread[{x, y} -> pt]]]],
{{pt, {2, -2}}, {-4, -4}, {4, 4}}, {a, -1, 1}, {b, -1, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/029/0293a41a-50cc-4aa0-9980-fecbace738f2/303485e88066d8e5.png) |
| Out[13]= | 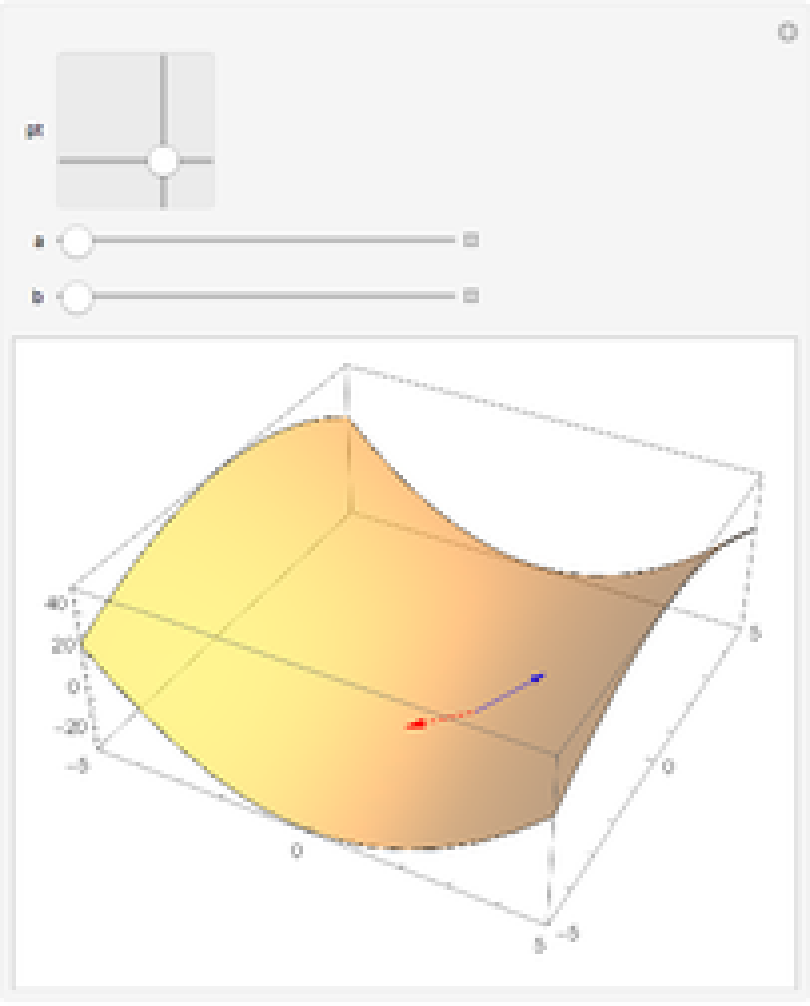 |
This work is licensed under a Creative Commons Attribution 4.0 International License