Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
DirectedGraph
Obtain partial probabilities of random walks on a directed graph
Contributed by:
Bradley Klee
ResourceFunction["DirectedGraphTransferMatrix"][g] returns a matrix whose elements are partial probabilities describing random walks across directed graph g. | |
ResourceFunction["DirectedGraphTransferMatrix"][g,outs,ins] orders the rows and columns of the output matrix according to vertex lists outs and ins. |
Details
A random walk across directed graph g starts at one particular input vertex (VertexInDegree = 0) and ends at one particular output vertex (VertexOutDegree = 0). On all intermediary nodes, the walk chooses a next step at random from the immediate out components. If edge weights are specified, the random choice is weighted by the specified values.
The default ordering of the row and column spaces follows the ordering of VertexList, with output vertices on rows and input vertices on columns. It may be counter-intuitive to have outs before ins in the argument sequence. The reason behind this convention is that the row index goes before column index in Part specification.
On graphs with loops, intermediary vertices can have matrix elements greater than one. Such values indicate that a random walk can be expected to visit a particular vertex more than once before terminating on an output.
Vertex lists outs and ins are not only useful for re-ordering, but also for selecting matrix subspaces or particular elements.
ResourceFunction["DirectedGraphTransferMatrix"] accepts one option "Throughput" whose default value is False. When "Throughput" is set to True, the return matrix has extra rows listing partial probabilities on intermediary vertices.
With the setting "Throughput"→False, columns of the transfer matrix must sum to one by conservation of probability. This property does not depend on edge weights, because edge weights are assumed relative and normalized separately on each vertex.
Examples
Basic Examples (4)
Find the transfer matrix for a simple directed graph with one loop:
| In[1]:= | ![ResourceFunction["DirectedGraphTransferMatrix"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {3, 2}, {3, 4}, {2, 5}, {6, 3}}, Null}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJxTTMoPSmViYGBQA2IQzWD4rfbRC2aHJ1fnBzjwf7EXsdl9do30X3vHJL/z
Ozmf2HswrnXb2fnU/lTJAR0XIJ/BoTQwcbaZ/RMfM8MDzF/sZXKa/ii/Z3Zg
QAcuJkub+SLsd22863BD+7e96xpNkenrHtnbXVaKyVv7y36Zzn/N2zGP7F/a
Hn9mpPvLftNtLat48Uf29wyDzhau/mnv8GJKhs+9h/Yp7/4+Ktf4aX9oNUfD
kY0P7YMkrLdMWvLD/ugGo3sPJz60tyk/FiGg8MN+QzhLyva6h/ZfLHJc7Wd/
t78Q3pYVUPHQPilkVXqQ6wf7Kz82xygC+Qp5S+qZGt/bK8T4rWsEql9n+sD3
b/k7+4/vO1uWAs2bKfFS2ajgrf2vOp+uRqB9Aps2GtpmvbGf2dj3iAnonllx
RybsTHttP9m7zZgf6N64oLwXDmmv7AOknLa1AP0z7elRoezMl/aXji33sgL6
979oRkISkH9c6+nztJSn9j8v3dU0A6pPX8V/SWnbU/uFf6eIrAWaF/X78cF5
v5/a7xStd9cH2nf2XeXkjSbP7NfMUZdRBrrHS5utxjLxmf0Fj7WVb4HudVO7
IyvT+Mz+d9c0g08N7+2j67lmuE15Zn+seam2F9C/NvUdE9fOemYfkZHOaQ4M
D4t7UfPvAPmrWu0NOYDh9bbqgG8NUP3jhYqnuoDhKfO8pTwCaF6egWx8ATC8
hSIOFdYA7dv02OJGFjA+ikIbJH8D3ZPbu36FDjC+Krs7TrwDurd78q0/GcD4
3L3njGsl0D/vT657fhkY31YC6RsPA/0LAFK3LZg=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{1, 2}, 0.02648044255408355], ArrowBox[
BezierCurveBox[{2, {1.246168511228847, 0.43767808839853345`}, 3}], 0.02648044255408355], ArrowBox[{2, 5}, 0.02648044255408355], ArrowBox[
BezierCurveBox[{3, {1.246150063368406, 0.8146402865220455}, 2}], 0.02648044255408355], ArrowBox[{3, 4}, 0.02648044255408355], ArrowBox[{6, 3}, 0.02648044255408355]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02648044255408355], DiskBox[2, 0.02648044255408355], DiskBox[3, 0.02648044255408355], DiskBox[4, 0.02648044255408355], DiskBox[5, 0.02648044255408355], DiskBox[6, 0.02648044255408355]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/77df0d3c1f521c96.png) |
| Out[1]= |  |
The probability for a random-walk to go from vertex 5 to vertex 3:
| In[2]:= | ![ResourceFunction["DirectedGraphTransferMatrix"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {3, 2}, {3, 4}, {2, 5}, {6, 3}}, Null}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{2.488713249278703, 1.2537234448803867`}, {
1.8192565952665563`, 0.6261872338246307}}, 0.02648044255408355], ArrowBox[
BezierCurveBox[{{1.8192565952665563`, 0.6261872338246307}, {1.246168511228847, 0.43767808839853345`}, {0.6730619793307051, 0.6261311410959476}}], 0.02648044255408355], ArrowBox[{{1.8192565952665563`, 0.6261872338246307}, {
2.4917678572942474`, 0.}}, 0.02648044255408355], ArrowBox[
BezierCurveBox[{{0.6730619793307051, 0.6261311410959476}, {
1.246150063368406, 0.8146402865220455}, {
1.8192565952665563`, 0.6261872338246307}}], 0.02648044255408355], ArrowBox[{{0.6730619793307051, 0.6261311410959476}, {
0.0003449547379732465, 1.2509157106731488`}}, 0.02648044255408355], ArrowBox[{{0., 0.0014683042143739389`}, {0.6730619793307051,
0.6261311410959476}}, 0.02648044255408355]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{2.488713249278703, 1.2537234448803867`}, 0.02648044255408355], InsetBox["0", Offset[{2, 2}, {2.5151936918327866, 1.2802038874344701}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.8192565952665563`, 0.6261872338246307}, 0.02648044255408355], InsetBox["1", Offset[{2, 2}, {1.8457370378206397, 0.6526676763787143}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.6730619793307051, 0.6261311410959476}, 0.02648044255408355], InsetBox["2", Offset[{2, 2}, {0.6995424218847887, 0.6526115836500311}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.0003449547379732465, 1.2509157106731488`}, 0.02648044255408355], InsetBox["3", Offset[{2, 2}, {0.026825397292056796, 1.2773961532272322}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.4917678572942474`, 0.}, 0.02648044255408355], InsetBox["4", Offset[{2, 2}, {2.518248299848331, 0.02648044255408355}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.0014683042143739389`}, 0.02648044255408355],
InsetBox["5", Offset[{2, 2}, {0.02648044255408355, 0.02794874676845749}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None]\), {3}, {5}]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/240472fd4f55913c.png) |
| Out[2]= |  |
Determine output probabilities from input probabilities using Dot:
| In[3]:= | ![ResourceFunction["DirectedGraphTransferMatrix"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {3, 2}, {3, 4}, {2, 5}, {6, 3}}, Null}, {FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{2.488713249278703, 1.2537234448803867`}, {
1.8192565952665563`, 0.6261872338246307}}, 0.02648044255408355], ArrowBox[
BezierCurveBox[{{1.8192565952665563`, 0.6261872338246307}, {1.246168511228847, 0.43767808839853345`}, {0.6730619793307051, 0.6261311410959476}}], 0.02648044255408355], ArrowBox[{{1.8192565952665563`, 0.6261872338246307}, {
2.4917678572942474`, 0.}}, 0.02648044255408355], ArrowBox[
BezierCurveBox[{{0.6730619793307051, 0.6261311410959476}, {1.246150063368406, 0.8146402865220455}, {1.8192565952665563`, 0.6261872338246307}}], 0.02648044255408355], ArrowBox[{{0.6730619793307051, 0.6261311410959476}, {
0.0003449547379732465, 1.2509157106731488`}}, 0.02648044255408355], ArrowBox[{{0., 0.0014683042143739389`}, {
0.6730619793307051, 0.6261311410959476}}, 0.02648044255408355]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{2.488713249278703, 1.2537234448803867`}, 0.02648044255408355], InsetBox["0", Offset[{2, 2}, {2.5151936918327866, 1.2802038874344701}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.8192565952665563`, 0.6261872338246307}, 0.02648044255408355], InsetBox["1", Offset[{2, 2}, {1.8457370378206397, 0.6526676763787143}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.6730619793307051, 0.6261311410959476}, 0.02648044255408355], InsetBox["2", Offset[{2, 2}, {0.6995424218847887, 0.6526115836500311}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.0003449547379732465, 1.2509157106731488`}, 0.02648044255408355], InsetBox["3", Offset[{2, 2}, {0.026825397292056796, 1.2773961532272322}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.4917678572942474`, 0.}, 0.02648044255408355], InsetBox["4", Offset[{2, 2}, {2.518248299848331, 0.02648044255408355}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.0014683042143739389`}, 0.02648044255408355], InsetBox["5", Offset[{2, 2}, {0.02648044255408355, 0.02794874676845749}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None]\), {3, 4}, {0, 5}] . {1/3, 2/3}](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/5356eb4b12c929ec.png) |
| Out[3]= |  |
Label a binary tree with its output probabilities:
| In[4]:= | ![Module[{g0 = KaryTree[10, DirectedEdges -> True], outs},
outs = Select[VertexList[g0], VertexOutDegree[g0, #] == 0 &];
Graph[g0, VertexLabels -> MapThread[
#1 -> Placed[#2, {-1.5, 0}] &,
{outs, Catenate[
ResourceFunction["DirectedGraphTransferMatrix"][g0]
]}]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/3ab6b8044d24430f.png) |
| Out[4]= |  |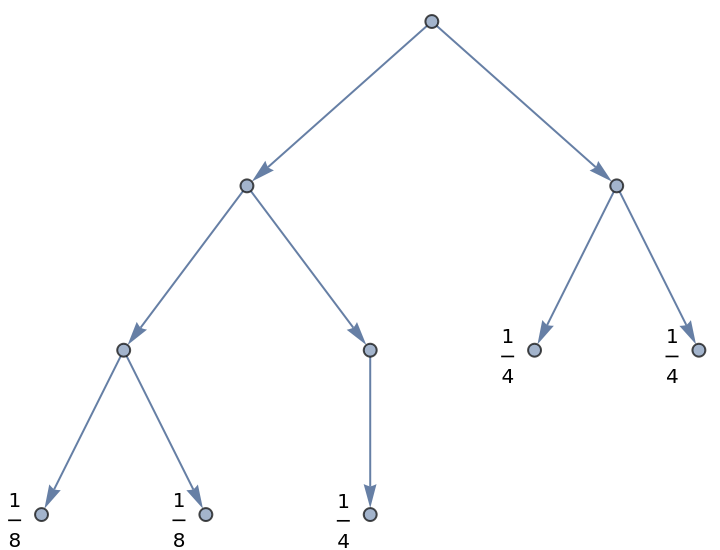
Scope (1)
Adding edge weights to a graph changes the elements of the transfer matrix:
| In[5]:= | ![ResourceFunction["DirectedGraphTransferMatrix"][Graph[\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{0, 1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {3, 2}, {3, 4}, {2, 5}, {6, 3}}, Null}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJxTTMoPSmViYGBQA2IQzWD4rfbRC2aHJ1fnBzjwf7EXsdl9do30X3vHJL/z
Ozmf2HswrnXb2fnU/lTJAR0XIJ/BoTQwcbaZ/RMfM8MDzF/sZXKa/ii/Z3Zg
QAcuJkub+SLsd22863BD+7e96xpNkenrHtnbXVaKyVv7y36Zzn/N2zGP7F/a
Hn9mpPvLftNtLat48Uf29wyDzhau/mnv8GJKhs+9h/Yp7/4+Ktf4aX9oNUfD
kY0P7YMkrLdMWvLD/ugGo3sPJz60tyk/FiGg8MN+QzhLyva6h/ZfLHJc7Wd/
t78Q3pYVUPHQPilkVXqQ6wf7Kz82xygC+Qp5S+qZGt/bK8T4rWsEql9n+sD3
b/k7+4/vO1uWAs2bKfFS2ajgrf2vOp+uRqB9Aps2GtpmvbGf2dj3iAnonllx
RybsTHttP9m7zZgf6N64oLwXDmmv7AOknLa1AP0z7elRoezMl/aXji33sgL6
979oRkISkH9c6+nztJSn9j8v3dU0A6pPX8V/SWnbU/uFf6eIrAWaF/X78cF5
v5/a7xStd9cH2nf2XeXkjSbP7NfMUZdRBrrHS5utxjLxmf0Fj7WVb4HudVO7
IyvT+Mz+d9c0g08N7+2j67lmuE15Zn+seam2F9C/NvUdE9fOemYfkZHOaQ4M
D4t7UfPvAPmrWu0NOYDh9bbqgG8NUP3jhYqnuoDhKfO8pTwCaF6egWx8ATC8
hSIOFdYA7dv02OJGFjA+ikIbJH8D3ZPbu36FDjC+Krs7TrwDurd78q0/GcD4
3L3njGsl0D/vT657fhkY31YC6RsPA/0LAFK3LZg=
"], {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{1, 2}, 0.02648044255408355], ArrowBox[
BezierCurveBox[{2, {1.246168511228847, 0.43767808839853345`}, 3}], 0.02648044255408355], ArrowBox[{2, 5}, 0.02648044255408355], ArrowBox[
BezierCurveBox[{3, {1.246150063368406, 0.8146402865220455}, 2}], 0.02648044255408355], ArrowBox[{3, 4}, 0.02648044255408355], ArrowBox[{6, 3}, 0.02648044255408355]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02648044255408355], DiskBox[2, 0.02648044255408355], DiskBox[3, 0.02648044255408355], DiskBox[4, 0.02648044255408355], DiskBox[5, 0.02648044255408355], DiskBox[6, 0.02648044255408355]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None]\),
EdgeWeight -> {
DirectedEdge[1, 2] -> 2,
DirectedEdge[2, 1] -> 3
}]]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/2aa2d8dab3d07823.png) |
| Out[5]= |  |
Options (1)
Throughput (1)
Label a binary tree with all of its partial probabilities:
| In[6]:= | ![Module[{g0 = KaryTree[10, DirectedEdges -> True], vertices},
vertices = Select[VertexList[g0], VertexInDegree[g0, #] != 0 &];
Graph[g0, VertexLabels -> Append[MapThread[
#1 -> Placed[#2, {-1.5, 0}] &,
{vertices, Catenate[
ResourceFunction["DirectedGraphTransferMatrix"][
g0, "Throughput" -> True]
]}], 1 -> 1]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/1897a4690742af3d.png) |
| Out[6]= |  |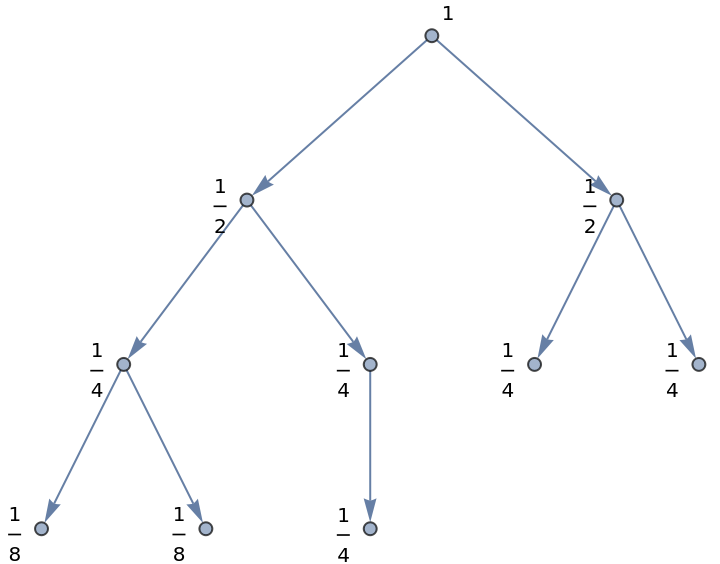
Properties and Relations (4)
Columns of the transfer matrix sum to 1:
| In[7]:= | ![With[{seed = SeedRandom[123],
graph = First[WeaklyConnectedGraphComponents[
RandomGraph[{80, 100}, DirectedEdges -> True]]]},
Labeled[graph,
Total[ResourceFunction["DirectedGraphTransferMatrix"][
graph]]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/7e5b2a3a48e9cc83.png) |
| Out[7]= |  |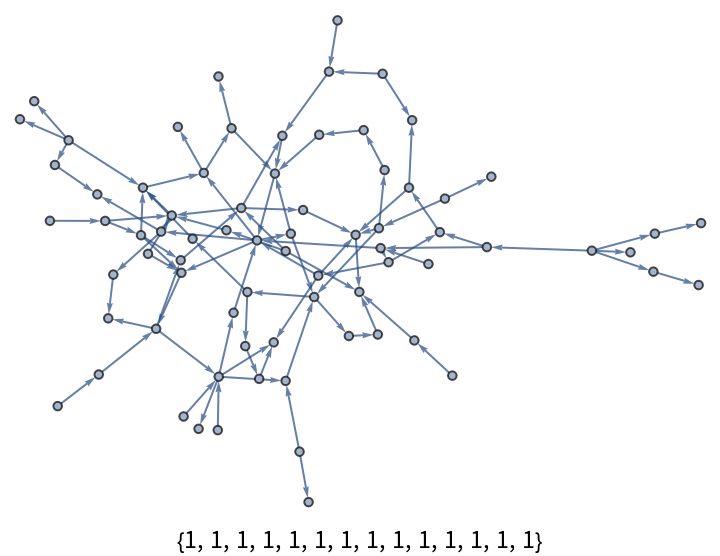
The column sum property does not depend on edge weights:
| In[8]:= | ![Module[{seed = SeedRandom[123],
graph = First[WeaklyConnectedGraphComponents[
RandomGraph[{80, 100}, DirectedEdges -> True]]]},
graph = Graph[graph, EdgeWeight -> Map[
# -> RandomInteger[{1, 5}] &,
EdgeList[graph]
]];
Labeled[graph,
MinMax[WeightedAdjacencyMatrix[graph]] -> Total[ResourceFunction["DirectedGraphTransferMatrix"][
graph]]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/18156b0383943e05.png) |
| Out[8]= |  |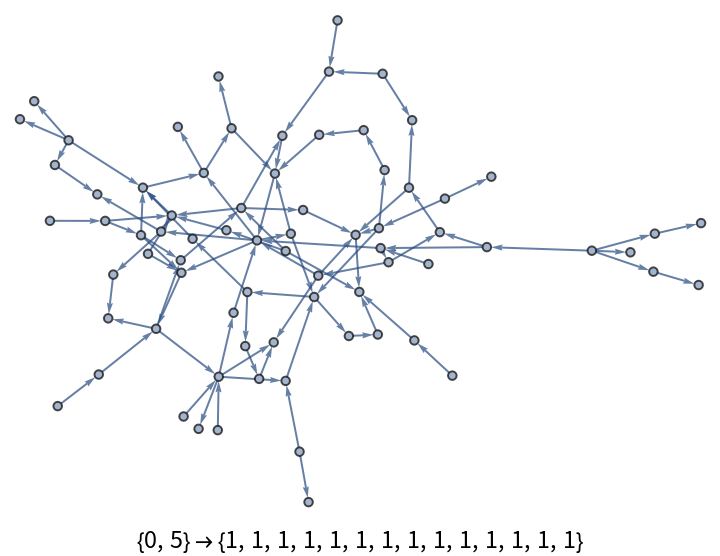
Check the continuity constraint on each element of the transfer matrix:
| In[9]:= | ![Module[{seed = SeedRandom[321], graph, res, vertices, ins, weights, inits, check},
graph = First[WeaklyConnectedGraphComponents[
RandomGraph[{80, 100}, DirectedEdges -> True]]];
res = ResourceFunction["DirectedGraphTransferMatrix"][
graph, "Throughput" -> True];
vertices = Select[VertexList[graph], VertexInDegree[graph, #] != 0 &];
inits = Select[VertexList[graph], VertexInDegree[graph, #] == 0 &];
inits = Association[MapThread[Rule, {inits, IdentityMatrix[Length[inits]]}]];
ins = VertexInComponent[graph, #, {1}] & /@ vertices;
weights = Map[VertexOutDegree[graph, #] &, ins, {2}];
vertices = Association[MapIndexed[#1 -> #2[[1]] &, vertices]];
Labeled[graph,
SameQ[Total /@ MapThread[Function[{in, weight},
MapThread[
If[TrueQ[Lookup[vertices, #1, True]],
inits[#1], res[[vertices[#1]]]
]/#2 &, {in, weight}]
], {ins, weights}
],
res]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/6a0e53f68dae6cb8.png) |
| Out[9]= |  |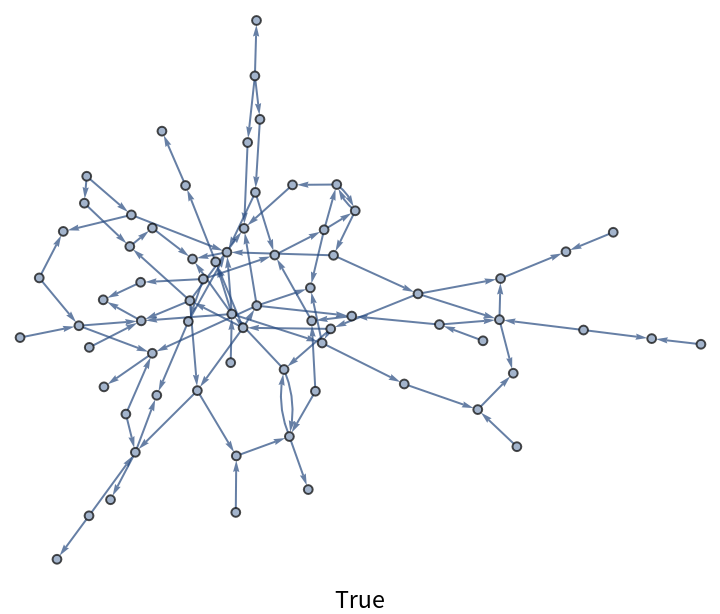
On graphs with cycles, throughput vertices can have partial probabilities greater than one:
| In[10]:= | ![g0 = Graph[{1 -> 2, 2 -> 1, 0 -> 1, 1 -> 4}]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/512590dd980f1e8b.png){kind=small} |
| Out[10]= |  |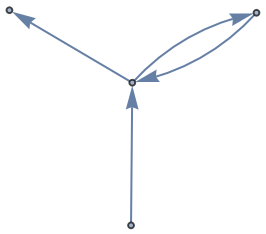
| In[11]:= | ![ResourceFunction["DirectedGraphTransferMatrix"][g0, {1}, {0}, "Throughput" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/32b11fa642329c70.png){kind=small} |
| Out[11]= |  |
This means that, on average, the random walk will go through loops to visit the same vertex more than once:
| In[12]:= | ![Module[{graph, edgeList, res},
SeedRandom[123];
edgeList = GroupBy[EdgeList[g0], First -> Last];
N[Mean@Table[
Count[FixedPointList[RandomChoice[
Lookup[edgeList, Key[#], {True}]] &, 0], 1],
100000
]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/46d7fa147f79b9c4.png) |
| Out[12]= |  |
Possible Issues (2)
Calculations may fail due to trapped cycles:
| In[13]:= | ![With[{seed = SeedRandom[123],
g0 = RandomGraph[{10, 12},
DirectedEdges -> True]},
g0 -> ResourceFunction["DirectedGraphTransferMatrix"][g0]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/6fc9f29928f07452.png) |
| Out[13]= |  |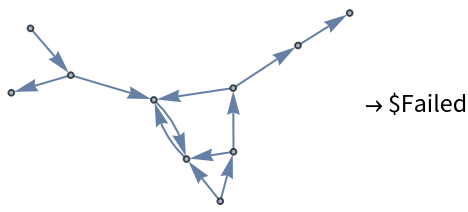
Adding an extra edge allows a positive result:
| In[14]:= | ![With[{seed = SeedRandom[123],
g0 = EdgeAdd[RandomGraph[{10, 12},
DirectedEdges -> True], {2 -> 0}]},
Row[{Graph[g0, ImageSize -> 200],
Style["\[RightArrow]", Gray, Bold, 24], MatrixForm[
ResourceFunction["DirectedGraphTransferMatrix"][g0]
]}, Spacer[10]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/07876e0221482945.png) |
| Out[14]= |  |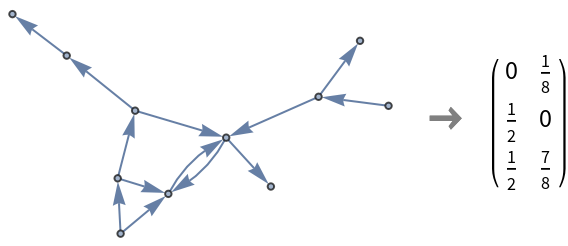
Neat Examples (2)
Find the probability of solving a logic maze through a random walk, without hitting a dead end:
| In[15]:= | ![With[{maze = Graph[{{5, 2,
RGBColor[1, 0, 0]}, {4, 2,
GrayLevel[0.5]}, {3, 2,
RGBColor[0, 0, 1]}, {3, 3,
RGBColor[1, 0, 0]}, {2, 3,
GrayLevel[0.5]}, {3, 4,
GrayLevel[0.5]}, {2, 2,
RGBColor[0, 0, 1]}, {4, 4,
RGBColor[0, 0, 1]}, {2, 1,
RGBColor[1, 0, 0]}, {4, 3,
RGBColor[1, 0, 0]}, {1, 1,
GrayLevel[0.5]}, {3, 1,
GrayLevel[0.5]}, {4, 1,
RGBColor[0, 0, 1]}, {4, 2,
RGBColor[1, 0, 0]}, {4, 3,
GrayLevel[0.5]}, {5, 2,
GrayLevel[0.5]}, {3, 3,
RGBColor[0, 0, 1]}, {3, 2,
RGBColor[1, 0, 0]}, {2, 2,
GrayLevel[0.5]}, {1, 2,
RGBColor[0, 0, 1]}, {2, 3,
RGBColor[0, 0, 1]}, {1, 1,
RGBColor[1, 0, 0]}, {1, 3,
RGBColor[1, 0, 0]}, {2, 4,
RGBColor[1, 0, 0]}, {2, 1,
GrayLevel[0.5]}, {1, 2,
GrayLevel[0.5]}, {1, 4,
GrayLevel[0.5]}, {1, 3,
RGBColor[0, 0, 1]}, {2, 3,
RGBColor[1, 0, 0]}, {3, 3,
GrayLevel[0.5]}, {4, 3,
RGBColor[0, 0, 1]}, {4, 4,
RGBColor[1, 0, 0]}, {5, 3,
RGBColor[1, 0, 0]}}, {{{1, 2}, {2, 3}, {3, 4}, {4, 5}, {4, 6}, {5, 7}, {6, 8}, {7, 9}, {8, 10}, {9, 11}, {9, 12}, {10, 2}, {12, 3}, {12, 13}, {13, 14}, {14, 15}, {14, 16}, {15, 17}, {17, 18}, {
18, 19}, {19, 20}, {19, 21}, {20, 22}, {21, 23}, {21, 24}, {22, 25}, {23, 26}, {24, 27}, {24, 6}, {26, 7}, {27, 28}, {28, 29}, {
29, 30}, {30, 31}, {31, 32}, {31, 33}}, Null}, {EdgeStyle -> {
RGBColor[0.6666666666666666, 0.6666666666666666, 0.6666666666666666]},
FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 3, "VertexLayout" -> {"LayeredEmbedding", "RootVertex" -> {5, 2,
RGBColor[1, 0, 0]}}}, VertexCoordinates -> {{2, -5, 0}, {2, -4,
Rational[1, 3]}, {2, -3,
Rational[-1, 3]}, {3, -3, 0}, {3, -2,
Rational[1, 3]}, {4, -3,
Rational[1, 3]}, {2, -2,
Rational[-1, 3]}, {4, -4,
Rational[-1, 3]}, {1, -2, 0}, {3, -4, 0}, {1, -1,
Rational[1, 3]}, {1, -3,
Rational[1, 3]}, {1, -4,
Rational[-1, 3]}, {2, -4, 0}, {3, -4,
Rational[1, 3]}, {2, -5,
Rational[1, 3]}, {3, -3,
Rational[-1, 3]}, {2, -3, 0}, {2, -2,
Rational[1, 3]}, {2, -1,
Rational[-1, 3]}, {3, -2,
Rational[-1, 3]}, {1, -1, 0}, {3, -1, 0}, {4, -2, 0}, {1, -2,
Rational[1, 3]}, {2, -1,
Rational[1, 3]}, {4, -1,
Rational[1, 3]}, {3, -1,
Rational[-1, 3]}, {3, -2, 0}, {3, -3,
Rational[1, 3]}, {3, -4,
Rational[-1, 3]}, {4, -4, 0}, {3, -5, 0}}, VertexStyle -> {
Directive[
EdgeForm[
GrayLevel[0.5]],
GrayLevel[0.85]], {3, 3,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {3, 4,
GrayLevel[0.5]} -> GrayLevel[0.5], {4, 3,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {3, 2,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {3, 1,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 1,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {3, 3,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 4,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 2,
GrayLevel[0.5]} -> GrayLevel[0.5], {4, 3,
GrayLevel[0.5]} -> GrayLevel[0.5], {2, 3,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {4, 1,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {4, 4,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {3, 2,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {4, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {3, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {4, 2,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {5, 2,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {2, 1,
GrayLevel[0.5]} -> GrayLevel[0.5], {2, 2,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {2, 3,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {2, 4,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {4, 2,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 3,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {2, 1,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {1, 1,
GrayLevel[0.5]} -> GrayLevel[0.5], {2, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {1, 2,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {4, 4,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {5, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {2, 2,
GrayLevel[0.5]} -> GrayLevel[0.5], {5, 2,
GrayLevel[0.5]} -> GrayLevel[0.5]}}]},
Labeled[Show[maze,
ViewVertical -> {0, 0, 1},
ViewPoint -> {5, 3, 5},
Lighting -> {{"Ambient", White}}],
"Probability" -> ResourceFunction["DirectedGraphTransferMatrix"][
maze, {{5, 3, RGBColor[1, 0, 0]}}, {{5, 2, RGBColor[1, 0, 0]}}][[
1, 1]]
]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/0fe1e2eb363f4055.png) |
| Out[15]= |  |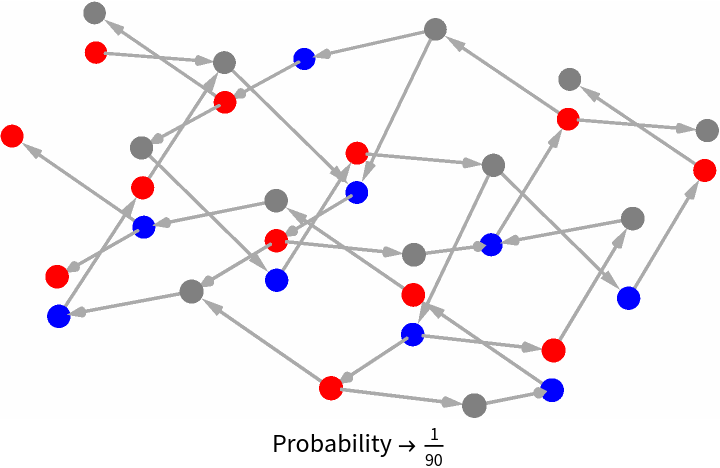
Compare with brute force enumeration of 100,000 random walks:
| In[16]:= | ![Module[{edgeList, res},
SeedRandom[123];
edgeList = GroupBy[EdgeList[
Graph[{{5, 2,
RGBColor[1, 0, 0]}, {4, 2,
GrayLevel[0.5]}, {3, 2,
RGBColor[0, 0, 1]}, {3, 3,
RGBColor[1, 0, 0]}, {2, 3,
GrayLevel[0.5]}, {3, 4,
GrayLevel[0.5]}, {2, 2,
RGBColor[0, 0, 1]}, {4, 4,
RGBColor[0, 0, 1]}, {2, 1,
RGBColor[1, 0, 0]}, {4, 3,
RGBColor[1, 0, 0]}, {1, 1,
GrayLevel[0.5]}, {3, 1,
GrayLevel[0.5]}, {4, 1,
RGBColor[0, 0, 1]}, {4, 2,
RGBColor[1, 0, 0]}, {4, 3,
GrayLevel[0.5]}, {5, 2,
GrayLevel[0.5]}, {3, 3,
RGBColor[0, 0, 1]}, {3, 2,
RGBColor[1, 0, 0]}, {2, 2,
GrayLevel[0.5]}, {1, 2,
RGBColor[0, 0, 1]}, {2, 3,
RGBColor[0, 0, 1]}, {1, 1,
RGBColor[1, 0, 0]}, {1, 3,
RGBColor[1, 0, 0]}, {2, 4,
RGBColor[1, 0, 0]}, {2, 1,
GrayLevel[0.5]}, {1, 2,
GrayLevel[0.5]}, {1, 4,
GrayLevel[0.5]}, {1, 3,
RGBColor[0, 0, 1]}, {2, 3,
RGBColor[1, 0, 0]}, {3, 3,
GrayLevel[0.5]}, {4, 3,
RGBColor[0, 0, 1]}, {4, 4,
RGBColor[1, 0, 0]}, {5, 3,
RGBColor[1, 0, 0]}}, {{{1, 2}, {2, 3}, {3, 4}, {4, 5}, {4, 6}, {5, 7}, {6, 8}, {7, 9}, {8, 10}, {9, 11}, {9, 12}, {10, 2}, {12, 3}, {12, 13}, {13, 14}, {14, 15}, {14, 16}, {15, 17}, {17, 18}, {18, 19}, {19, 20}, {19, 21}, {20, 22}, {21, 23}, {21, 24}, {22, 25}, {23, 26}, {24, 27}, {24, 6}, {26, 7}, {27, 28}, {
28, 29}, {29, 30}, {30, 31}, {31, 32}, {31, 33}}, Null}, {EdgeStyle -> {
RGBColor[0.6666666666666666, 0.6666666666666666, 0.6666666666666666]},
FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 3, "VertexLayout" -> {"LayeredEmbedding", "RootVertex" -> {5, 2,
RGBColor[1, 0, 0]}}}, VertexCoordinates -> {{2, -5, 0}, {2, -4,
Rational[1, 3]}, {2, -3,
Rational[-1, 3]}, {3, -3, 0}, {3, -2,
Rational[1, 3]}, {4, -3,
Rational[1, 3]}, {2, -2,
Rational[-1, 3]}, {4, -4,
Rational[-1, 3]}, {1, -2, 0}, {3, -4, 0}, {1, -1,
Rational[1, 3]}, {1, -3,
Rational[1, 3]}, {1, -4,
Rational[-1, 3]}, {2, -4, 0}, {3, -4,
Rational[1, 3]}, {2, -5,
Rational[1, 3]}, {3, -3,
Rational[-1, 3]}, {2, -3, 0}, {2, -2,
Rational[1, 3]}, {2, -1,
Rational[-1, 3]}, {3, -2,
Rational[-1, 3]}, {1, -1, 0}, {3, -1, 0}, {4, -2, 0}, {1, -2,
Rational[1, 3]}, {2, -1,
Rational[1, 3]}, {4, -1,
Rational[1, 3]}, {3, -1,
Rational[-1, 3]}, {3, -2, 0}, {3, -3,
Rational[1, 3]}, {3, -4,
Rational[-1, 3]}, {4, -4, 0}, {3, -5, 0}}, VertexStyle -> {
Directive[
EdgeForm[
GrayLevel[0.5]],
GrayLevel[0.85]], {3, 3,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {3, 4,
GrayLevel[0.5]} -> GrayLevel[0.5], {4, 3,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {3, 2,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {3, 1,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 1,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {3, 3,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 4,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 2,
GrayLevel[0.5]} -> GrayLevel[0.5], {4, 3,
GrayLevel[0.5]} -> GrayLevel[0.5], {2, 3,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {4, 1,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {4, 4,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {3, 2,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {4, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {3, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {4, 2,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {5, 2,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {2, 1,
GrayLevel[0.5]} -> GrayLevel[0.5], {2, 2,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {2, 3,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {2, 4,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {4, 2,
GrayLevel[0.5]} -> GrayLevel[0.5], {1, 3,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {2, 1,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {1, 1,
GrayLevel[0.5]} -> GrayLevel[0.5], {2, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {1, 2,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {4, 4,
RGBColor[0, 0, 1]} -> RGBColor[0, 0, 1], {5, 3,
RGBColor[1, 0, 0]} -> RGBColor[1, 0, 0], {2, 2,
GrayLevel[0.5]} -> GrayLevel[0.5], {5, 2,
GrayLevel[0.5]} -> GrayLevel[0.5]}}]], First -> Last];
res = N[Total[Table[Boole[SameQ[
FixedPointList[RandomChoice[
Lookup[edgeList, Key[#], {True}]] &,
{5, 2, Red}][[-3]], {5, 3, Red}]], 100000]
]/100000];
res -> Row[{Times[100, Abs@Divide[res - 1/90, Mean[{res, 1/90}]]],
"% difference"
}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/026d883cf3255a60.png) |
| Out[16]= |  |
Use WeightedAdjacencyGraph and DirectedGraphTransferMatrix to answer a Stack Exchange question:
| In[17]:= | ![With[{weights = {{Infinity, 1/2, Infinity, 1/14, 1/14, Infinity, 5/14,
Infinity}, {Infinity, Infinity, 1/9, 1/2, Infinity, 7/18, Infinity, Infinity}, {1/8, 7/16, Infinity, 3/16, 1/8, Infinity, 1/8, Infinity}, {Infinity, 1, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity}, {Infinity, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity}, {Infinity, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity}, {Infinity, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity}, {1, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity, Infinity}}},
Labeled[#, "Result" -> ResourceFunction["DirectedGraphTransferMatrix"][#]] &[
Graph[WeightedAdjacencyGraph[weights],
VertexStyle -> Directive[EdgeForm[Gray], LightGray],
EdgeStyle -> Lighter@Gray,
EdgeLabels -> (x_ :> Framed[Style[Part[weights, Sequence @@ x], Bold, 8],
FrameMargins -> 2, FrameStyle -> Gray,
Background -> Lighter@LightGray]),
GraphLayout -> "LayeredDigraphEmbedding",
ImageSize -> 500
]
]
]](https://www.wolframcloud.com/obj/resourcesystem/images/a46/a46590db-a159-48b6-914b-79358a6e823b/4215c4f4f1e05f49.png) |
| Out[17]= |  |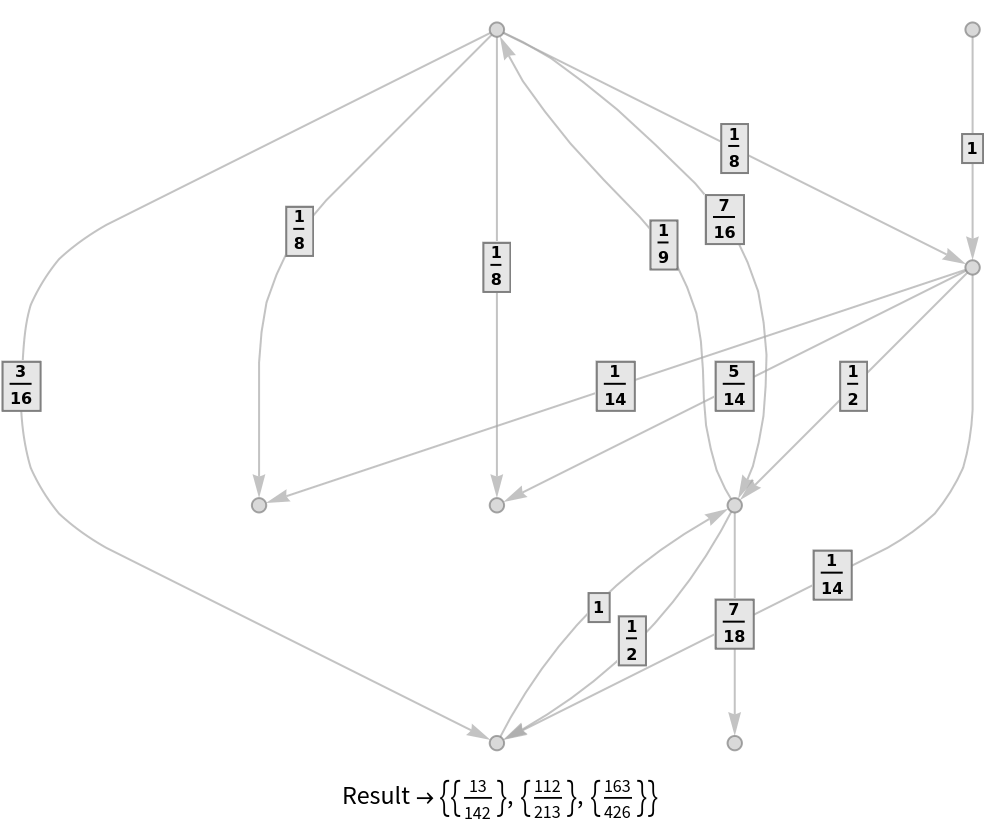
Publisher
Related Links
Version History
- 1.0.0 – 21 August 2023
Source Metadata
Related Resources
Related Symbols
License Information
This work is licensed under a Creative Commons Attribution 4.0 International License