Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DiracMatrix

Source Notebook

Evaluate Dirac matrices in any dimension

Contributed by: Enrique Zeleny

ResourceFunction["DiracMatrix"][n]

gives the nth Dirac matrix.

Details and Options

Dirac matrices for dimensions higher than four can be generalized as Kronecker products of Pauli matrices.
For dimension n, the number of Dirac matrices is the same as n (labeled from 1 to n), and the dimension of the matrices is 2ν×2ν, where n=2ν.

Examples

Basic Examples (2) 

Standard Dirac matrices:

In[1]:=
ResourceFunction["DiracMatrix"][1]
Out[1]=
In[2]:=
ResourceFunction["DiracMatrix"][4]
Out[2]=

Plot matrices:

In[3]:=
ArrayPlot[ResourceFunction["DiracMatrix"][4], ColorFunction -> Hue, ColorRules -> {0 -> White, I -> Red, -I -> Green, 1 -> Blue, -1 -> Yellow}, Mesh -> True]
Out[3]=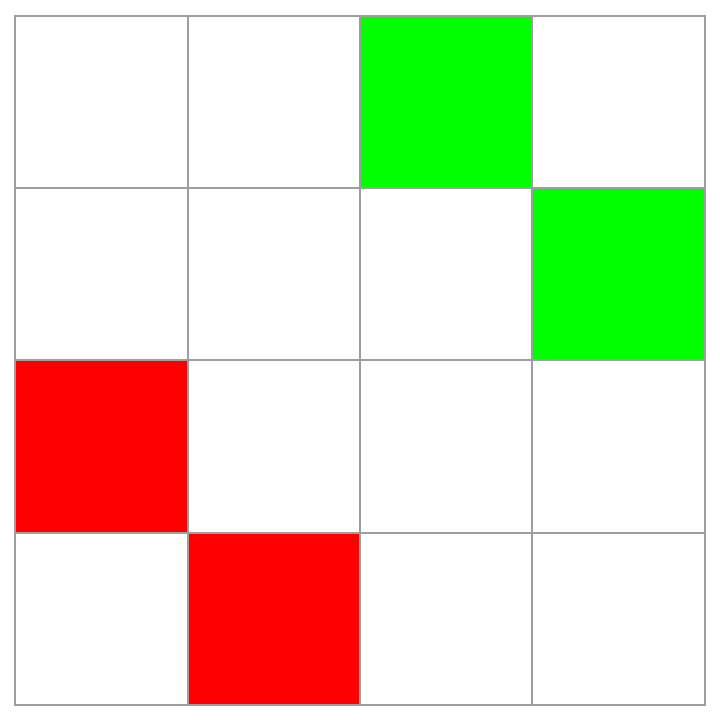

With higher dimensions:

In[4]:=
GraphicsGrid[{Table[ ArrayPlot[ResourceFunction["DiracMatrix"][n, "Dimension" -> 8], ColorFunction -> Hue, ColorRules -> {0 -> White, I -> Red, -I -> Green, 1 -> Blue, -1 -> Yellow}, Mesh -> True], {n, 8}]}, ImageSize -> 650]
Out[4]=

Options

Dimension

In[5]:=
ResourceFunction["DiracMatrix"][1, "Dimension" -> 4]
Out[5]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 2.0.0 – 18 August 2020
  • 1.0.0 – 11 March 2019

Source Metadata

  • Citation:
    • Pais, A. "On Spinors in n Dimensions." Journal of Mathematical Physics, vol. 3, no. 6, 1135–1139, 1962. DOI: 10.1063/1.1703856

Related Resources

License Information