Details
Breadth-first and depth-first searches are two similar methods for brute-force solving problems of combinatorial enumeration.
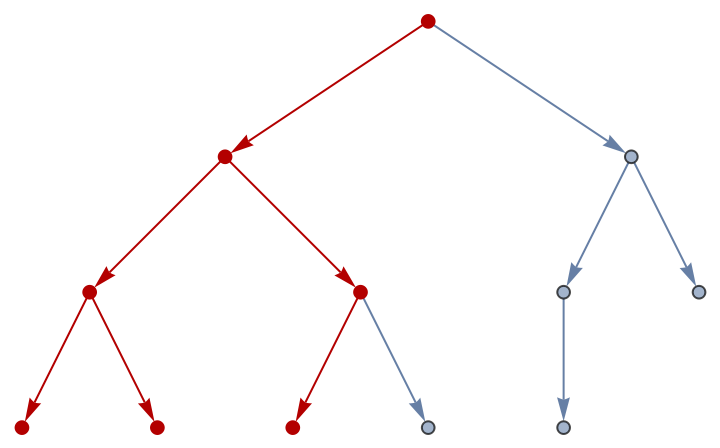
A depth-first search starts at a node, and traverses from child to grandchild downward until either a solution is found, or can be shown not to exist. It will then backtrack up one level, taking the next child at that level and again proceeding downward. Whenever a given level is exhausted of possibilities it goes up a level and over to the next child.
Breadth-first searches in contrast proceed horizontally, visiting all children before going to grandchildren.
This
ResourceFunction["DepthFirstSearch"] may be used effectively when only one valid solution is needed; otherwise, a breadth-first search using something like
NestWhile can often get the desired results in less time. The reason is that depth-first search incurs an extra cost when backtracking, whereas breadth-first search does not need to backtrack.
ResourceFunction["DepthFirstSearch"] includes a usage that operates on directed graphs. This particular usage compares well with the
System function
DepthFirstScan, and can be used to obtain similar outputs (see "Properties and Relations" section below).
When traversing an input graph, the algorithm simply follows directed edges immediately to terminal nodes, backtracks to branch points, and continues to take new paths until a solution is found. In practice, this can be done by keeping a path history as a memory stack.
The two primary methods generate partial search graphs, rather than requiring a complete search graph as input. Generation of a search space is done using a state update function, either stateUpdate or iterator.
Function
stateUpdate takes an input
state as a first argument and draws a second argument from
levelData. The list
levelData is partitioned into sub-lists containing state differentials as items. An input state at level
t is then combined with a differential from the
(t+1)th sub-list of
levelData to obtain the next state. If the input
state is inconsistent with the next differential state from
levelData,
stateUpdate will return
Nothing. This is a failure signal, which causes the algorithm to keep searching for a valid solution. Valid solutions are obtained by combining one differential from each level of
levelData, and they must also satisfy the test
solutionQ.
Similarly, when a state is input to an iterator, the return is a list of candidate states or an empty list. The empty list is a termination condition, which passes the candidate solution to solutionQ. If the state satisfies solutionQ it will be returned as a positive result. If the state does not satisfy solutionQ, it is ignored and the search continues. As opposed to the method using levelData, enumerating the search space via an iterator allows solutions to be found at any depth.
The test solutionQ should be a function of one variable. Either it takes the name of a terminal vertex on an input graph, or it takes a terminal state created via stateUpdate or iterator. In fact, states generated by stateUpdate or iterator can be thought of as nodes on a search graph.
No two backtracking problems are exactly alike, and results can vary based on ordering of candidate states. Optimizations can often be found by including heuristic-based state selection in either stateUpdate or iterator.
![HighlightGraph[KaryTree[12, DirectedEdges -> True], Graph[
ResourceFunction["DepthFirstSearch"][
KaryTree[12, DirectedEdges -> True], 1,
(True &), 3, True]["Edges"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/0dca566a8071e897.png)
![ResourceFunction["DepthFirstSearch"][
Function[MapThread[Append, {#1, #2}] /. {0 -> Nothing}],
{{}, {}}, IdentityMatrix[2] # & /@ Range[7],
SameQ @@ (Total /@ #) &]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/1b49bb36b2658e0a.png)
![ResourceFunction["DepthFirstSearch"][
Function[MapThread[Append, {#1, #2}] /. {0 -> Nothing}],
{{}, {}}, IdentityMatrix[2] # & /@ Range[7],
SameQ @@ (Total /@ #) &, 2]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/6df9cf45b1e08a5f.png)
![ResourceFunction["DepthFirstSearch"][
Function[MapThread[Append, {#1, #2}] /. {0 -> Nothing}],
{{}, {}}, IdentityMatrix[2] # & /@ Range[7],
SameQ @@ (Total /@ #) &, All]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/01724159a4263ae0.png)
![ResourceFunction["DepthFirstSearch"][
Function[{state}, If[SameQ[#, {}], {},
Append[state, #]] & /@ Complement[
VertexOutComponent[
PolyhedronData["Cube", "Skeleton"],
Last[state], {1}], state]], {1},
And[Length[#] == 8, GraphDistance[
PolyhedronData["Cube", "Skeleton"],
First[#], Last[#]] == 1] &]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/052f9b9b4f04c54a.png)
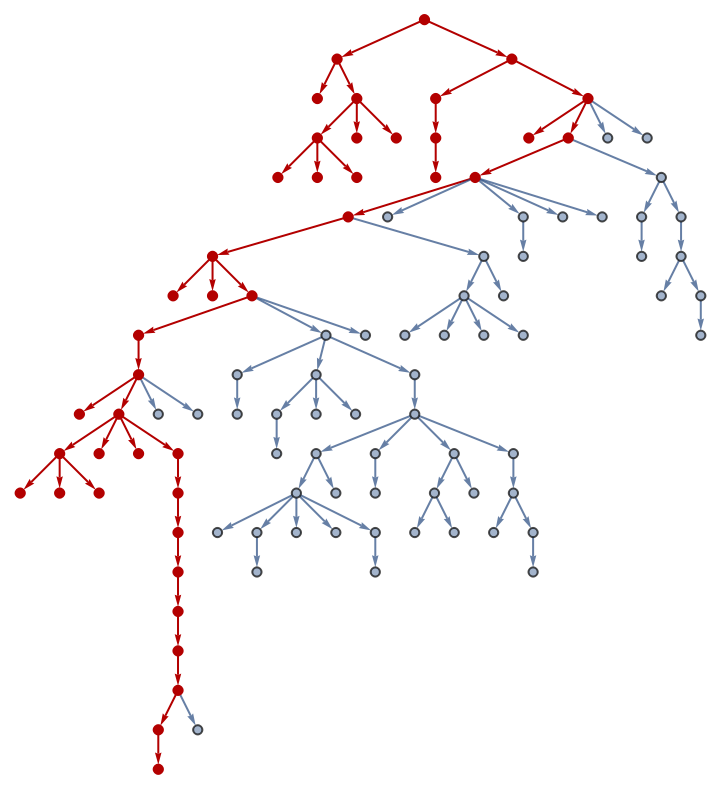
![With[{t0 = (SeedRandom[123324]; RandomTree[100]),
g0 = (SeedRandom[123324]; IndexGraph[
TreeGraph[RandomTree[100]]])},
HighlightGraph[g0,
Graph[ResourceFunction["DepthFirstSearch"][g0, 100,
SameQ[GraphDistance[g0, 100, #],
TreeDepth[t0]] &, 1, True]["Edges"]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/6657e6fdd0524afa.png)
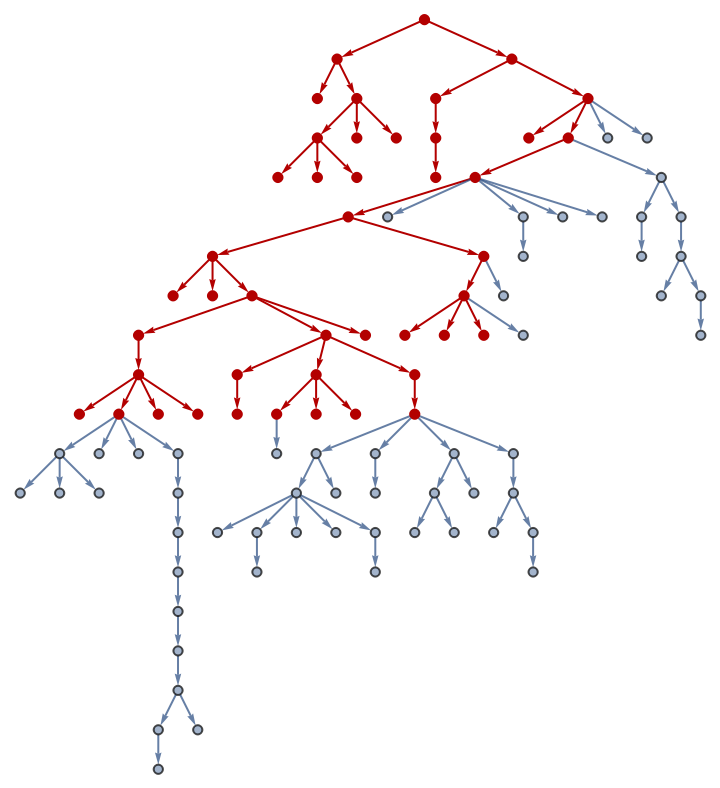
![With[{t0 = (SeedRandom[123324]; RandomTree[100]),
g0 = (SeedRandom[123324]; IndexGraph[
TreeGraph[RandomTree[100]]])},
HighlightGraph[g0,
Graph[ResourceFunction["DepthFirstSearch"][g0, 100,
True &, 20, 10, True]["Edges"]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/211e589715556587.png)
![Module[{g0 = (SeedRandom[123324]; IndexGraph[
TreeGraph[RandomTree[100]],
VertexSize -> Small,
VertexStyle -> Directive[LightGray, EdgeForm[Gray]],
EdgeStyle -> Directive[Thick, Arrowheads[0.025]]]),
leafCount, progress},
leafCount = CountsBy[VertexList[g0], VertexOutDegree[g0, #] &][0];
progress = Map[ResourceFunction["DepthFirstSearch"][g0, 100,
(True &), #, True] &, Range[leafCount]];
HighlightGraph[g0,
MapThread[Style[#1, #2] &,
{Prepend[Complement @@ Reverse[#] & /@ Partition[
#["Edges"] & /@ progress, 2, 1],
progress[[1]]["Edges"]] ,
Darker@Hue[#/(leafCount + 5)
] & /@ Range[leafCount]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/15227433e8392be0.png)

![Module[{g0 = (SeedRandom[123324]; IndexGraph[
TreeGraph[RandomTree[100]],
VertexSize -> Small,
VertexStyle -> Directive[LightGray, EdgeForm[Gray]],
EdgeStyle -> Directive[Thick, Arrowheads[0.025]]]),
leafCount, progress, ind = 1},
leafCount = CountsBy[VertexList[g0],
VertexOutDegree[g0, #] &][0];
progress = Reap[DepthFirstScan[g0, 100,
{"PrevisitVertex" -> ((Sow[# -> ind++]) &)}]][[2, 1]];
HighlightGraph[g0, Reverse@MapThread[
Style[DirectedEdge @@@ Partition[#1, 2, 1], #2] &,
{FindShortestPath[g0, 100, #] & /@ SortBy[Select[
VertexList[g0], VertexOutDegree[g0, #] == 0 &], # /. progress &] ,
Darker@Hue[#/(leafCount + 5)
] & /@ Range[leafCount]}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/4394d12496f5ef03.png)

![ResourceFunction["DepthFirstSearch"][
Function[With[{tot = #1[[2]] + #2},
If[tot <= 10,
Append[#1[[1]], #2] -> tot,
Nothing]]], {} -> 0,
ConstantArray[Range[8], 3],
Last[#] == 10 &, All]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/2eaffea2e01d96d6.png)

![ResourceFunction["DepthFirstSearch"][
Function[{state}, With[{
tot = Total[state[[1]]],
len = Length[state[[1]]]},
If[len == 3, {},
Map[Append[state[[1]], #] -> (state[[2]] + #) &,
Range[1, (10 - tot) - (3 - (len + 1))]]]]],
{} -> 0,
Last[#] == 10 &, All]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/452ca0dd3b228f03.png)

![With[{
e1 = ResourceFunction["DepthFirstSearch"][
Function[With[{tot = #1[[2]] + #2},
If[tot <= 10,
Append[#1[[1]], #2] -> tot,
Nothing]]],
{} -> 0,
ConstantArray[Range[8], 3],
Last[#] == 10 &, All, True]["Edges"],
e2 = ResourceFunction["DepthFirstSearch"][
Function[{state}, With[{
tot = Total[state[[1]]],
len = Length[state[[1]]]},
If[len == 3, {},
Map[Append[state[[1]], #] -> (state[[2]] + #) &,
Range[1, (10 - tot) - (3 - (len + 1))]]]]],
{} -> 0,
Last[#] == 10 &, All, True]["Edges"]},
And[UnsameQ[e1, e2],
SubsetQ[e1, e2]]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/388c45f496862a4f.png)
![TimeConstrained[
ResourceFunction["DepthFirstSearch"][CycleGraph[4], 1,
True &, All], 5]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/55501d1f465944d7.png)
![TimeConstrained[
ResourceFunction["DepthFirstSearch"][Function[{n},
If[IntegerQ[n], {n/2, 3 n + 1}, {}]],
1, True &, All], 5]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/5c545f1a20a57711.png)
![Grid[Partition[
Graph[ResourceFunction["DepthFirstSearch"][
Function[{n}, If[IntegerQ[n], {n/2, 3 n + 1}, {}]],
1, True &, All, #, True]["Edges"],
ImageSize -> 120] & /@ Range[12], 4],
Spacings -> {2, 2}, Frame -> All,
FrameStyle -> LightGray]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/558d30c4db06b0ab.png)

![With[{g1 = (SeedRandom[2414323];
Graph[ResourceFunction["ToDirectedAcyclicGraph"
][#, VertexList[#][[{1, 2}]]],
VertexCoordinates -> Automatic,
GraphLayout -> "LayeredDigraphEmbedding",
AspectRatio -> 2/3] &[
WeaklyConnectedGraphComponents[
RandomGraph[{300, 350}]][[1]]])},
HighlightGraph[g1, {
Style[Complement[#[[1]], #[[2]]], Blue],
Style[Complement[#[[2]], #[[1]]], Darker@Green],
Style[Intersection[#[[2]], #[[1]]], Blend[{Blue, Green}]]}] &@(
ResourceFunction["DepthFirstSearch"][g1, #, True &, All, True][
"Edges"] & /@ {1, 23})]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/31b237fa28fb7994.png)
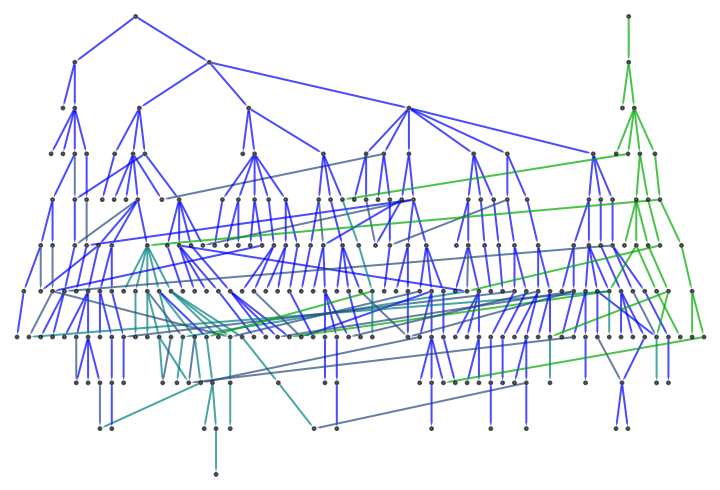
![With[{periodicTemplates = {{{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}, {{1, 1, 0}, {0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}, {1, 1, 0}}, {{0, 1, 1}, {1, 1, 1}, {1, 0, 1}}, {{1, 1, 1}, {1, 1, 0}, {0, 1, 1}}}, templateExpand = Function[{template, size},
With[{colLen = Part[size, 2] + Part[
Dimensions[template], 2] - 1},
Catenate[
Outer[
Function[{row, col},
Part[
RotateRight[
Map[RotateRight[#, col]& ,
Join[
Map[PadRight[#, colLen,
Blank[]]& , template],
Table[
ConstantArray[
Blank[], colLen], {Part[size, 1] - 1}]]], row],
Span[-Part[size, 1], -1],
Span[-Part[size, 2], -1]]],
Range[0, Part[size, 1] + Part[
Dimensions[template], 1] - 2],
Range[0, Part[size, 2] + Part[
Dimensions[template], 2] - 2], 1]]]],
rowsCombine = Function[{r1, r2},
Catch[
MapThread[
Function[{x, y},
Switch[{x, y}, {
Verbatim[
Blank[]],
Blank[]}, y, {
Blank[],
Verbatim[
Blank[]]}, x, {
Blank[],
Blank[]},
If[x === y, x,
Throw[Nothing]]]], {r1, r2}]]], size = 10},
Labeled[ArrayPlot[Partition[
ResourceFunction["DepthFirstSearch"][rowsCombine, ConstantArray[_, size^2], Reverse[Union[#]
] & /@ Transpose[(Catenate /@ templateExpand[#, {size, size}]
) & /@ periodicTemplates], True &], size]],
Row[ArrayPlot[#, ImageSize -> 40] & /@ periodicTemplates,
Spacer[5]], Spacings -> {1, 1}]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/7c7a7dd98bc65ad7.png)

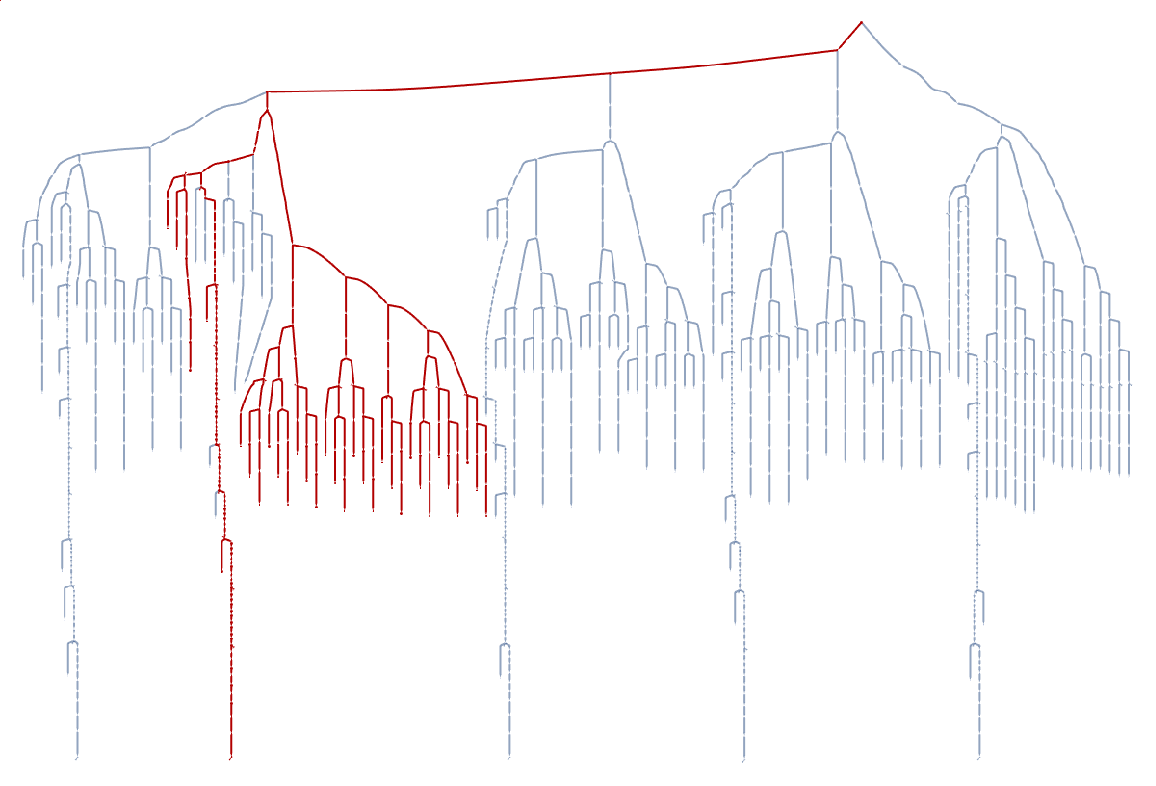
![Module[{periodicTemplates = {{{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}, {{1, 1, 0}, {0, 1, 1}, {1, 1, 1}}, {{1, 0, 1}, {1, 1, 1}, {1, 1, 0}}, {{
0, 1, 1}, {1, 1, 1}, {1, 0, 1}}, {{1, 1, 1}, {1, 1, 0}, {0, 1, 1}}}, templateExpand = Function[{template, size},
With[{colLen = Part[size, 2] + Part[
Dimensions[template], 2] - 1},
Catenate[
Outer[
Function[{row, col},
Part[
RotateRight[
Map[RotateRight[#, col]& ,
Join[
Map[PadRight[#, colLen,
Blank[]]& , template],
Table[
ConstantArray[
Blank[], colLen], {Part[size, 1] - 1}]]], row],
Span[-Part[size, 1], -1],
Span[-Part[size, 2], -1]]],
Range[0, Part[size, 1] + Part[
Dimensions[template], 1] - 2],
Range[0, Part[size, 2] + Part[
Dimensions[template], 2] - 2], 1]]]],
rowsCombine = Function[{r1, r2},
Catch[
MapThread[
Function[{x, y},
Switch[{x, y}, {
Verbatim[
Blank[]],
Blank[]}, y, {
Blank[],
Verbatim[
Blank[]]}, x, {
Blank[],
Blank[]},
If[x === y, x,
Throw[Nothing]]]], {r1, r2}]]], size = 10, init, levelData},
init = ConstantArray[_, size^2];
levelData = Reverse[Union[#]] & /@ Transpose[
(Catenate /@ templateExpand[#, {size, size}]
) & /@ periodicTemplates];
With[{
g1 = Graph[ResourceFunction["DepthFirstSearch"][
rowsCombine, init, levelData,
True &, All, True]["Edges"],
GraphLayout -> "LayeredDigraphEmbedding",
ImageSize -> 600, AspectRatio -> 2/3, VertexSize -> 1/4],
g2 = Graph[ResourceFunction["DepthFirstSearch"][rowsCombine,
init, levelData,
True &, 1, True]["Edges"]]
}, HighlightGraph[
VertexReplace[g1, vert_ :> (vert /. {Verbatim[_] -> x})],
VertexReplace[g2, vert_ :> (vert /. {Verbatim[_] -> x})]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/58e824baa0b4a040.png)
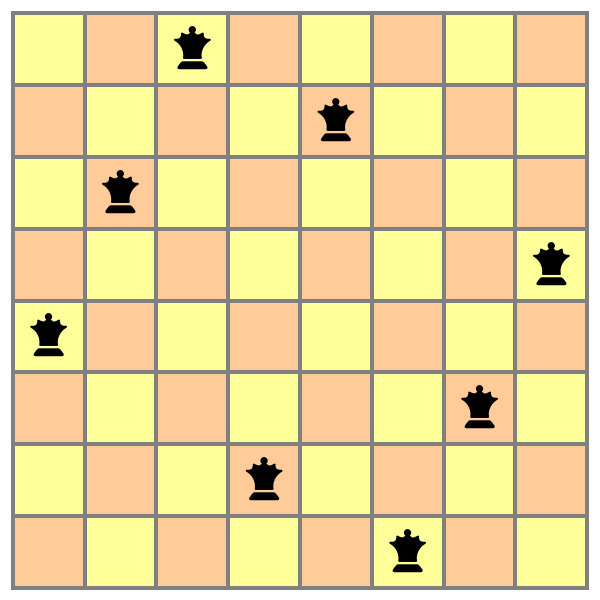
![With[{rowsCombine = Function[{r1, r2},
Catch[
MapThread[
Function[{x, y},
Switch[{x, y}, {
Verbatim[
Blank[]],
Blank[]}, y, {
Blank[],
Verbatim[
Blank[]]}, x, {
Blank[],
Blank[]},
If[x === y, x,
Throw[Nothing]]]], {r1, r2}]]],
queenCoversData = Function[{size},
Table[
Flatten[
ReplacePart[
Table[
If[
Or[i == k, j == l, i + j == k + l, i - j == k - l], 0,
Blank[]], {i,
Part[size, 1]}, {j,
Part[size, 2]}], {k, l} -> 1]], {k,
Part[size, 1]}, {l,
Part[size, 2]}]],
queensDepict = ResourceFunction["CharacterArrayPlot"][
2 Partition[#, 8] + Table[
Mod[i + j, 2], {i, 8}, {j, 8}], ColorRules -> {Pattern[x,
Blank[]] :> <|0 -> Lighter[Yellow, 0.6], 1 -> Lighter[Orange, 0.6]|>[
Mod[x, 2]]}, "CharacterRules" -> {1 -> "", 0 -> "", Pattern[x,
Blank[]] :> FromCharacterCode[9819]}, "CharacterStyleRules" -> {Pattern[x,
Blank[]] :> {20, Black}}, MeshStyle -> Directive[Gray, Thick], ImageSize -> 300]& },
queensDepict[
ResourceFunction["DepthFirstSearch"][
rowsCombine,
ConstantArray[_, 64],
queenCoversData[{8, 8}],
SameQ[Partition[#, 8],
Reverse /@ Reverse[Partition[#, 8]]] &]]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/082fd227b5bfde02.png)
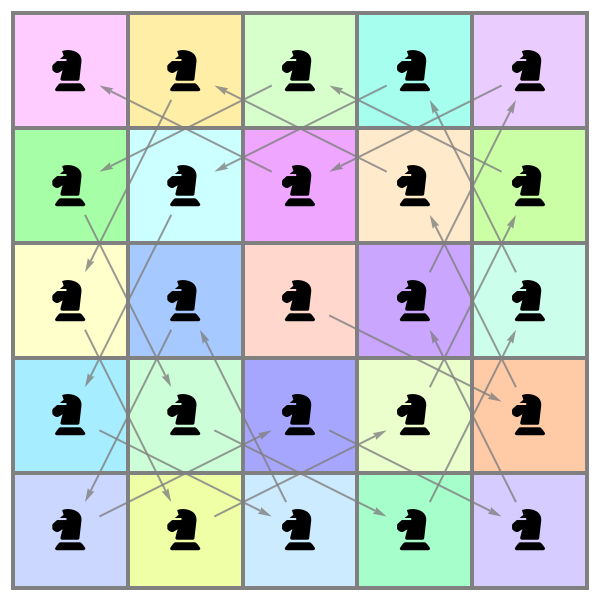
![With[{moves = {{-2, -1}, {-2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {2, -1}, {2, 1}}, iterateWalk = Function[{board, moves},
With[{max = Max[board], pos = Part[
Position[board,
Max[board]], 1]},
Map[ReplacePart[board, # -> max + 1]& ,
Select[
Map[pos + #& ,
RandomSample[moves]], If[
Apply[And,
Thread[
Inequality[
Dimensions[board], GreaterEqual, #, Greater, {0, 0}]]], Part[board,
Apply[Sequence, #]] == 0, False]& ]]]],
knightsDepict = Show[{
(ResourceFunction["CharacterArrayPlot"][#, ColorRules -> {Pattern[x,
Blank[]] :> (If[Mod[x, 2] == 0,
Lighter[#, 0.65],
Lighter[#, 0.8]]& )[
Hue[x/30]]}, "CharacterRules" -> {Pattern[x,
Blank[]] :> ""}, MeshStyle -> Directive[Gray, Thick], ImageSize -> 300]& )[#],
Function[{sol},
(Graph[
EdgeList[#], VertexShape -> Style[
FromCharacterCode[9822], Black, 20], VertexCoordinates -> Map[# -> Reverse[{-1, 1} #]& ,
VertexList[#]], VertexSize -> 1/2, PerformanceGoal -> "Quality", EdgeStyle -> Directive[
Opacity[0.8, Gray]]]& )[
PathGraph[
Map[Part[
Position[sol, #], 1]& ,
Range[25]], DirectedEdges -> True]]][#]}]& },
knightsDepict@ResourceFunction["DepthFirstSearch"][
Function[iterateWalk[#, moves]],
ReplacePart[ConstantArray[0, {5, 5}], {3, 3} -> 1],
Max[#] == 25 &, 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/697aeaab057498cb.png)
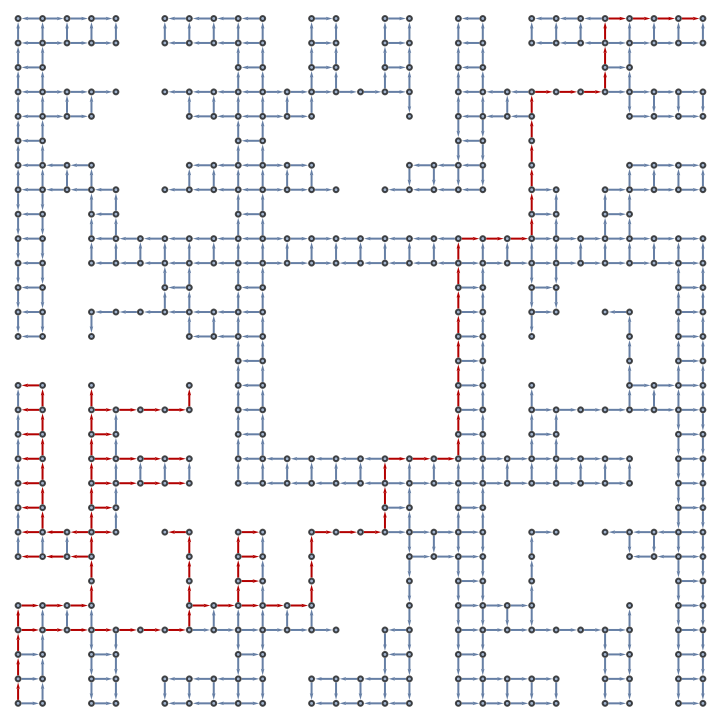
![With[{g1 = (SeedRandom["mazeTest"]; ResourceFunction["ToDirectedAcyclicGraph"][
ResourceFunction["RandomSierpinskiMaze"][2, AdjacencyGraph], {{1, 1}}])},
Graph[HighlightGraph[g1, ResourceFunction["DepthFirstSearch"][g1, {1, 1}, SameQ @@ # &, True]["Edges"]
], VertexCoordinates -> (# -> # & /@ VertexList[g1])]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/4609b123d06964e7.png)
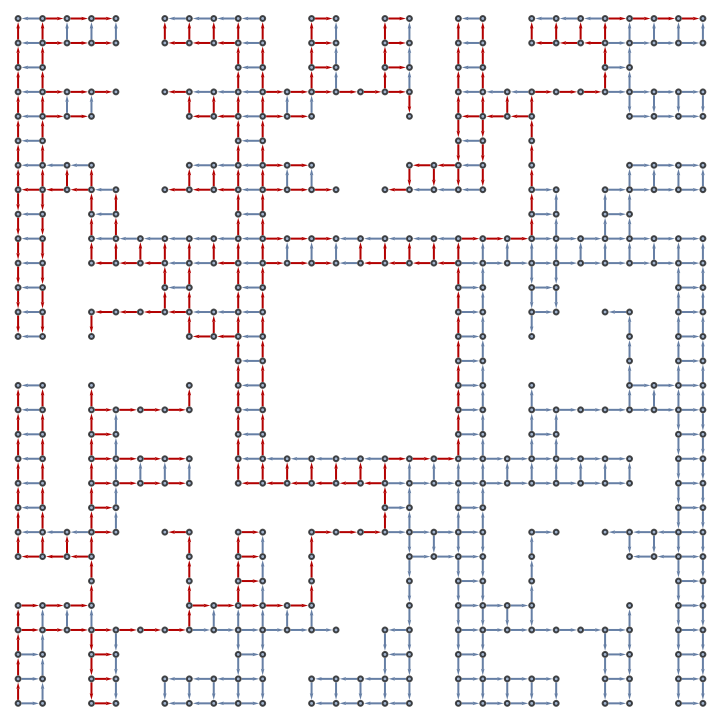
![With[{g1 = (SeedRandom["mazeTest"];
ResourceFunction["ToDirectedAcyclicGraph"][
ResourceFunction["RandomSierpinskiMaze"][
2, AdjacencyGraph], {{1, 1}}])},
Graph[HighlightGraph[g1, ResourceFunction["DepthFirstSearch"][
Association[# -> SortBy[
Cases[EdgeList[g1], DirectedEdge[#, x_] :> x],
{-#[[2]], -#[[1]]} &] & /@ Sort[VertexList[g1]]],
{1, 1}, SameQ @@ # &, True]["Edges"]],
VertexCoordinates -> (# -> # & /@ VertexList[g1])]]](https://www.wolframcloud.com/obj/resourcesystem/images/daf/dafc3461-daa1-42b3-9472-549fe8e14852/5212e8e4ce78426e.png)