Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Convert a Hermitian-definite matrix pencil into a matrix with the same eigenvalues
ResourceFunction["DefinitePencilReduce"][{m,a}] yields a list of matrices {s,t}, where s is a Hermitian matrix with the same eigenvalues as the Hermitian definite matrix pencil {m,a}, and t is a transformation matrix that transforms the eigenvectors of s into the eigenvectors of {m,a}. |
A symmetric definite pencil:
| In[1]:= |
Reduce the pencil:
| In[2]:= |
| Out[2]= |
Compute the eigenvalues of the transformed matrix:
| In[3]:= |
| Out[3]= | 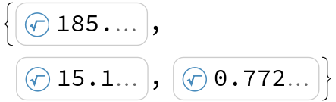 |
These are the same as the eigenvalues of the original pencil:
| In[4]:= |
| Out[4]= | 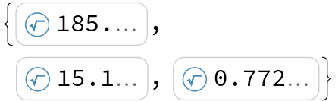 |
Compute the normalized eigenvectors of the transformed matrix:
| In[5]:= |
| Out[5]= |  |
These are the same as the eigenvectors of the original pencil, up to a normalization constant:
| In[6]:= |
| Out[6]= |  |
A machine precision symmetric definite pencil:
| In[7]:= |
Reduce the pencil:
| In[8]:= |
| Out[8]= |
Compute the eigenvalues of the transformed matrix:
| In[9]:= |
| Out[9]= |
These are the same as the eigenvalues of the original pencil:
| In[10]:= |
| Out[10]= |
Compute the normalized eigenvectors of the transformed matrix:
| In[11]:= |
| Out[11]= |
These are the same as the eigenvectors of the original pencil, up to a normalization constant:
| In[12]:= |
| Out[12]= |
Reduce an exact symmetric definite pencil:
| In[13]:= | ![MatrixForm /@ ResourceFunction["DefinitePencilReduce"][{( {
{2, 3, 4},
{3, 1, 2},
{4, 2, 3}
} ), ( {
{3, 1, 1},
{1, 3, -1},
{1, -1, 3}
} )}]](https://www.wolframcloud.com/obj/resourcesystem/images/ed1/ed1403ce-d35c-487b-b79f-4a9425e57e5a/5409fcf6dc884797.png) |
| Out[13]= | 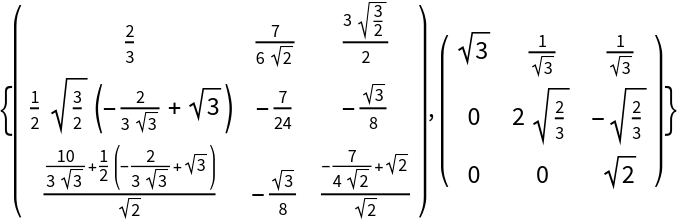 |
Reduce a symmetric definite pencil with 24-digit precision arithmetic::
| In[14]:= | ![ResourceFunction["DefinitePencilReduce"][N[{( {
{2, 3, 4},
{3, 1, 2},
{4, 2, 3}
} ), ( {
{3, 1, 1},
{1, 3, -1},
{1, -1, 3}
} )}, 24]]](https://www.wolframcloud.com/obj/resourcesystem/images/ed1/ed1403ce-d35c-487b-b79f-4a9425e57e5a/3cc85612335d0723.png) |
| Out[14]= |  |
A random symmetric definite pencil:
| In[15]:= |
| Out[15]= |  |
Reduce the pencil:
| In[16]:= |
| Out[16]= |  |
A random Hermitian definite pencil:
| In[17]:= |
| Out[17]= |  |
Reduce the pencil:
| In[18]:= |
| Out[18]= |  |
Use the "Cholesky" method to reduce the definite pencil:
| In[19]:= |
| Out[19]= |
Use the "Eigensystem" method to reduce the definite pencil:
| In[20]:= |
| Out[20]= |
A definite pencil:
| In[21]:= | ![{m, a} = N[{( {
{2, 3, 4},
{3, 1, 2},
{4, 2, 3}
} ), ( {
{3, 1, 1},
{1, 3, -1},
{1, -1, 3}
} )}];](https://www.wolframcloud.com/obj/resourcesystem/images/ed1/ed1403ce-d35c-487b-b79f-4a9425e57e5a/41b6d39cb4ef9e13.png) |
Reduce the definite pencil:
| In[22]:= |
| Out[22]= |
Verify that m is given by ConjugateTranspose[t].s.t:
| In[23]:= |
| Out[23]= |
Verify that a is given by ConjugateTranspose[t].t:
| In[24]:= |
| Out[24]= |
DefinitePencilReduce is left unevaluated if the argument is not a definite pencil:
| In[25]:= | ![ResourceFunction["DefinitePencilReduce"][{( {
{2, 3, 4},
{3, 1, 2},
{4, 2, 3}
} ), ( {
{1, 1, 1},
{1, 1, -1},
{1, -1, 1}
} )}]](https://www.wolframcloud.com/obj/resourcesystem/images/ed1/ed1403ce-d35c-487b-b79f-4a9425e57e5a/60a0edf76b306ea6.png) |
| Out[25]= |
| In[26]:= | ![PositiveDefiniteMatrixQ[( {
{1, 1, 1},
{1, 1, -1},
{1, -1, 1}
} )]](https://www.wolframcloud.com/obj/resourcesystem/images/ed1/ed1403ce-d35c-487b-b79f-4a9425e57e5a/1ac27fd0964248a1.png) |
| Out[26]= |
This work is licensed under a Creative Commons Attribution 4.0 International License