Author Notes
In general, the
Precision of an approximate real number is the effective number of decimal digits in it which are treated as significant for computations. In contrast to the other types of approximate numbers (the arbitrary‐precision numbers), machine numbers contain a fixed number of digits (
MachinePrecision). Since they maintain no information on their precision, all their digits are treated as significant during computations.
In rare occasions one wants to prescribe the effective number of digits in a machine number, putting zeros into the trail and perhaps modifying the last significant digit. In everyday life, this operation is called rounding, but the Wolfram Language function
Round is not designed specifically for machine numbers. It is not straightforward to use
Round to set explicitly the number of significant digits in the decimal representation of a machine number.
The resource function DecimalRound takes a machine number and the number of required digits and attempts to provide the result as a machine number with exactly the requested number of significant digits.
In the following example, numlist consists of five numbers, originally having wildly spread precisions. For instance, the first number is the AvogadroConstant in SI which is perfectly defined by an international standard. On the other hand, the fourth number is the result of a calculation to approximate π via dividing 22 by 7 and the indicated precision is itself the result of an approximate calculation. Here is the list:
When we create the list of machine numbers, we lose some information on precision (for instance our approximate π will look like a 16-digit good approximation), but computations and storage will be more efficient in the world of machine numbers:
Interestingly, some information is preserved, for instance the Avogadro number will still show that it has nine "good" digits, albeit only implicitly, by the fact that seven trailing digits are zeros. If we want to convey our knowledge regarding the approximate π, we should round it to, say, three digits, as we would do it in a hand calculation. DecimalRound can do this.
To be more general, in this example we create a variable which contains possible requirements for the number of significant digits:
Then DecimalRound is called with various combinations of the two arguments:
In the output the column heading shows the rounded machine numbers. The row heading shows the requested digit counts. We use
FullForm to see what we are really having in the result matrix:
Since the function is
Listable, we can easily get a whole row of the matrix as well as as a whole column:
![SeedRandom[1234];
mat = RandomVariate[StableDistribution[0.2], {5, 5}];
invmat = Inverse[mat];
prod = invmat . mat;
normprod = Norm[prod];](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/42845729b1e79e19.png)
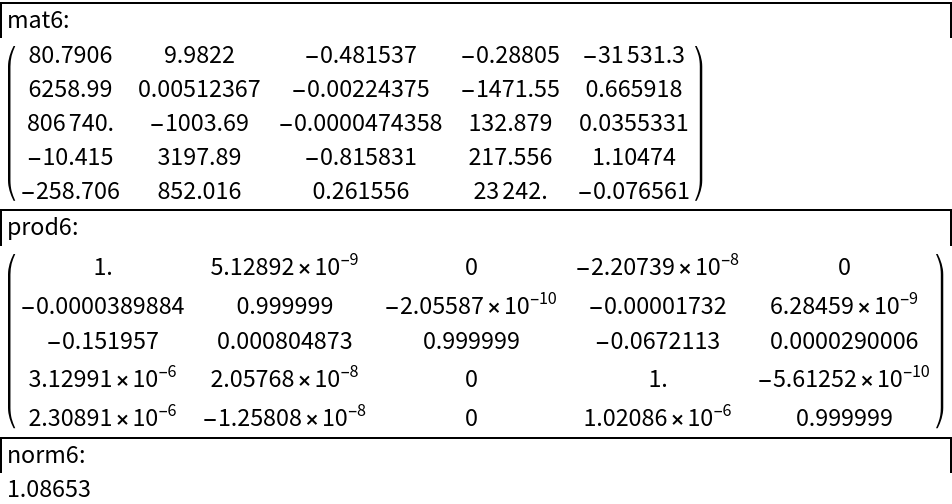
![mat6 = ResourceFunction["DecimalRound"][ mat ];
invmat6 = Inverse[mat6];
prod6 = invmat6 . mat;
normprod6 = Norm[prod6];](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/66404b0285095eed.png)
![Column[{
"mat:",
mat // MatrixForm,
"prod:",
prod // MatrixForm // Chop,
"norm:",
normprod}, Frame -> {{True, None}}]](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/0e84c5f9ac174f74.png)

![Column[{
"mat6:",
mat6 // MatrixForm,
"prod6:",
prod6 // MatrixForm // Chop,
"norm6:",
normprod6}, Frame -> {{True, None}}]](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/52df827544ad3e3c.png)
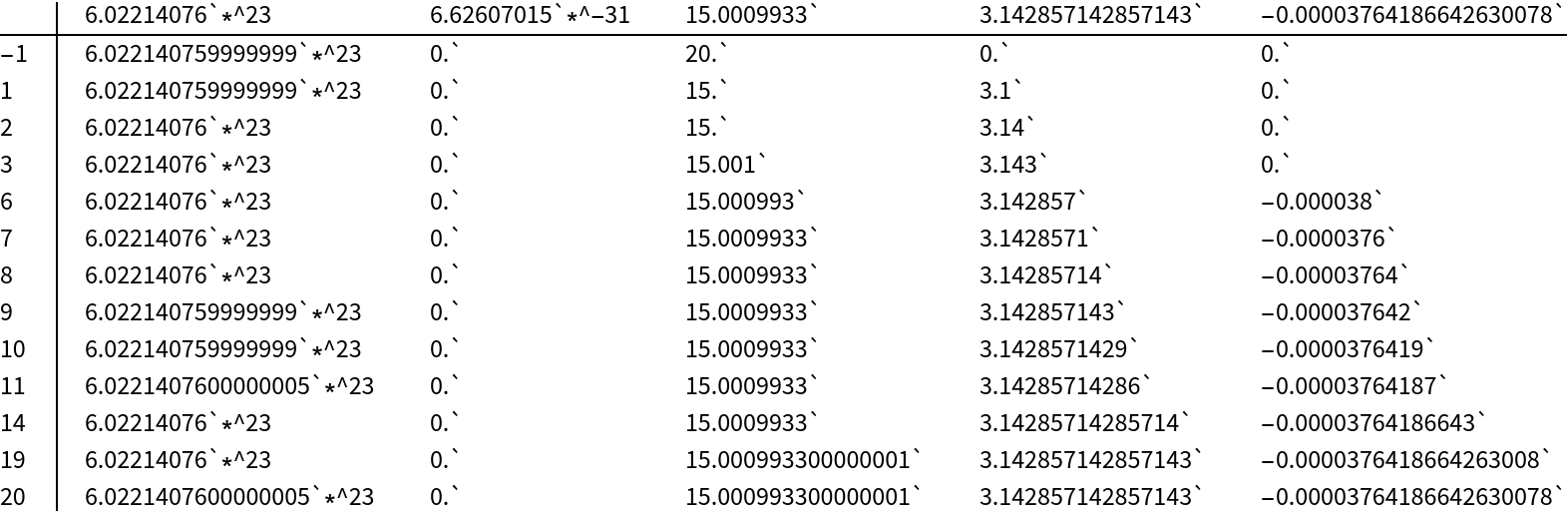
![numlist = {602214076000000000000000, Rational[132521403, 200000000000000000000000000000000000000], 15.0009933`, SetPrecision[22/7., 5.283185307179586], -0.000037641866426300784330078433`25.17567114925435};
machnumlist = N[numlist];
ndiglist = {-1, 1, 2, 3, 6, 7, 8, 9, 10, 11, 14, 19, 20};](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/217227d628595916.png)
![roundedmatrix1 = Table[
Table[Round[machnum, 10^-ndig], {machnum, machnumlist}]
, {ndig, ndiglist}];
TableForm[Map[FullForm, roundedmatrix1, {2}], TableHeadings -> {ndiglist, Map[FullForm, machnumlist]}]](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/0b82fdd07c91ca0e.png)

![roundedmatrix2 = Table[
Table[Round[machnum, 10^-ndig] // N, {machnum, machnumlist}]
, {ndig, ndiglist}];](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/172794d879ae139a.png)
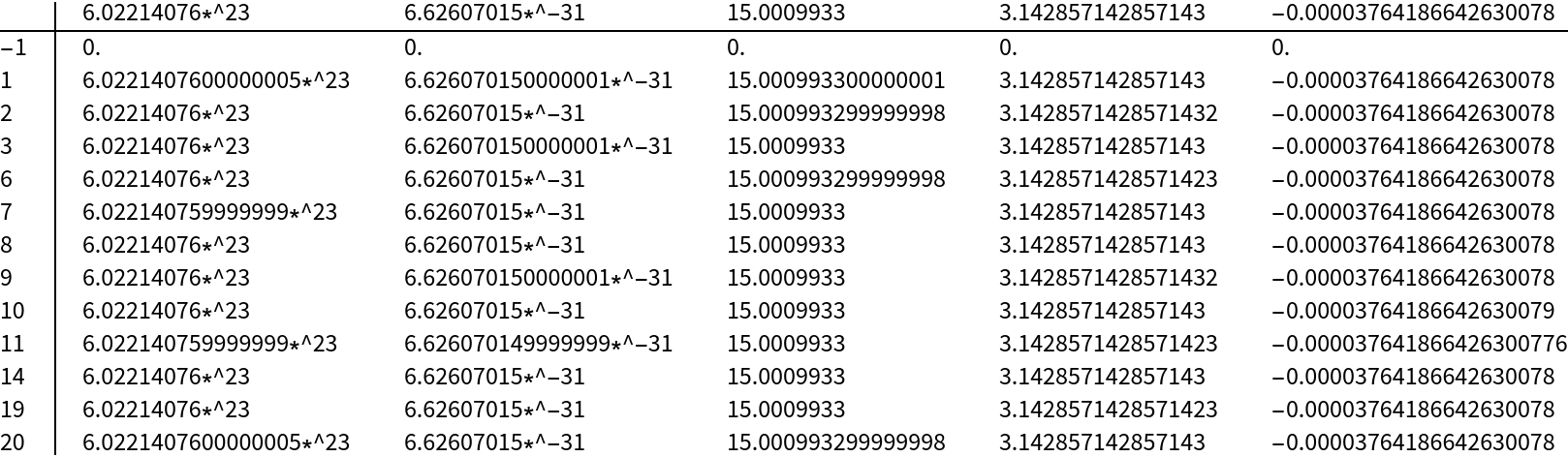
![roundedmatrix3 = Table[
Table[
Round[machnum, Abs[machnum] 10^-ndig] // N, {machnum, machnumlist}]
, {ndig, ndiglist}];](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/4dbc866bf8662680.png)
![DecimalRoundAlt[machnum_, ndig_] := Module[{n, e, nmad, nman, ma, nd},
nd = Clip[Round[ndig], {1, 15}];
n = 20;
{nmad, e} = RealDigits[Abs[machnum]];
nmad = PadRight[nmad, n];
ma = 0 nmad;
ma[[n]] = nman = FromDigits[nmad];
While[n > 1,
nman = FromDigits[Most[nmad]];
If[Last[nmad] >= 5, nman++];
nmad = IntegerDigits[nman];
ma[[--n]] = nman;
If[n == nd, Break[]]
];
N[Sign[machnum] ma[[nd]] 10^(e - nd)] ];](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/7bf4a04da616ab65.png)
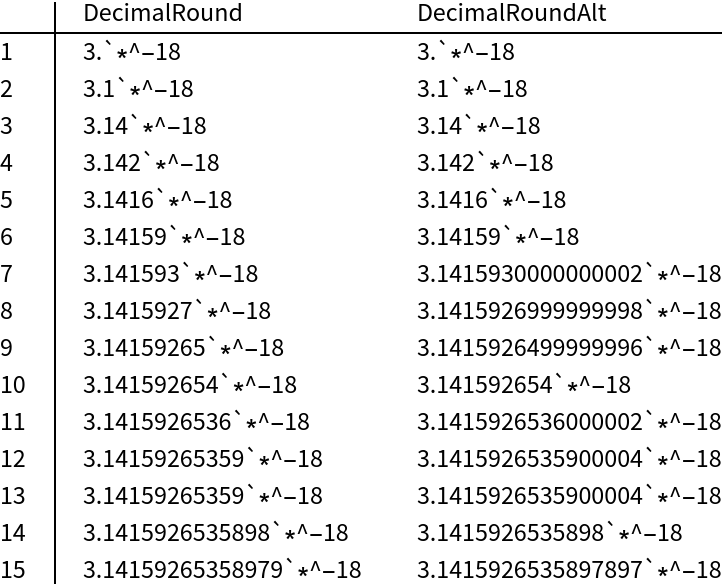
![TableForm[
Table[{ResourceFunction["DecimalRound"][N[Pi 10^-18], n] // FullForm,
DecimalRoundAlt[N[Pi 10^-18], n] // FullForm}, {n, 15}], TableHeadings -> {Range[20], {"DecimalRound", "DecimalRoundAlt"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/366/3662c7df-2571-4780-a6ea-a405621a52c7/4a7606a395e712cf.png)