Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get the decile values of a list of data
ResourceFunction["Decile"][data] gives the 0th to the 10th decile value of data as an assocation. | |
ResourceFunction["Decile"][data,n] gives the nth decile value of data. | |
ResourceFunction["Decile"][data,{n1,n2,n3,…}] gives an Association of the nith decile values of data. |
Find the decile values of some data:
| In[1]:= |
| Out[1]= |
Find the 7th decile:
| In[2]:= |
| Out[2]= |
Find the 1st and 9th decile:
| In[3]:= |
| Out[3]= |
The second argument does not have to be an integer, and can be used to reproduce the interquartile range (IQR):
| In[4]:= | ![d = RandomReal[{0, 1}, 1000];
{ResourceFunction["Decile"][d, 7.5] - ResourceFunction["Decile"][d, 2.5], InterquartileRange[d, {{0, 0}, {1, 0}}]}](https://www.wolframcloud.com/obj/resourcesystem/images/0c7/0c7813f7-ea62-4c38-889a-1c54cec6dedd/55ecfd59133a02f6.png) |
| Out[5]= |
Compute the decile mean of some data:
| In[6]:= |
| Out[7]= |
Get a quick idea of the deciles of a list of numbers (e.g. shoe sizes):
| In[8]:= |
| Out[9]= | 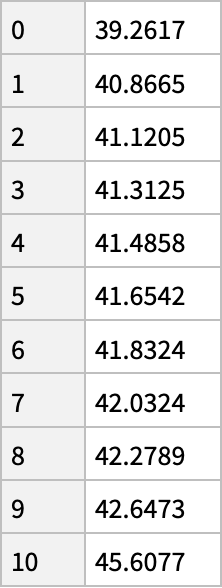 |
| In[10]:= |
The 5th decile is related to Median and Quantile:
| In[11]:= |
| Out[11]= |
The 0th decile is related to the minimum value:
| In[12]:= |
| Out[12]= |
The 10th decile is related to the maximum value:
| In[13]:= |
| Out[13]= |
The second argument has to be non-negative:
| In[14]:= |
| Out[15]= |
The second argument must be equal or less than 10:
| In[16]:= |
| Out[17]= |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License