Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DeBruijnNewmanH

Source Notebook

Compute the values of the function from which the de Bruijn–Newman constant is defined

Contributed by: Riccardo Gatti

ResourceFunction["DeBruijnNewmanH"][z]

computes the value H0(z) where H is the function from which the de Bruijn–Newman constant Λ is defined.

Details and Options

For and , the function is defined as follows: where is the super-exponentially decaying function.
Hλ(z) is symmetrical with respect of z=0, hence Hλ(-z)=Hλ(z).
H0(z) is related to the RiemannXi function via the identity , where . Hence and from definition .

Examples

Basic Examples (3) 

Compute the value of H0(2+5ⅈ):

In[1]:=
ResourceFunction["DeBruijnNewmanH"][2 + I 5]
Out[1]=

Plot of the real part of the complex function H0(x+100ⅈ):

In[2]:=
Plot[Re[ResourceFunction["DeBruijnNewmanH"][x + I 100]], {x, 0, 50}]
Out[2]=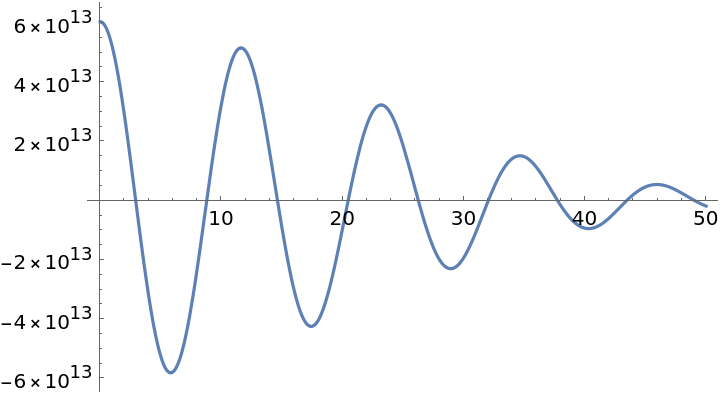

Calculate the value of H0(z) using both an integral definition and the relation with Riemann ζ function. As WorkingPrecision gets larger, the difference between two definitions approaches 0 and the computation could take a few minutes:

In[3]:=
ResourceFunction["DeBruijnNewmanH"][17 + I Sqrt[12], Method -> "Integral", WorkingPrecision -> 5] - N[ResourceFunction["DeBruijnNewmanH"][17 + I Sqrt[12], Method -> "RiemannFunction"]]
Out[3]=

Scope (1) 

If the Riemann hypothesis is correct, then all zeros of H0(z) are real. We check for a specific zero z around 20 that :

In[4]:=
FindRoot[ResourceFunction["DeBruijnNewmanH"][z], {z, 20}, WorkingPrecision -> 30]
Out[4]=

Publisher

Riccardo Gatti

Version History

  • 1.0.0 – 20 January 2021

License Information