Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DataPipeline

Source Notebook

Represent data processing operations as edges and vertices in a graph

Contributed by: Sjoerd Smit

ResourceFunction["DataPipeline"][{operator1,operator2,…}]

represents a linear data processing pipeline of operations.

ResourceFunction["DataPipeline"][{key1→operator1,key2→operator2},{keyi→keyj,…}]

represents a computational network of operations to be applied to data with named vertices keyi.

Details and Options

A data pipeline is a sequence of operations that transforms data. The result of each operation is tested for validity and if any intermediate result is invalid, ResourceFunction["DataPipeline"] bails out and throws an error. In its simplest form, ResourceFunction["DataPipeline"] is a sequence of operations like NetChain, but it can also be used to implement a computational network of operations like in NetGraph. Unlike NetChain and NetGraph, ResourceFunction["DataPipeline"] works with general WL expressions.
All keys in a computational network must be strings.
ResourceFunction["DataPipeline"] takes the following options:
"FailureDetection"Automatichow to determine if a result represents a failure
"CatchMessages"Truewhether to abort if a message is generated
Any expression for which FailureQ is True will always be considered a failure for the whole pipeline and will returned to the top level, regardless of the setting of the "FailureDetection" option.
The default value "FailureDetection"→Automatic also aborts the pipeline if an operation returns Missing[…], Indeterminate, Undefined, $Canceled, $Aborted or a type of infinity. Setting "FailureDetection"→None will not consider these values as failure modes. You can also specify your own test function "FailureDetection"→fun, which uses fun to determine if a result represents a failure or not. If the specified function fun returns True, for any input, intermediate result or final result, the ResourceFunction["DataPipeline"] throws an error.
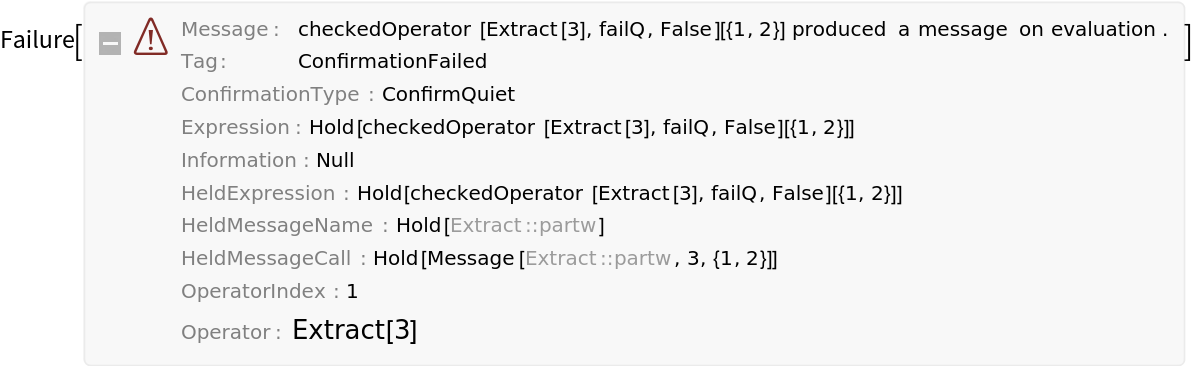
With the default setting "CatchMessages"→True, the pipeline will be aborted if a message is thrown. Messages are caught by using ConfirmQuiet.
The outputs of a computational network are those vertices that do not have any edged directed towards any other vertices (i.e., the vertices with VertexOutDegree equal to 0). If a computational networks has a single output vertex, it will return the value computed at that vertex. If it has multiple output vertices, it will return an Association with key-value pairs of the computed values at those vertices.
If a computational network has a vertex called "Input", the input to the network will always be supplied to that vertex.
If no "Input" vertex is specified, the input data must be an Association. The keys in that Association will specify the input vertices in the network. Keys that are absent from the pipeline, or that have in-degree different from zero will be ignored.
If multiple edges are directed at a single vertex in a computational network, the input to that vertex will be given as a list of the values computed at the vertices pointing into the target vertex. This is similar to the way NetGraph works.
Multiple values can be directed as a List to a vertex in the network either by specifying multiple rules {…,key1→target,key2→target, …} or by specifying a single rule of the form {…,{key1,key2,…}→target,…}.
If a key target does not have a specified operator associated to it, the operator will be taken to be Identity.
Chained rules like key1→key2→key3→… are allowed for the edge specification of a network. Rules of the form key1→{target1,target2,…} will be flattened out with Thread.
It is also possible to specify an input for a vertex as KeyTake[{key1,key2,…}] → target. In this case, data supplied to the target operator will be in the form of an Association with the keys keyi. This is useful when nesting computational networks inside each other.
In computational networks, the computations are evaluated in the order the edges are listed in.
You can specify default inputs for ResourceFunction["DataPipeline"] using generator functions. This is useful, for example, if you want the pipeline to automatically pull in data from an external source like a Databin whenever it is called. In linear pipelines, if the pipeline is called with no arguments, the first function will be evaluated with no arguments to generate the starting value of the pipeline. For computational networks, it is possible to specify multiple default generator functions in the first argument. If the input to the ResourceFunction["DataPipeline"] has keys corresponding to these generator functions, the specified input values will be used. Otherwise, the generator functions will be evaluated to generate the inputs on-the-fly. See the section Properties and Relations for examples.

Examples

Basic Examples (2) 

Define a chain of operations:

In[1]:=
pipeline = ResourceFunction["DataPipeline"][{Select[PrimeQ], Map[#^2 &], Total}]
Out[1]=

Apply it to a list:

In[2]:=
pipeline@Range[10]
Out[2]=

Visualize the data flow:

In[3]:=
Show[Information[pipeline, "Graph"], ImageSize -> 300]
Out[3]=

Nest existing pipelines into new ones:

In[4]:=
ResourceFunction[ "DataPipeline"][{Flatten, pipeline, Framed}][{{1}, {2, 3}, {4, 5, 6}}]
Out[4]=

Invalid intermediary results such as division by zero will cause a Failure to be thrown:

In[5]:=
ResourceFunction["DataPipeline"][{Select[EvenQ], Total, 1/# &, Sqrt}][ Range[-6, 6]]
Out[5]=

Scope (5) 

Steps in linear chains can be labeled:

In[6]:=
Information[ ResourceFunction[ "DataPipeline"][{"a" -> Select[PrimeQ], "b" -> Map[#^2 &], "c" -> Total}], "Graph"]
Out[6]=

Define and visualize a nonlinear data pipeline. Note that the "Input" vertex has a special meaning and is used to indicate where data enters the pipeline:

In[7]:=
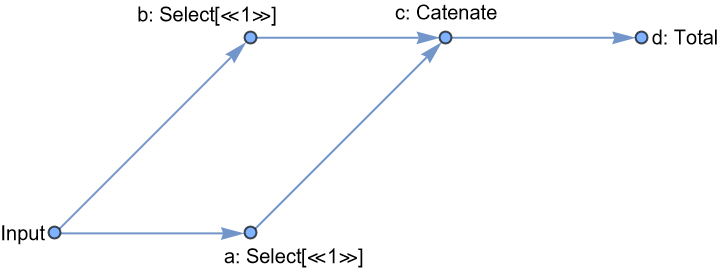
pipeline1 = ResourceFunction["DataPipeline"][ {"a" -> Select[EvenQ], "b" -> Select[PrimeQ], "c" -> Catenate, "d" -> Total}, {"Input" -> "a", "Input" -> "b", "a" -> "c", "b" -> "c", "c" -> "d"} ]; Information[pipeline1, "Graph"]
Out[8]=

Evaluate it:

In[9]:=
pipeline1@Range[10]
Out[9]=

Alternative method to specify the edges:

In[10]:=
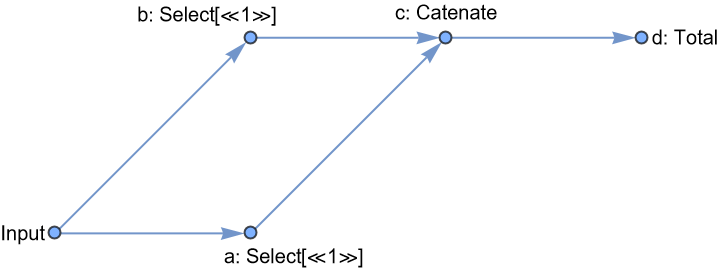
Information[ ResourceFunction[ "DataPipeline"][{"a" -> Select[EvenQ], "b" -> Select[PrimeQ], "c" -> Catenate, "d" -> Total}, {"Input" -> "a", "Input" -> "b", {"a", "b"} -> "c" -> "d"} ], "Graph"]
Out[10]=

Apply a nonlinear pipeline that has multiple inputs. Note that the input must be an Association in this case:

In[11]:=
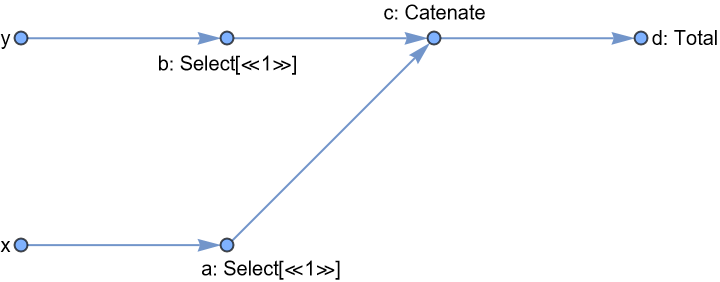
pipeline2 = ResourceFunction["DataPipeline"][ {"a" -> Select[EvenQ], "b" -> Select[PrimeQ], "c" -> Catenate, "d" -> Total}, {"x" -> "a", "y" -> "b", {"a", "b"} -> "c", "c" -> "d"} ]; pipeline2@<| "x" -> {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, "y" -> {37, 60, 80, 18, 61} |>
Out[12]=

Visualize it:

In[13]:=
Information[pipeline2, "Graph"]
Out[13]=

Apply a nonlinear pipeline that has multiple inputs and outputs. The output is returned as an Association:

In[14]:=
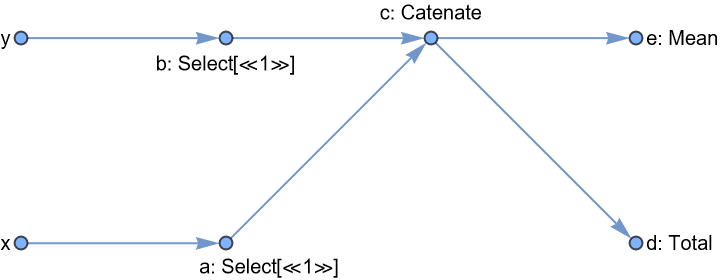
pipeline3 = ResourceFunction["DataPipeline"][ {"a" -> Select[EvenQ], "b" -> Select[PrimeQ], "c" -> Catenate, "d" -> Total, "e" -> Mean}, {"x" -> "a", "y" -> "b", {"a", "b"} -> "c", "c" -> "d", "c" -> "e"} ]; pipeline3@<| "x" -> {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, "y" -> {37, 60, 80, 18, 61} |>
Out[15]=

Visualize it:

In[16]:=
Information[pipeline3, "Graph"]
Out[16]=

Define a pipeline to use inside another pipeline:

In[17]:=
pipeline1 = ResourceFunction["DataPipeline"][ {"a" -> Select[EvenQ], "b" -> Select[PrimeQ], "c" -> Catenate, "d" -> Total}, {"x" -> "a", "y" -> "b", {"a", "b"} -> "c", "c" -> "d"} ]
Out[17]=

Nest it inside another one by using the KeyTake specification to link the keys in the outer pipeline to the inputs of the inner one:

In[18]:=
pipeLine2 = ResourceFunction["DataPipeline"][ { "x" -> Function[Range[#]], "y" -> Function[Range[#^3]], "pipe" -> pipeline1, "out" -> Framed }, {"Input" -> "x", "Input" -> "y", KeyTake[{"x", "y"}] -> "pipe", "pipe" -> "out"} ]
Out[18]=

Test it:

In[19]:=
pipeLine2[5]
Out[19]=

Options (4) 

FailureDetection (2) 

By default, Missing values are considered failures:

In[20]:=
ResourceFunction["DataPipeline"][{Lookup["a"], Total}]@<|"b" -> 1|>
Out[20]=

Specify that only explicit failures should be caught and let Query handle the missing values:

In[21]:=
ResourceFunction["DataPipeline"][{Lookup["a"], Query[Total]}, "FailureDetection" -> None]@<|"b" -> 1|>
Out[21]=

Values that satisfy FailureQ will always be considered a failure mode. You can use Failsafe to ensure that operations receive valid arguments:

In[22]:=
ResourceFunction["DataPipeline"][{Lookup["a"], Failsafe[Total, ListQ]}, "FailureDetection" -> None]@<|"b" -> 1|>
Out[22]=

By default, infinities are considered failure modes:

In[23]:=
ResourceFunction["DataPipeline"][{Lookup["a"], Log}]@<|"a" -> 0|>
Out[23]=

Specify explicitly that missing values should be considered failures, but allow infinities:

In[24]:=
ResourceFunction["DataPipeline"][{Lookup["a"], Log}, "FailureDetection" -> MissingQ]@<|"a" -> 0|>
Out[24]=

CatchMessages (2) 

By default, messages will be intercepted and returned as failures:

In[25]:=
ResourceFunction["DataPipeline"][{Extract[3], Sqrt}]@{1, 2}
Out[25]=

Use "CatchMessages"→False to continue the computation when messages are issued:

In[26]:=
ResourceFunction["DataPipeline"][{Extract[3], Sqrt}, "CatchMessages" -> False]@{1, 2}
Out[26]=

Properties and Relations (6) 

Define a pipeline with a generator function at the start:

In[27]:=
randomPipeline = ResourceFunction["DataPipeline"][{RandomReal[] &, Exp}]
Out[27]=

Evaluate it several times to generate different values:

In[28]:=
Table[randomPipeline[], 5]
Out[28]=

A computational network with random starting values:

In[29]:=
randomNetwork = ResourceFunction["DataPipeline"][ {"rand1" -> (RandomReal[] &), "rand2" -> (RandomChoice[{"x", "y"}] &), "a" -> Exp, "b" -> Function[# <> #], "c" -> Identity }, {"rand1" -> "a", "rand2" -> "b", {"a", "b"} -> "c"} ]
Out[29]=

Evaluate it:

In[30]:=
randomNetwork[]
Out[30]=

In a network you can override the random defaults with input values of your own choice:

In[31]:=
randomNetwork[<|"rand1" -> -1, "rand2" -> "z"|>]
Out[31]=

Only override one of the generated values:

In[32]:=
randomNetwork[<|"rand2" -> "z"|>]
Out[32]=

Publisher

Sjoerd Smit

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 05 March 2025

Related Resources

License Information