Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate the zero-order discrete prolate spheroidal sequence window
ResourceFunction["DPSSWindow"][n] gives the order-0 discrete prolate spheroidal sequence (DPSS) window of length n. | |
ResourceFunction["DPSSWindow"][n,α] uses the parameter α. |
A DPSS window of length 21:
| In[1]:= |
| Out[1]= |
Visualize the window:
| In[2]:= |
| Out[2]= |  |
A DPSS window with a specified parameter:
| In[3]:= |
| Out[3]= |
Create a lowpass FIR filter with cut-off frequency of π/5 and length 15:
| In[4]:= |
| Out[4]= |
Apply a DPSS window to the filter to improve stop-band attenuation:
| In[5]:= |
| Out[5]= |
Create a Log-magnitude plot of the power spectra of the two filters:
| In[6]:= |
| Out[6]= | 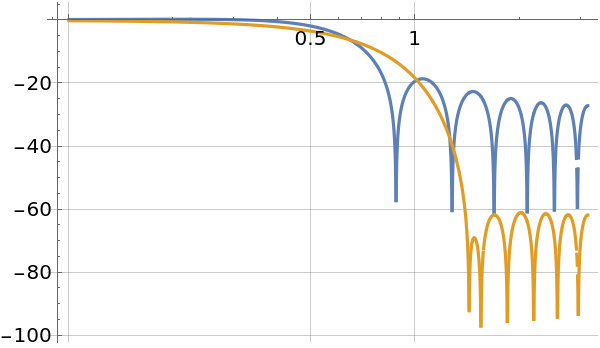 |
Use the DPSS window to diminish the effect of signal partitioning when computing the spectrogram:
| In[7]:= |
| Out[7]= |  |
DPSSWindow[n,0] is equivalent to the rectangular window:
| In[8]:= |
| Out[8]= |
The spectral concentration ratio of the DPSS window for length n and bandwidth -B<=ω<B:
| In[9]:= | ![n = 21; B = \[Pi]/10.;
w = ResourceFunction["DPSSWindow"][n, B];
W = ListFourierSequenceTransform[w, \[Omega]];
NIntegrate[Abs[W]^2, {\[Omega], -B, B}]/NIntegrate[
Abs[W]^2, {\[Omega], -\[Pi], \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/f33/f3365e02-00ad-4fb1-8c25-1d61993b8eb4/1d044f24c27910a7.png) |
| Out[12]= |
Compare with a Blackman window:
| In[13]:= | ![w = Array[BlackmanWindow, n, {-0.5, 0.5}];
W = ListFourierSequenceTransform[w, \[Omega]];
NIntegrate[Abs[W]^2, {\[Omega], -B, B}]/NIntegrate[
Abs[W]^2, {\[Omega], -\[Pi], \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/f33/f3365e02-00ad-4fb1-8c25-1d61993b8eb4/2a14245726801ad3.png) |
| Out[15]= |
This work is licensed under a Creative Commons Attribution 4.0 International License