Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CurveTorsion

Source Notebook

Compute the torsion of a curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["CurveTorsion"][c,t]

computes the torsion of a space curve c parametrized by t.

Details and Options

Torsion gives a measure of how rapidly a curve deviates from its osculating plane.

Examples

Basic Examples (4) 

Plot the twisted cubic curve:

In[1]:=
ParametricPlot3D[{t, t^2, t^3}, {t, -5, 5}]
Out[1]=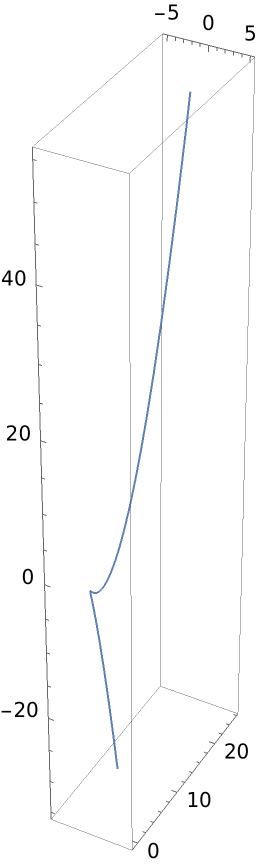

Compute the torsion of the twisted cubic curve:

In[2]:=
ResourceFunction["CurveTorsion"][{t, t^2, t^3}, t]
Out[2]=

Compute the curvature using the resource function Curvature:

In[3]:=
ResourceFunction["Curvature"][{t, t^2, t^3}, t]
Out[3]=

Plot them:

In[4]:=
Plot[{%, %%}, {t, 0, 1}]
Out[4]=

Scope (2) 

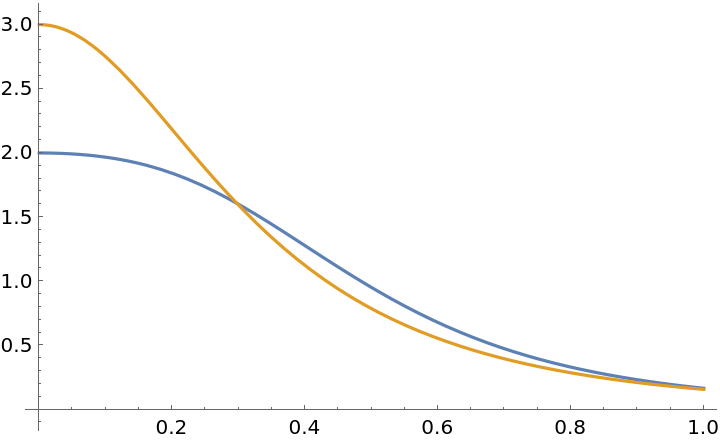For this curve, the torsion and curvature are the same:

In[5]:=
Simplify[ ResourceFunction["CurveTorsion"][{3 t - t^3, 3 t^2, 3 t + t^3}, t], t > 0]
Out[5]=
In[6]:=
Simplify[ ResourceFunction["Curvature"][{3*t - t^3, 3*t^2, 3*t + t^3}, t]]
Out[6]=

Plot of the above results:

In[7]:=
Plot[{%, %%}, {t, -2, 2}]
Out[7]=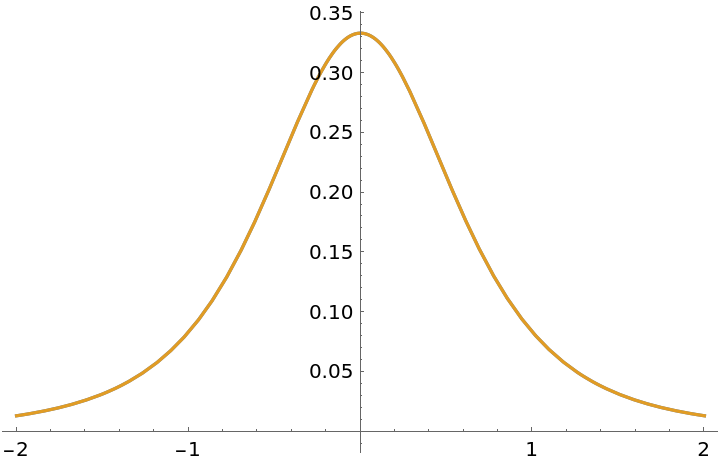

A curve that is qualitatively similar to a torus knot:

In[8]:=
tknot = {Cos[3 t], Cos[Sqrt[2] + 4 t], Cos[Sqrt[3] + 5 t]}
Out[8]=

Plot the curve:

In[9]:=
ParametricPlot3D[tknot, {t, 0, 2 \[Pi]}]
Out[9]=

Find the torsion:

In[10]:=
ResourceFunction["CurveTorsion"][tknot, t] // Simplify
Out[10]=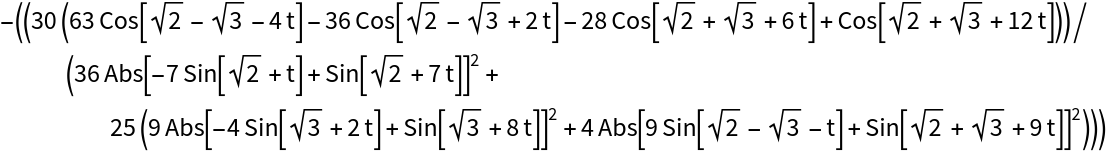

Plot this:

In[11]:=
Plot[%, {t, 0, 2 \[Pi]}]
Out[11]=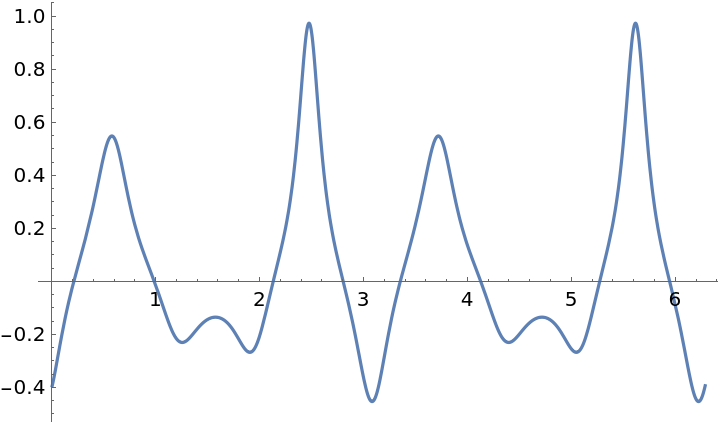

Compute the curvature with the resource function Curvature:

In[12]:=
Simplify[ResourceFunction["Curvature"][tknot, t]]
Out[12]=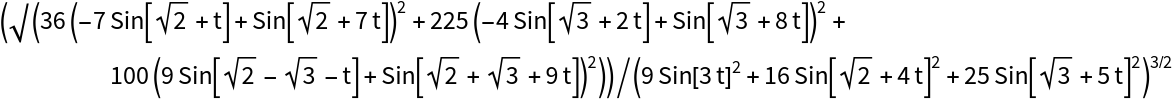
In[13]:=
Plot[%, {t, 0, 2 \[Pi]}]
Out[13]=

Properties and Relations (2) 

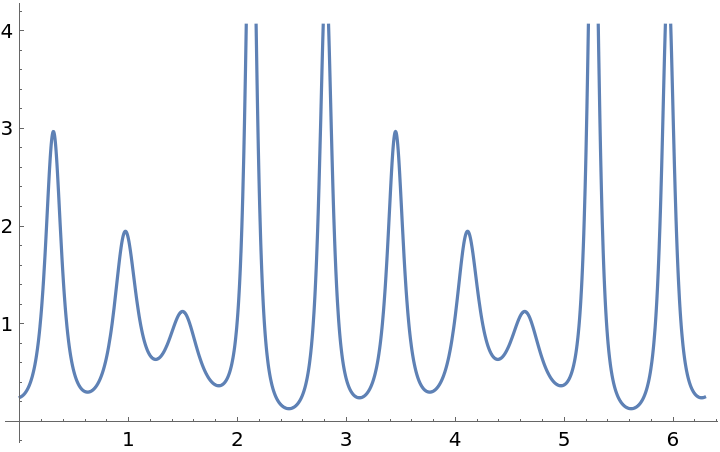Define a conical spiral:

In[14]:=
cs = Entity["SpaceCurve", "ConicalSpiral"]["ParametricEquations"][1, 1][t]
Out[14]=

Here is the torsion:

In[15]:=
\[Tau] = FullSimplify[ ResourceFunction["CurveTorsion"][{t Cos[t], t Sin[t], t}, t], t > 0]
Out[15]=

There are other quantities related to torsion. The inverse of the torsion is called the radius of torsion:

In[16]:=
1/\[Tau]
Out[16]=

The curvature, which can be calculated with the resource function Curvature:

In[17]:=
\[Kappa] = FullSimplify[ ResourceFunction["Curvature"][{t*Cos[t], t*Sin[t], t}, t]]
Out[17]=

There is also the so-called total curvature:

In[18]:=
FullSimplify[Sqrt[\[Kappa]^2 + \[Tau]^2], t > 0]
Out[18]=

Definition of a unit speed helix:

In[19]:=
uhelix = {a Cos[t/Sqrt[a^2 + b^2]], a Sin[t/Sqrt[a^2 + b^2]], (b t)/ Sqrt[a^2 + b^2]};

The curvature, via the resource function Curvature:

In[20]:=
\[Kappa] = Simplify[ResourceFunction["Curvature"][ uhelix, t], a > 0 && b > 0 && t > 0]
Out[20]=

The torsion:

In[21]:=
\[Tau] = Simplify[ResourceFunction["CurveTorsion"][uhelix, t], a > 0 && b > 0 && t > 0]
Out[21]=

The relation to the Frenet-Serret system is that the curvature and the torsion are the first two quantities:

In[22]:=
First@PowerExpand@Simplify@FrenetSerretSystem[uhelix, t]
Out[22]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 30 April 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information