Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Visualize the overlap of two discrete time series
ResourceFunction["CrossRecurrencePlot"][ts1,ts2] views the cross recurrence plot of the given time series ts1 and ts2. |
View the cross recurrence plot of two random lists:
| In[1]:= |
| Out[1]= |  |
View the cross recurrence plot of just one list of random integer values. Note the symmetry across the diagonal:
| In[2]:= |
| Out[2]= |  |
Visualize the cross recurrence plot of the Sinc function with a recurrence type of "Global":
| In[3]:= |
| Out[3]= |  |
View the cross recurrence plot of a range and a random list of integers:
| In[4]:= |
| Out[4]= | 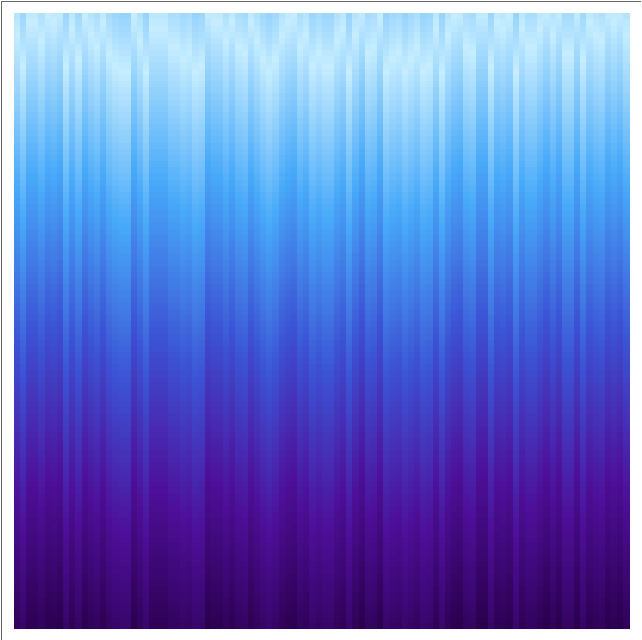 |
View a cross recurrent plot of equal ranges:
| In[5]:= |
| Out[5]= |  |
View a cross recurrence plot of two different small lists:
| In[6]:= |
| Out[6]= |  |
View a cross recurrence plot of a range and a short list of integers:
| In[7]:= |
| Out[7]= |  |
View the cross recurrence plot of discrete values of Sin and Cos:
| In[8]:= |
| Out[8]= |  |
View a cross recurrence plot of two lists of different sizes:
| In[9]:= |
| Out[9]= |  |
We can analyse time series behavior by cross recurrence plots. In this case we combine sine and cosine to create and visualize two different time series:
| In[10]:= | ![Manipulate[GraphicsGrid[{{ListLinePlot[{
s1 = Table[Sin[x f1x]*Cos[x f1y], {x, -10, 10, .1}],
s2 = Table[Sin[y f2x]*Cos[y f2y], {y, -10, 10, .1}]}],
ResourceFunction["CrossRecurrencePlot"][s1, s2, Frame -> None]}}],
{f1x, 1, 10},
{f1y, 1, 10},
{{f2x, 5}, 1, 10},
{{f2y, 7}, 1, 10}]](https://www.wolframcloud.com/obj/resourcesystem/images/63d/63df4aa1-9e01-416e-9af0-14b42891edfb/174cee5f0f848e4b.png) |
| Out[10]= | 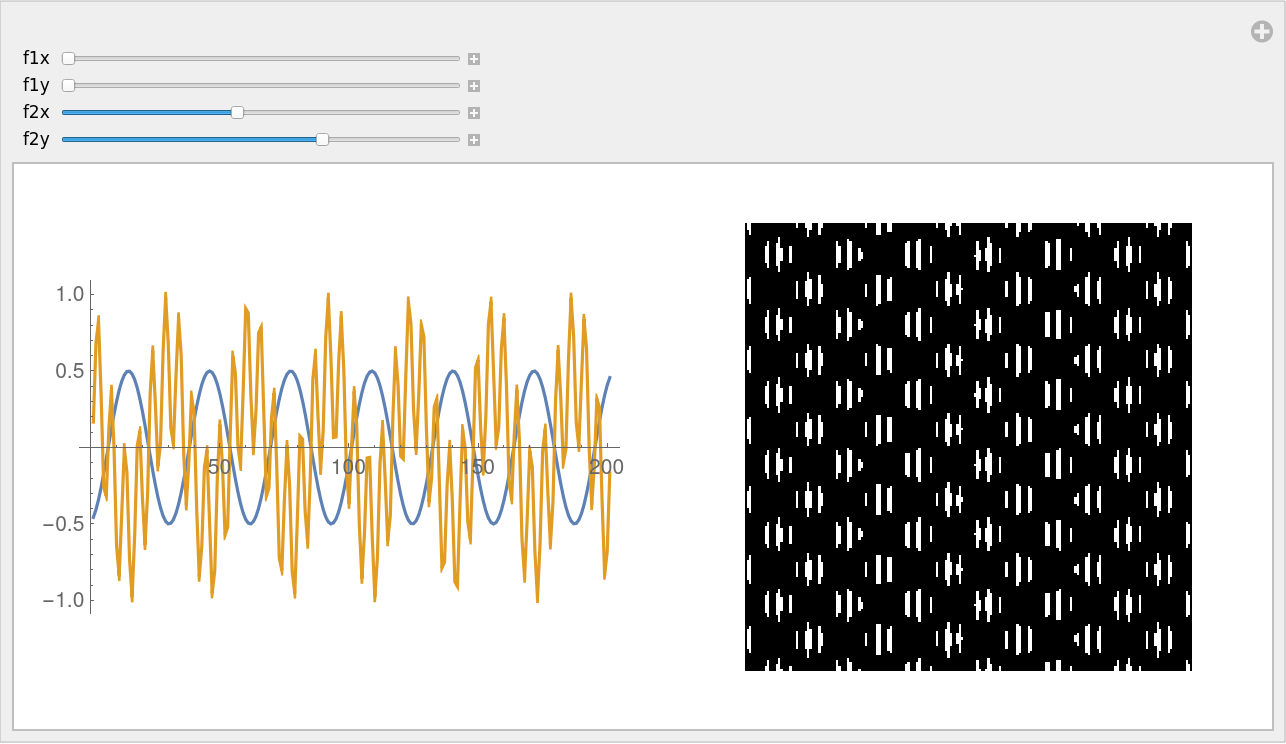 |
To compare and analyse the dynamical behaviour of two elementary cellular automata rules we can plot them, count the total number of black cells by steps, and them show the global cross recurrence plot. Note that when we select the same rule for the two cellular automata, we see diagonal symmetry:
| In[11]:= | ![Manipulate[SeedRandom[92177];
init = RandomInteger[1, 100];
GraphicsGrid[{{ArrayPlot[ca1 = CellularAutomaton[rule1, init, 100], Frame -> None],
ArrayPlot[ca2 = CellularAutomaton[rule2, init, 100], Frame -> None]},
{ListLinePlot[{
ca1dynamics = Total[Transpose[ca1]],
ca2dynamics = Total[Transpose[ca2]]}],
ResourceFunction["CrossRecurrencePlot"][ca1dynamics, ca2dynamics, Frame -> None, RecurrenceType -> "Global", ColorFunction -> Hue]}}],
{{rule1, 30}, 0, 255, 1},
{{rule2, 110}, 0, 255, 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/63d/63df4aa1-9e01-416e-9af0-14b42891edfb/5e4c716bb71f2f96.png) |
| Out[11]= | 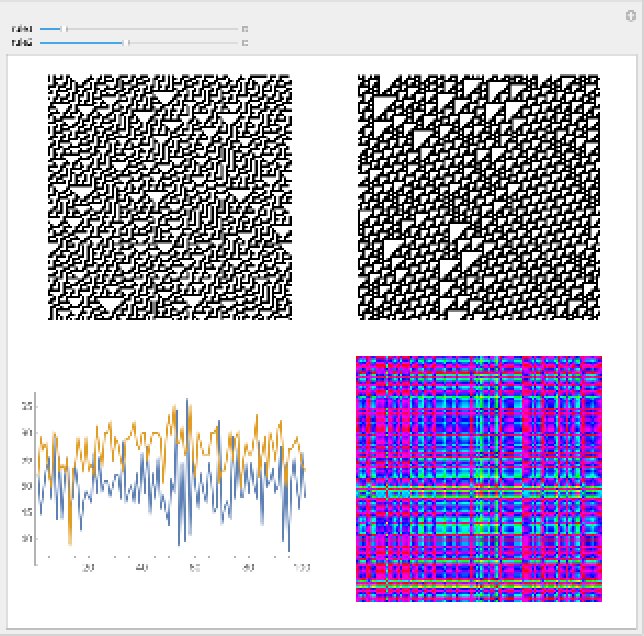 |
This work is licensed under a Creative Commons Attribution 4.0 International License