Function Repository Resource:

CrossNodeGridGraph

Source Notebook

Create cross-linked grid graphs

Contributed by: Utkarsh Patel and Simon Fischer

ResourceFunction["CrossNodeGridGraph"][r,d]

creates a d-dimensional grid graph with r cross-linked vertices in all dimensions.

ResourceFunction["CrossNodeGridGraph"][{n₁,n₂,…,n_d}]

creates a d-dimensional grid graph with n_i cross-linked vertices in each dimension.

Details and Options

ResourceFunction["CrossNodeGridGraph"] can be used to create fractional dimension hypergraphs.

ResourceFunction["CrossNodeGridGraph"] has the same options as Graph, with the following additions and changes:

"CoordinateLabeled"

True

whether to change vertex labels to a Cartesian coordinate system with the central vertex as origin

VertexLabels

Automatic

labels and placements for vertices

VertexSize

Tiny

size of vertices

With the setting VertexCoordinates→Automatic, the vertices are laid out in an orthogonal grid for dimensions 2 and 3.

Examples

Basic Examples (2)

A 2-dimensional cross-linked grid graph:

In[1]:=

Out[1]=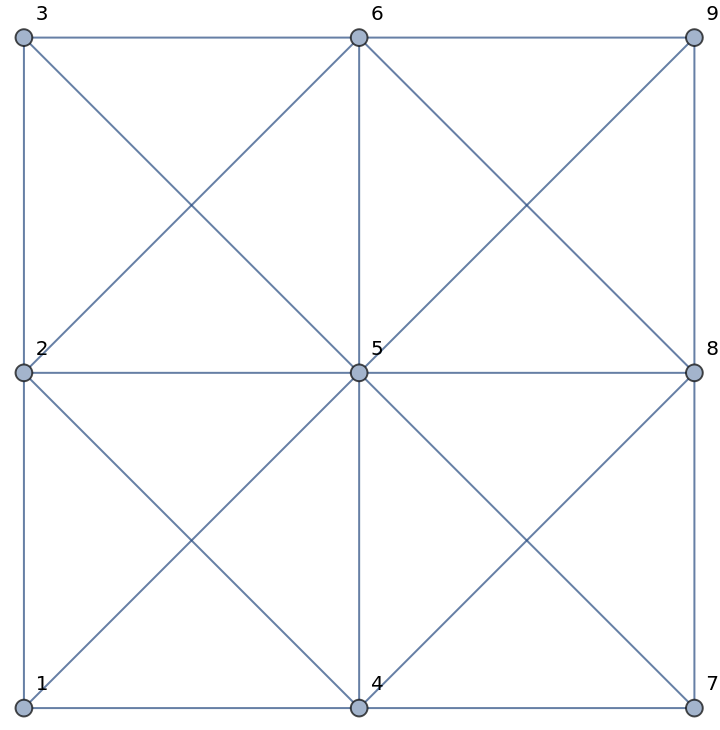

A 3-dimensional cross-linked grid graph:

In[2]:=

Out[2]=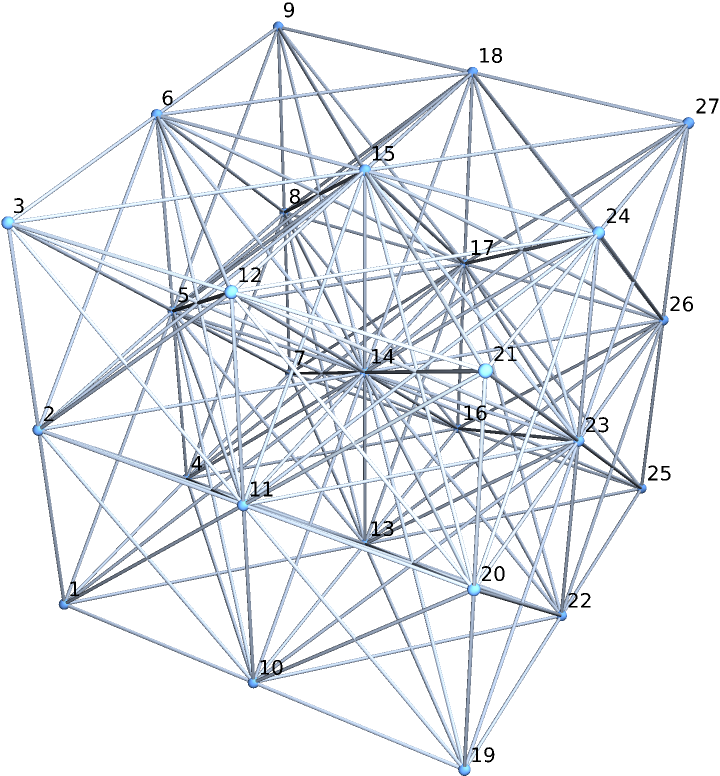

Scope (2)

A 5-dimensional cross-linked grid graph, embedded in 3D:

In[3]:=

Out[3]=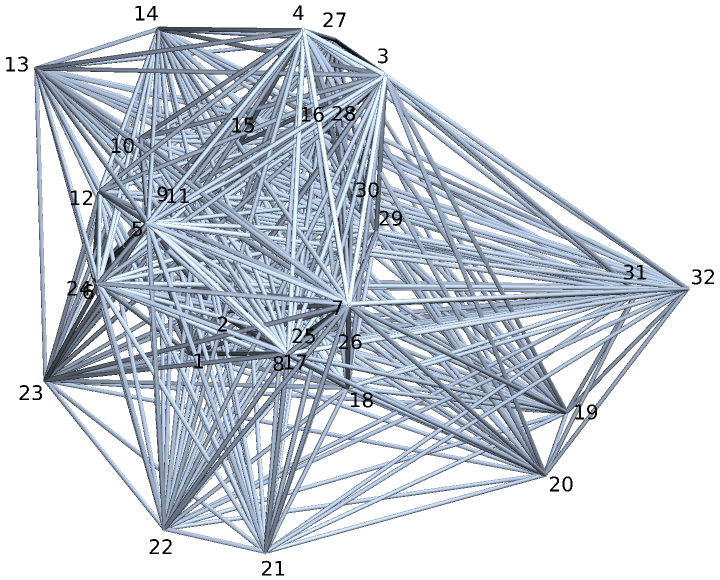

A 2-dimensional rectangular cross-linked grid graph:

In[4]:=

Out[4]=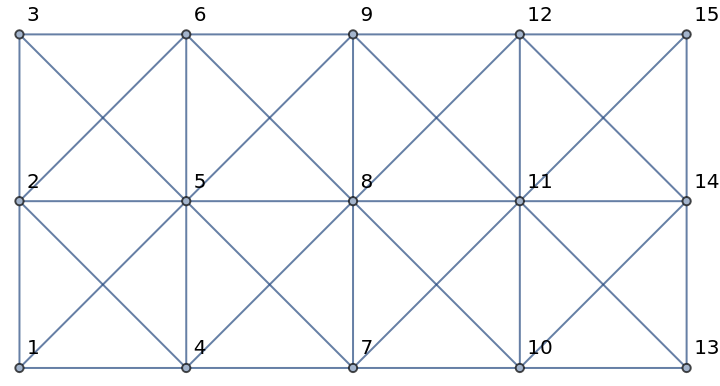

Options (2)

CoordinateLabeled (2)

With "CoordinateLabeled"->False, the vertex labels are set as their indices:

In[5]:=

Out[5]=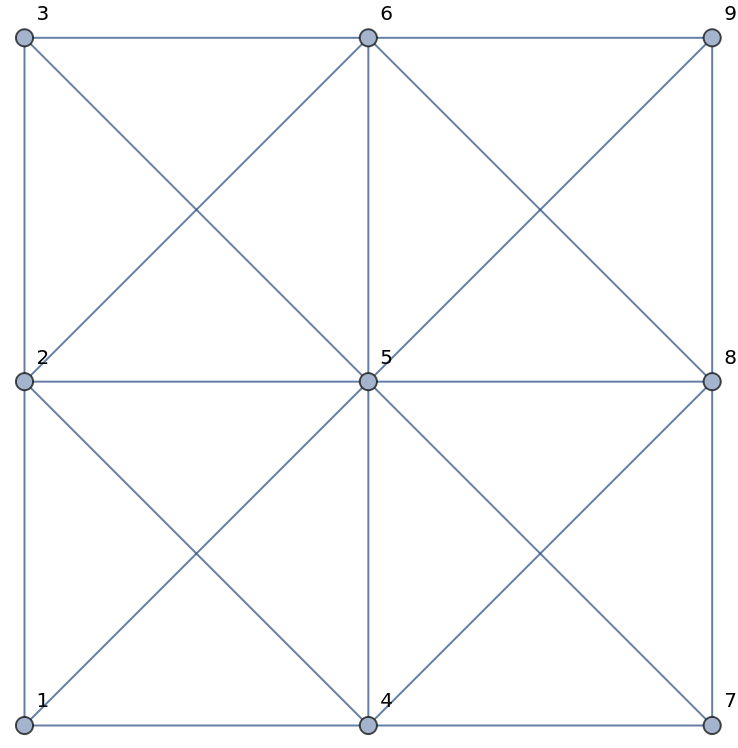

With "CoordinateLabeled"->True, the vertex labels are set as their Cartesian coordinates:

In[6]:=

Out[6]=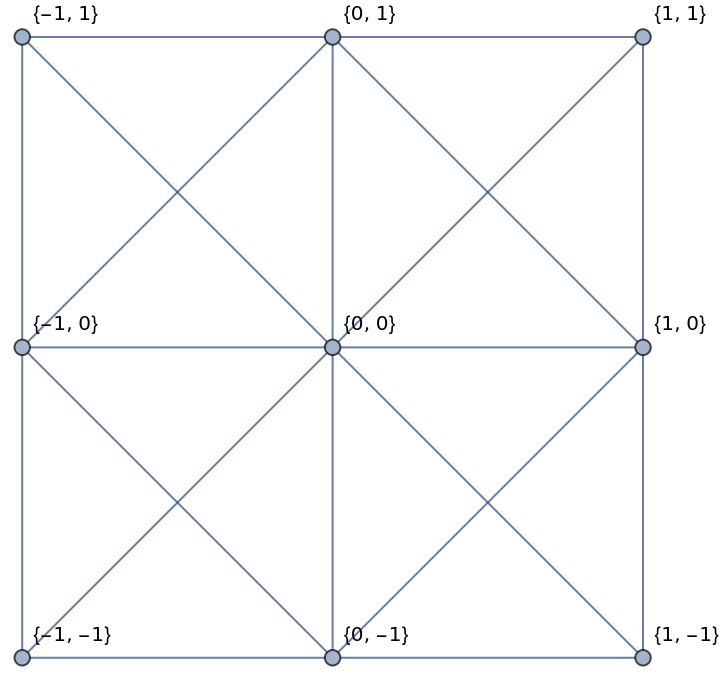

A 3-dimensional cross-linked grid graph with vertices labeled as their Cartesian coordinates:

In[7]:=

Out[7]=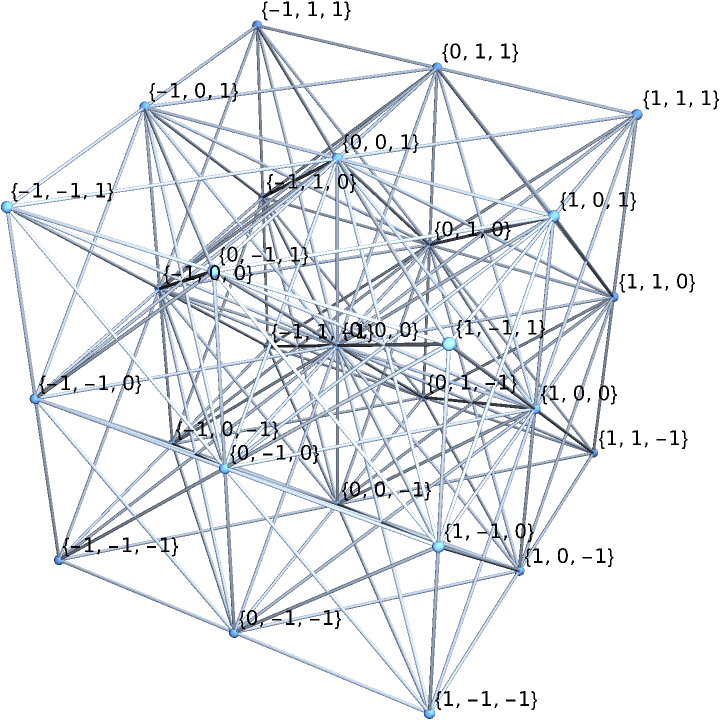

Properties and Relations (3)

CrossNodeGridGraph[r,d] is equivalent to CrossNodeGridGraph[ConstantArray[r,d]]:

In[8]:=

Out[8]=

The tetrahedral graph is a special case of CrossNodeGridGraph:

In[9]:=

Out[9]=

CompleteGraph is a special case of CrossNodeGridGraph:

In[10]:=

$Table[IsomorphicGraphQ[ResourceFunction["CrossNodeGridGraph"][2, k], CompleteGraph[2^k]], {k, 2, 5}]$

Out[10]=

Neat Examples (2)

Visualize a perspective projection of a 4D cross-linked grid graph:

In[11]:=

g = ResourceFunction["CrossNodeGridGraph"][2, 4, "CoordinateLabeled" -> True];
Graph3D[IndexGraph[g], VertexCoordinates -> (Delete[2 # + 1, 3]/(3 - 2 Extract[#, 3]) & /@ VertexList[g])]

Out[12]=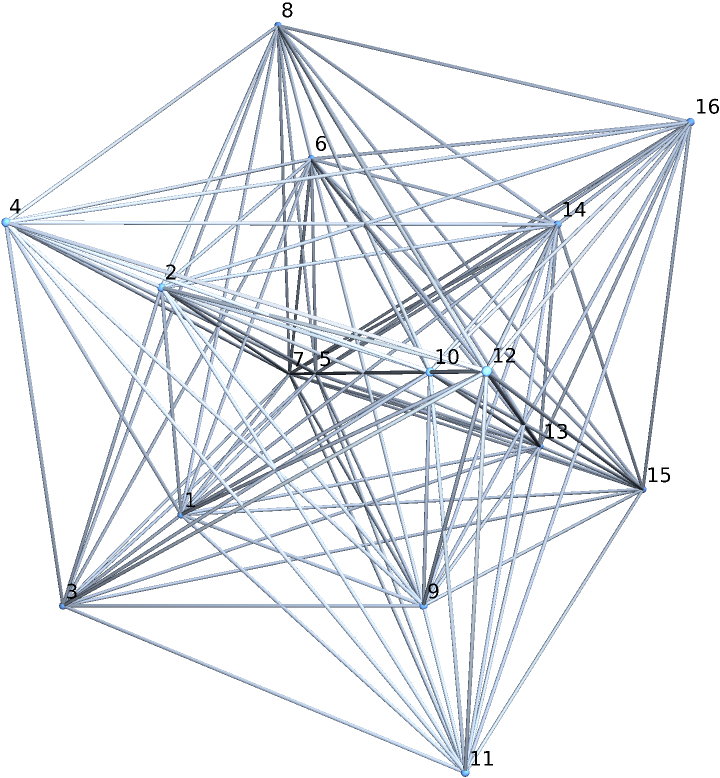

Create a 2D cross-linked grid graph:

In[13]:=

Out[13]=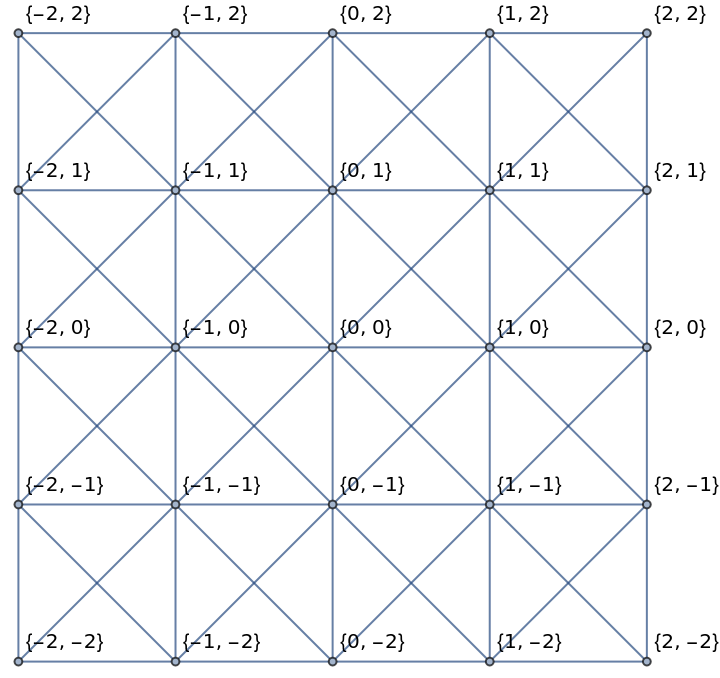

The resource function WolframHausdorffDimension can be used to verify that the dimensionality of the graph's vertices are of fractional order:

In[14]:=

Out[14]=

In[15]:=

Out[15]=

Publisher

Utkarsh Patel

Version History

1.0.0 – 25 July 2022

Source Metadata

Citation:
- Stephen Wolfram (2002), A New Kind of Science
- Stephen Wolfram (2020), "A Class of Models with the Potential to Represent Fundamental Physics"
- Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model"
- Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model"

Related Resources

Author Notes

The function can currently create cross-link graphs for 2D and 3D only.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

CrossNodeGridGraph

Details and Options