Function Repository Resource:

CreateSortableUniqueID

Source Notebook

Create a K-Sortable Unique Identifiers hexadecimal string

Contributed by: Daniel de Souza Carvalho

ResourceFunction["CreateSortableUniqueID"][]

retrieves a hexadecimal unique partial sortable ID string.

ResourceFunction["CreateSortableUniqueID"][n]

retrieves a list of n hexadecimal unique partial sortable ID strings.

Details

A K-Sortable Unique Identifier (KSUID) is a partially sortable type of identifier.

The algorithm to create KSUIDs produces hexadecimal strings that are statistically unlikely to repeat.

A KSUID is comprised of two parts. The first eight characters are from a timestamp and can be sorted lexicographically. The remainder is a random 19 character hexadecimal string.

KSUIDs can be sorted because the timestamp parts are at the beginning. This is only a partial ordering because there is a (very small) possibility that the random parts of two KSUIDs can agree.

This function can be used to provide identifiers to NoSQL database documents (JSON) in working with unstructured data and objects.

The time stamp uses the current time zone.

Examples

Basic Examples (2)

Get one unique KSUID:

In[1]:=

Out[1]=

Get a list of unique IDs:

In[2]:=

Out[2]=

Scope (1)

The beginning of a set of IDs are close to one another because they are based on Unix timestamps, while the second parts are pseudorandom hex digits:

In[3]:=

Out[3]=

Applications (2)

We can check when a set of IDs were created:

In[4]:=

SKUIDsample =
{"0ujsszwN8NRY24YaXiTIE2VWDTS",
"0ujsswThIGTUYm2K8FjOOfXtY1K",
"0ujssxh0cECutqzMgbtXSGnjorm",
"0ujsszgFvbiEr7CDgE3z8MAUPFt"};

Take the first eight hexadecimal digits, converting to decimal and converting from Unix time format:

In[5]:=

Out[5]=

Properties and Relations (6)

It is possible to recover the timestamp from an ID, step by step:

In[6]:=

Out[6]=

Take just the 8 initial characters:

In[7]:=

Out[7]=

Convert the hexadecimal to integer:

In[8]:=

Out[8]=

Convert from Unix time format:

In[9]:=

Out[9]=

Compare with the value of a current Unix time:

In[10]:=

Out[10]=

Validate the timestamp at the beginning of the hash:

In[11]:=

Out[11]=

Neat Examples (2)

Breaking the IDs into 2 hexadecimal pairs, we can plot the IDs as a graph, and view the random and repetitive parts:

In[12]:=

Out[12]=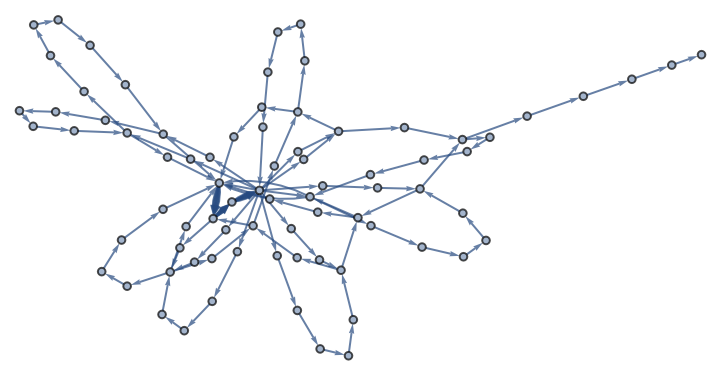

We can view a set of IDs as an image:

In[13]:=

Out[13]=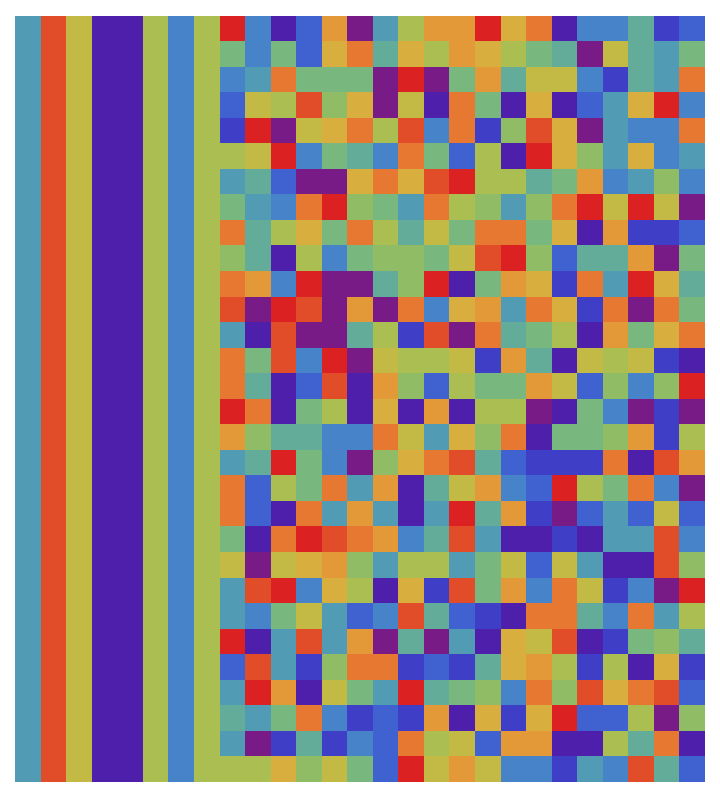

We can likewise view a sorted set of IDs as an image:

In[14]:=

Out[14]=

Publisher

Daniel de Souza Carvalho

Version History

1.0.0 – 15 July 2022

Source Metadata

Citation:
- Jesus, P., Baquero, C., Almeida, P., "ID Generation in Mobile Environments." Conference paper, 2006. http://hdl.handle.net/1822/36065
- Altman, T., Igarashi, Y., "Roughly sorting: sequential and parallel approach." Journal of Information Processing, vol. 12, no. 2, 154–158, 1989. http://id.nii.ac.jp/1001/00059782/

Related Resources

Author Notes

KSUID generates globally unique IDs close to RFC 4122 UUIDs, with a time component at the beginning of the hexadecimal value, in order to be “roughly” sorted by time of creation. This algorithm is statistically hard to get repeated values.

License Information

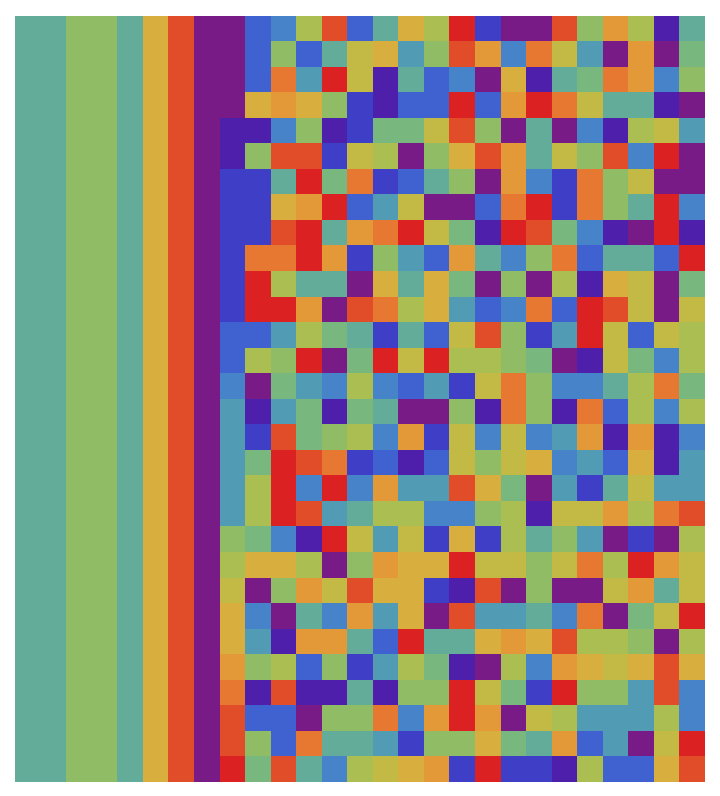This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

CreateSortableUniqueID

Details