Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language
This resource function is obsolete. Use the function CoulombF instead.

Function Repository Resource:

 CoulombF

Source Notebook

Evaluate the regular Coulomb wavefunction

Contributed by: Jan Mangaldan

ResourceFunction["CoulombF"][l,η,ρ]

gives the regular Coulomb wavefunction Fl(η,ρ).

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
Fl(η,ρ) satisfies the Coulomb wave differential equation ρ2∂{ρ,2}w+(ρ2-2ηρ-l(l+1))w=0.
For certain special arguments, ResourceFunction["CoulombF"] automatically evaluates to exact values.
ResourceFunction["CoulombF"] can be evaluated to arbitrary numerical precision.
ResourceFunction["CoulombF"] automatically threads over lists.

Examples

Basic Examples (3) 

Evaluate numerically:

In[1]:=
ResourceFunction["CoulombF"][0, 2, 7.1]
Out[1]=

Plot F0(-2,ρ) over a subset of the reals:

In[2]:=
Plot[ResourceFunction["CoulombF"][0, -2, x], {x, 0, 20}]
Out[2]=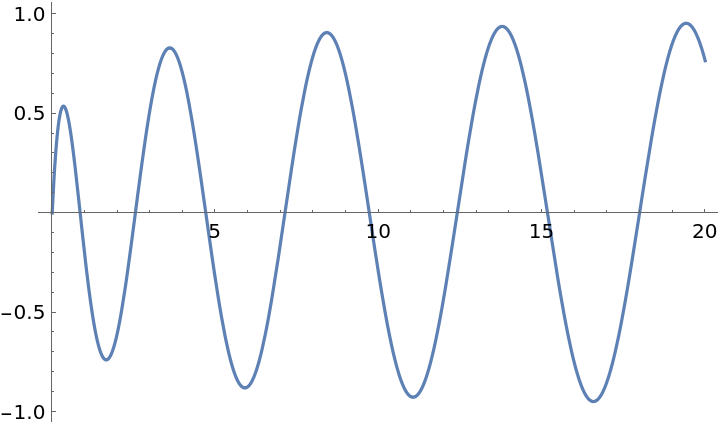

Series expansion at the origin:

In[3]:=
Series[ResourceFunction["CoulombF"][0, 0, \[Rho]], {\[Rho], 0, 9}]
Out[3]=

Scope (4) 

Evaluate for complex arguments:

In[4]:=
ResourceFunction["CoulombF"][-0.7 I, 2.1 + 1.3 I, 0.3 + 0.4 I]
Out[4]=

Evaluate to high precision:

In[5]:=
N[ResourceFunction["CoulombF"][1, 5/2, 11/3], 25]
Out[5]=

The precision of the output tracks the precision of the input:

In[6]:=
ResourceFunction["CoulombF"][1, 2.500000000000000000000000000, 11/3]
Out[6]=

CoulombF threads elementwise over lists:

In[7]:=
ResourceFunction["CoulombF"][{1, 2, 3}, 1/2, 4.4]
Out[7]=

Simple exact values are generated automatically:

In[8]:=
ResourceFunction["CoulombF"][1, -3, 0]
Out[8]=

Applications (1) 

Plot CoulombF as a function of ρ and η:

In[9]:=
Plot3D[ResourceFunction["CoulombF"][0, \[Eta], \[Rho]], {\[Rho], 0, 5}, {\[Eta], -2, 2}, ColorFunction -> (Hue[2 (1 - #3)/3] &), {Mesh -> False, PlotPoints -> 75, WorkingPrecision -> 20}]
Out[9]=

Properties and Relations (3) 

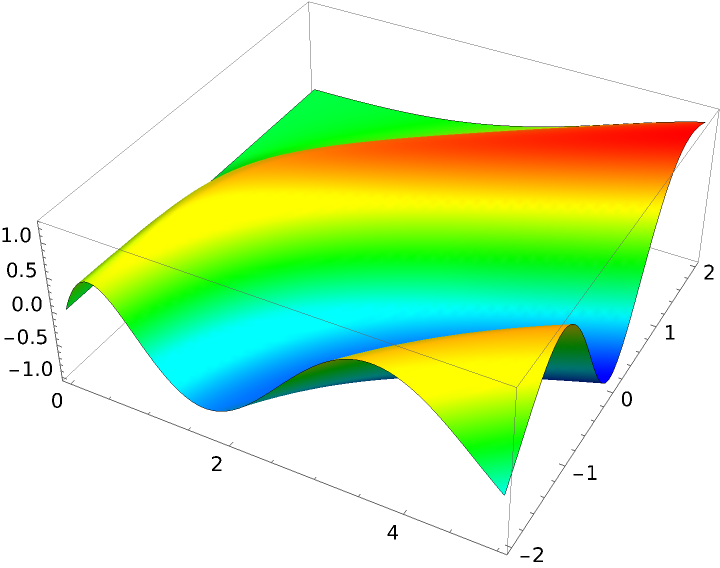CoulombF satisfies a differential equation:

In[10]:=
\!\( \*SubscriptBox[\(\[PartialD]\), \({\[Rho], 2}\)]\(\* InterpretationBox[ TagBox[ DynamicModuleBox[{Typeset`open = False}, FrameBox[ PaneSelectorBox[{False->GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["CoulombF", "ResourceFunctionLabel"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"], ImageSizeCache->{11., {1., 10.}}], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"], ImageSizeCache->{11., {1., 10.}}]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}], True->GridBox[{ {GridBox[{ { PaneBox[GridBox[{ { StyleBox[ StyleBox[ AdjustmentBox["\<\"[\[FilledSmallSquare]]\"\>", BoxBaselineShift->-0.25, BoxMargins->{{0, 0}, {-1, -1}}], "ResourceFunctionIcon", FontColor->RGBColor[ 0.8745098039215686, 0.2784313725490196, 0.03137254901960784]], ShowStringCharacters->False, FontFamily->"Source Sans Pro Black", FontSize->0.6538461538461539 Inherited, FontWeight->"Heavy", PrivateFontOptions->{"OperatorSubstitution"->False}], StyleBox[ RowBox[{ StyleBox["CoulombF", "ResourceFunctionLabel"], " "}], ShowAutoStyles->False, ShowStringCharacters->False, FontSize->Rational[12, 13] Inherited, FontColor->GrayLevel[0.1]]} }, GridBoxSpacings->{"Columns" -> {{0.25}}}], Alignment->Left, BaseStyle->{LineSpacing -> {0, 0}, LineBreakWithin -> False}, BaselinePosition->Baseline, FrameMargins->{{3, 0}, {0, 0}}], ItemBox[ PaneBox[ TogglerBox[Dynamic[Typeset`open], {True-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeCloser"]], False-> DynamicBox[FEPrivate`FrontEndResource["FEBitmaps", "IconizeOpener"]]}, Appearance->None, BaselinePosition->Baseline, ContentPadding->False, FrameMargins->0], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{1, 1}, {0, 0}}], Frame->{{ RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627, 0.5], False}, {False, False}}]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}, GridBoxSpacings->{"Columns" -> {{0}}, "Rows" -> {{0}}}]}, { StyleBox[ PaneBox[GridBox[{ { RowBox[{ TagBox["\<\"Version (latest): \"\>", "IconizedLabel"], " ", TagBox["\<\"1.1.0\"\>", "IconizedItem"]}]}, { TagBox[ TemplateBox[{"\"Documentation »\"", "https://resources.wolframcloud.com/FunctionRepository/resources/90e04d69-1484-41f1-951c-f4483a2fccf4/"}, "HyperlinkURL"], "IconizedItem"]} }, DefaultBaseStyle->"Column", GridBoxAlignment->{"Columns" -> {{Left}}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}], Alignment->Left, BaselinePosition->Baseline, FrameMargins->{{5, 4}, {0, 4}}], "DialogStyle", FontFamily->"Roboto", FontSize->11]} }, BaselinePosition->{1, 1}, GridBoxAlignment->{"Columns" -> {{Left}}, "Rows" -> {{Baseline}}}, GridBoxDividers->{"Columns" -> {{None}}, "Rows" -> {False, { GrayLevel[0.8]}, False}}, GridBoxItemSize->{"Columns" -> {{Automatic}}, "Rows" -> {{Automatic}}}]}, Dynamic[Typeset`open], BaselinePosition->Baseline, ImageSize->Automatic], Background->RGBColor[ 0.9686274509803922, 0.9764705882352941, 0.984313725490196], BaselinePosition->Baseline, DefaultBaseStyle->{}, FrameMargins->{{0, 0}, {1, 0}}, FrameStyle->RGBColor[ 0.8313725490196079, 0.8470588235294118, 0.8509803921568627], RoundingRadius->4]], {"FunctionResourceBox", RGBColor[0.8745098039215686, 0.2784313725490196, 0.03137254901960784], "CoulombF"}, TagBoxNote->"FunctionResourceBox"], ResourceFunction["CoulombF"], BoxID -> "CoulombF", Selectable->False][\[ScriptL], \[Eta], \[Rho]]\)\) + (1 - ( 2 \[Eta])/\[Rho] - (\[ScriptL] (\[ScriptL] + 1))/\[Rho]^2) ResourceFunction[ "CoulombF"][\[ScriptL], \[Eta], \[Rho]] == 0 // FullSimplify
Out[10]=

CoulombF satisfies a recurrence relation:

In[11]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/57d1edf9-2b48-4b13-bddb-360abc8ecc1a"]
Out[11]=

Express the derivative of CoulombF in terms of CoulombF:

In[12]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/3013c295-4258-4c1f-818f-f7b7843d5e94"]
Out[12]=
In[13]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9f50c6d7-ec84-436e-8ef4-4cf448b634c0"]
Out[13]=

Version History

  • 1.1.0 – 13 September 2021
  • 1.0.0 – 03 March 2021

Source Metadata

  • Citation:
    • "Coulomb Functions Functions." Chapter 33 in F. W. J. Olver et al. (eds.), NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov/33. Release 1.1.6 of 2022-06-30.
    • Humblet J., "Analytical structure and properties of Coulomb wave functions for real and complex energies." Annals of Physics, vol. 155, no. 2, 461-493, 1984. DOI: 10.1016/0003-4916(84)90009-5
    • Thompson I.J., Barnett A.R., "Coulomb and Bessel functions of complex arguments and order." Journal of Computational Physics, vol. 64, no. 2, 490-509, 1986. DOI: 10.1016/0021-9991(86)90046-X

Related Resources

License Information