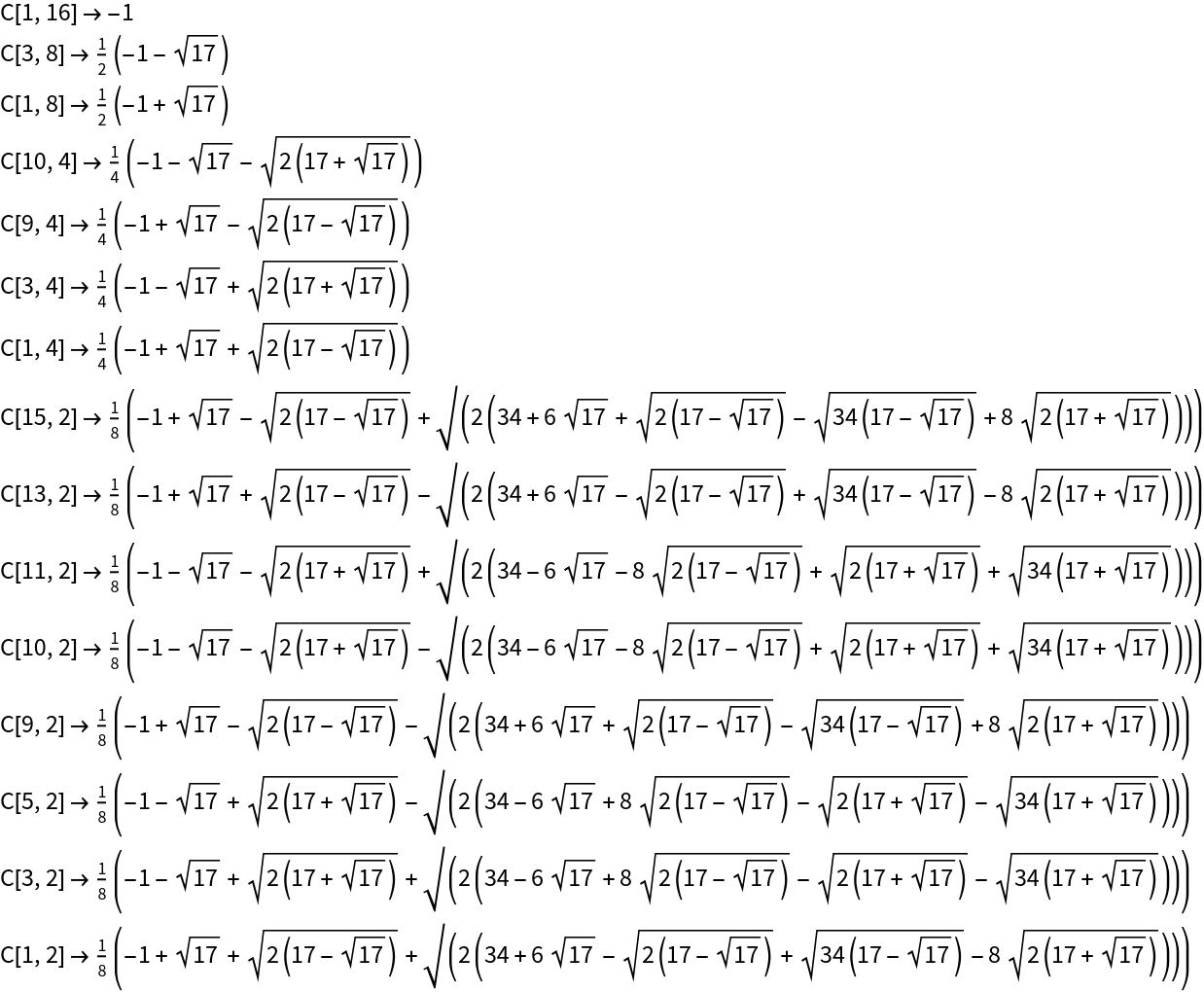Basic Examples (3)
The classic Gauss result for cos(2π/17):
Using the "Rules" argument shows the recursive nature of the period values:
Applying the rules gives the above expression once again:
The cosine values for the two smallest Fermat primes:
Scope (1)
Cos2PiOverFermatPrime gives results for all the basic trig functions:
Options (2)
The default parameter is C:
Use subscripts for the period values:
Applications (4)
The case p=257 was manually computed by Richelot in 1832:
cos(2π/257):
The expression contains more than 5,100 square roots:
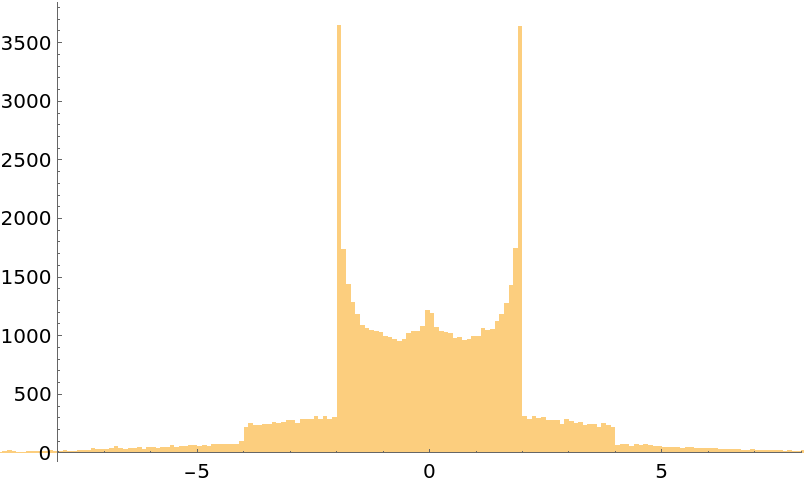
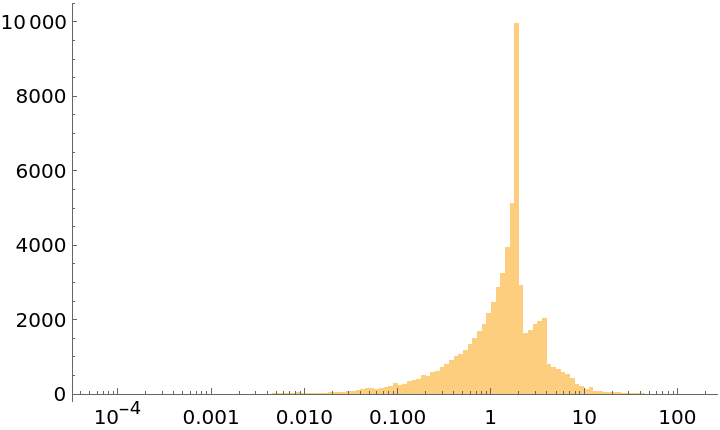
Plot the frequency of occurrences of different square roots (mouseover points to see square roots):
The network of the period values of cos(2π/257):
Visualize with a graph:
Find the explicit numerical values of all periods:
Properties and Relations (2)
The function ToRadicals does express cos(2π/257) in radicals, but not in square roots:
ToRadicals of cos(2π/17) returns an expression quite similar to Cos2PiOverFermatPrime:
Possible Issues (1)
The computation for the Fermat prime 65,537 will take about 10 to 15 min on a modern laptop:
Neat Examples (5)
The value of cos(2π/65537) was first computed by Johann Gustav Hermes and took him 10 years. The computation are still preserved in the famous "suitcase of Göttingen":
The length of the rule list is p-2:
To compute the period values, we change the rules to assignments and let the 65,535 assignments autoevaluate after numericalization of numbers:
The last value is just cos(2π/65537):
Plot the distribution of the 65,535 period values on a linear and on a logarithmic scale:
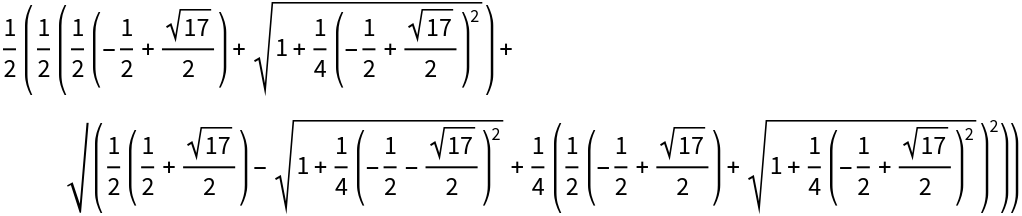

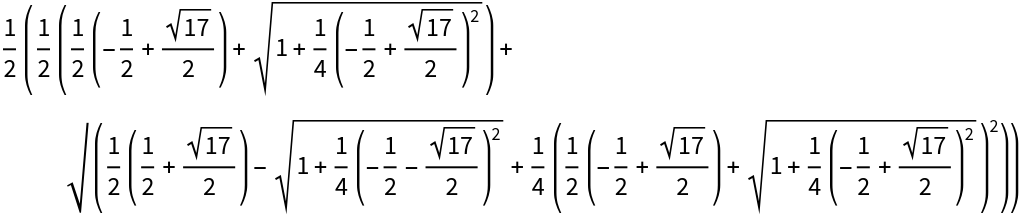
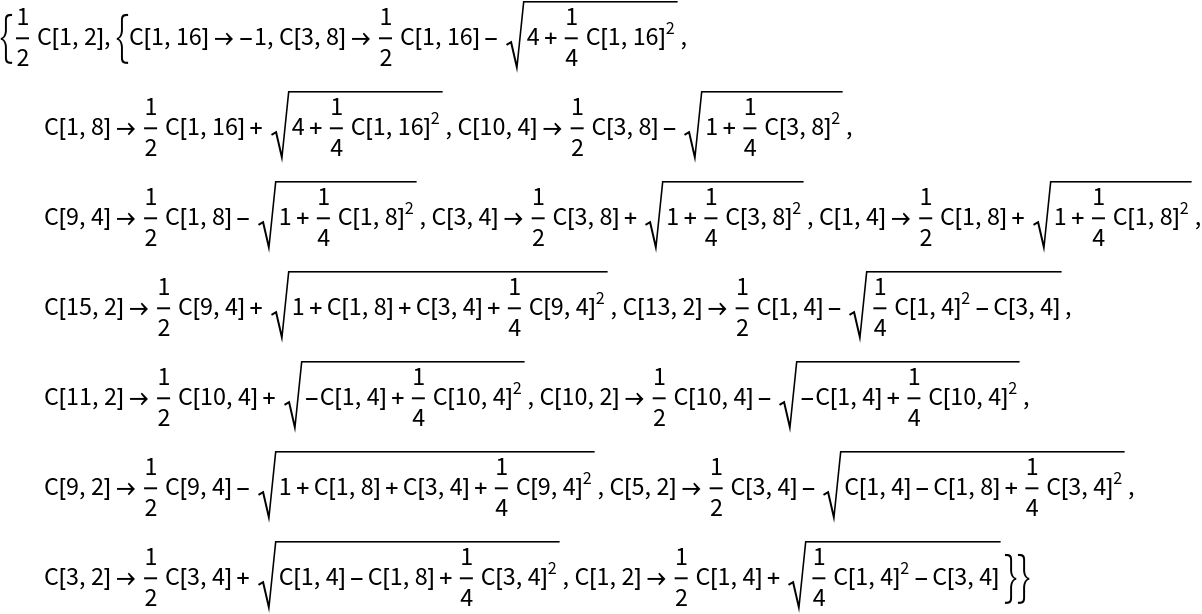
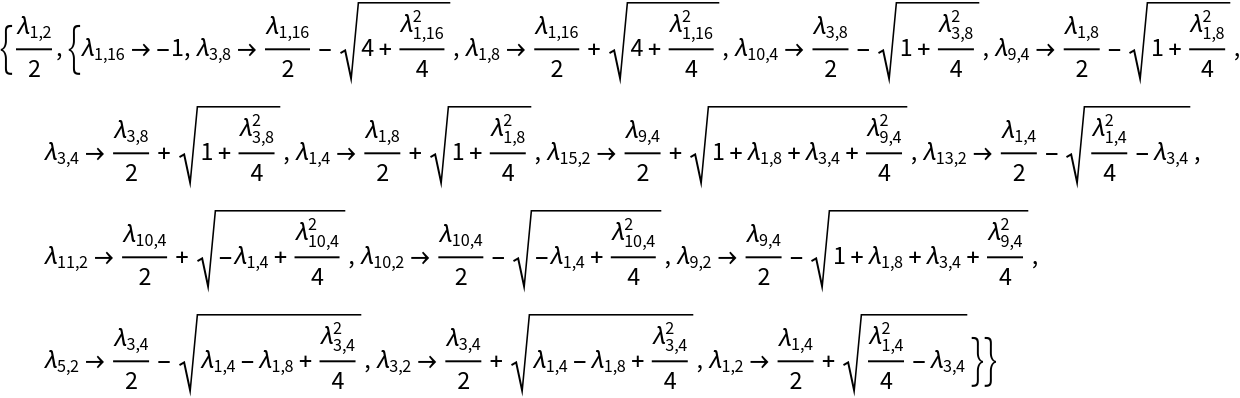




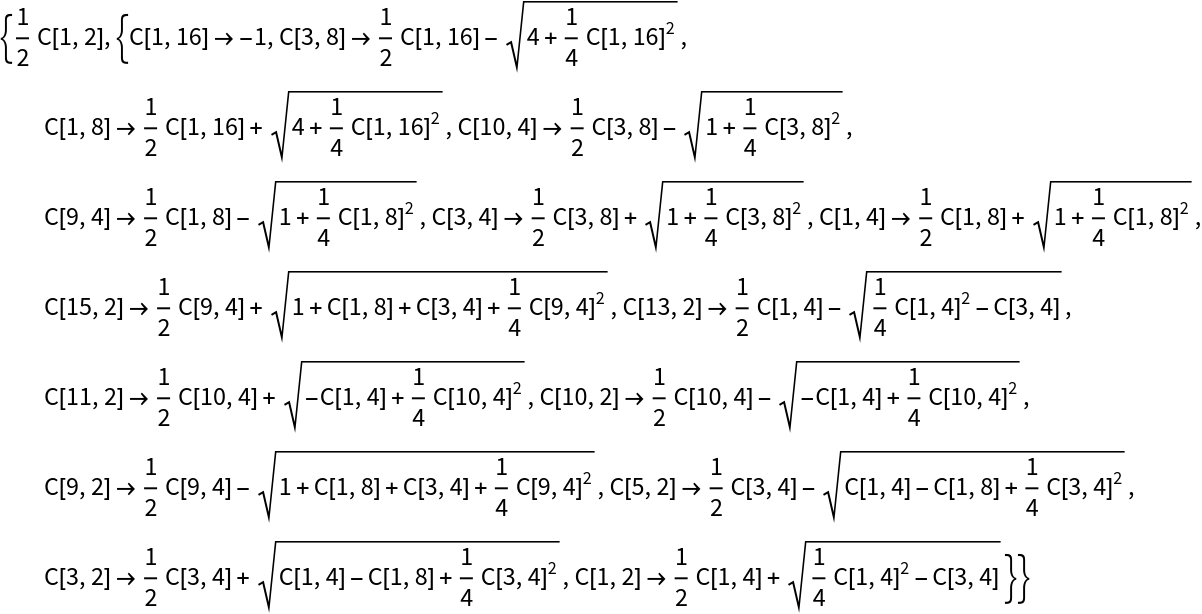
![(Rule @@@ Transpose[{(First /@ Last[cos17]), (Last /@ Last[cos17]) //. Last[cos17]}] // FullSimplify[#, ComplexityFunction -> (1000 Count[#, _Root, {0, \[Infinity]}] &)] &) // Column](https://www.wolframcloud.com/obj/resourcesystem/images/0ae/0aeaffc6-353f-492b-ae11-8603827eec75/0a1e51d66e2bd64b.png)