Function Repository Resource:

ConvexHullMeshGraphicsComplex

Source Notebook

Get a GraphicsComplex for ConvexHullMesh

Contributed by: Ed Pegg Jr

ResourceFunction["ConvexHullMeshGraphicsComplex"][pts]

returns the convex hull of pts in the GraphicsComplex format.

Examples

Basic Examples (2)

Return the GraphicsComplex of a square:

In[1]:=

Out[1]=

Show it:

In[2]:=

Out[2]=

Return the GraphicsComplex of a cube:

In[3]:=

Out[3]=

Show it:

In[4]:=

Out[4]=

Neat Examples (2)

Show the biggest known little polyhedron on 16 points with all unit length diagonals shown in red:

In[5]:=

$tetrahedralGroup = CompressedData[" 1:eJxTTMoPymNmYGDgAWJmKP4PBAxIAJ3PiEccXQyXODY+IwMqQFaDTQ6fPC4+ IXtx+RWXm3DZg08fOh/dL+j6sdmBLAYAQkFJkg== "]; partial16 = Join[# . {r, r, 1/2 Sqrt[1 - 4 r^2]} & /@ tetrahedralGroup, 1/6 (4 r + Sqrt[1 - 4 r^2] - Sqrt[10 + 8 r Sqrt[1 - 4 r^2]]) {{1, 1, 1}, {1, -1, -1}, {-1, 1, -1}, {-1, -1, 1}}] /. {r -> Root[ 71289 - 5627392 #^2 + 144921856 #^4 - 1690055680 #^6 + 9926729728 #^8 - 31050825728 #^10 + 55221420032 #^12 - 67570237440 #^14 + 58284048384 #^16& , 5, 0]}; diag = Select[Subsets[Range[16], {2}], Chop[(1 - ( EuclideanDistance @@ N[partial16[[#]]]))] == 0 &]; Graphics3D[{{Opacity[0.5], ResourceFunction["ConvexHullMeshGraphicsComplex"][ partial16]}, {Red, Tube[partial16[[#]]] & /@ diag}}, Boxed -> False, SphericalRegion -> True]$

Out[7]=

ConvexHullMesh also works in this case:

In[8]:=

Out[8]=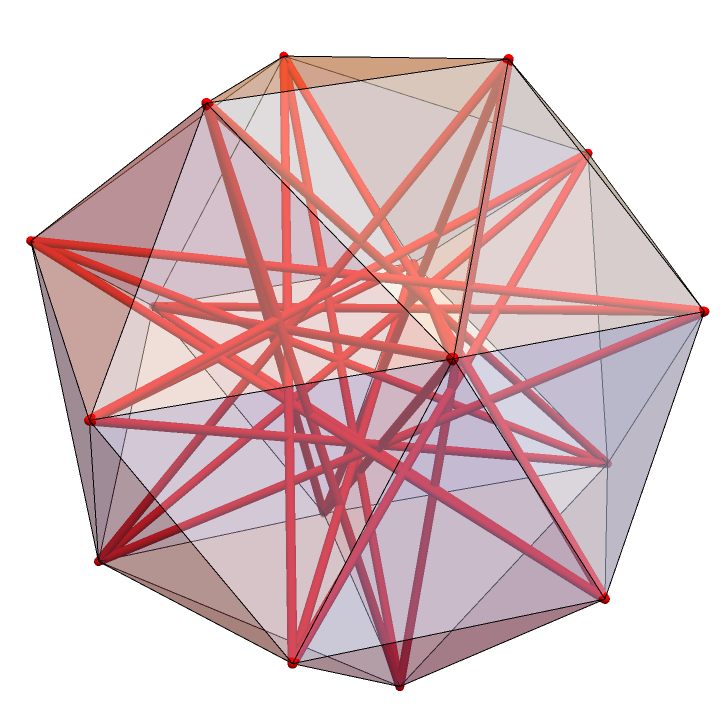

Version History

1.0.1 – 29 November 2022
1.0.0 – 28 November 2022

Related Resources

Author Notes

ConvexHullMesh[pts]["GraphicsComplex"] was deprecated in version 12. Said function option was used in many Wolfram Demonstrations, so this function is a fix for those.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License