Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ConsistentAugmentedMatrixQ

Source Notebook

Determine if a matrix represents a consistent system of linear equations

Contributed by: Peter Cullen Burbery

ResourceFunction["ConsistentAugmentedMatrixQ"][matrix]

returns True if matrix represents a consistent system of linear equations and returns False otherwise.

Details

The function uses MatrixRank and the coefficient matrix to verify the rank of the coefficient matrix equals the rank of the augmented matrix.
The input should be an augmented matrix representing a system of linear equations.
The function is based on the Rouchè-Capelli theorem.

Examples

Basic Examples

Determine if an augmented matrix represents a consistent linear system of equations:

In[1]:=
ResourceFunction["ConsistentAugmentedMatrixQ"][mat = ({ {1, 7, 3, -4}, {0, 1, -1, 3}, {0, 0, 0, 1}, {0, 0, 1, -2} })]
Out[1]=

The reduced row echelon form contains a contradiction that 0x1+0x2+0x3=1 so the matrix is not consistent:

In[2]:=
RowReduce[mat] // MatrixForm
Out[2]=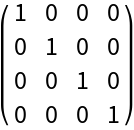

The solution set is empty. No solutions exist:

In[3]:=
LinearSolve[Map[Most][mat](*the coefficient matrix*), Map[Last][mat](*the right most column*)]
Out[3]=
In[4]:=
eqns = {Subscript[x, 1] + 7 Subscript[x, 2] + 3 Subscript[x, 3] == -4, Subscript[x, 2] - Subscript[x, 3] == 3, 0 Subscript[x, 1] + 0 Subscript[x, 2] + 0 Subscript[x, 3] == 1, Subscript[x, 3] == -2};
In[5]:=
Solve[eqns, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}]
Out[5]=

The following augmented matrix represents a consistent linear system:

In[6]:=
ResourceFunction["ConsistentAugmentedMatrixQ"][({ {1, 5, 2, -6}, {0, 4, -7, 2}, {0, 0, 5, 0} })]
Out[6]=

Publisher

Peter Burbery

Version History

  • 1.0.0 – 19 December 2022

Related Resources

License Information