Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate conditional and marginal distributions of the multivariate normal distribution
ResourceFunction["ConditionedMultinormalDistribution"][MultinormalDistribution[μ,Σ],i→xi] returns the MultinormalDistribution obtained by conditioning coordinate i to value xi. | |
ResourceFunction["ConditionedMultinormalDistribution"][…,{i1→xi1,i2→xi2,…}] conditions on multiple coordinates. | |
ResourceFunction["ConditionedMultinormalDistribution"][…,{i1,i2,…}→{xi1,xi2,…}] can also be used. | |
ResourceFunction["ConditionedMultinormalDistribution"][…,…,{n1,n2,…}] returns the marginal distributions of coordinates ni after conditioning. | |
ResourceFunction["ConditionedMultinormalDistribution"][Inactive[MultinormalDistribution][…],…] works with SparseArray and SymmetrizedArray objects. |
Condition a 2D symbolic multivariate normal distribution on the value of the second coordinate:
| In[1]:= |
| Out[2]= |
A NormalDistribution is returned if you specify that the first marginal should be computed:
| In[3]:= |
| Out[3]= |
Generate a random MultinormalDistribution:
| In[4]:= | ![randomDist = With[{dim = 10},
MultinormalDistribution[
RandomReal[{-10, 10}, dim],
RandomVariate[
InverseWishartMatrixDistribution[dim + 1, IdentityMatrix[dim]]]
]
];](https://www.wolframcloud.com/obj/resourcesystem/images/325/3250a8e9-b3ee-4318-9ed0-02fc665ed0fc/11027453546640a3.png) |
Calculate how the expected value of the second coordinate depends on the value of the first:
| In[5]:= |
| Out[5]= |
Calculate the derivative:
| In[6]:= |
| Out[6]= |
Condition on multiple indices and obtain the means of multiple marginals:
| In[7]:= |
| Out[7]= |
Generate some (x,y) data:
| In[8]:= |
| Out[9]= | 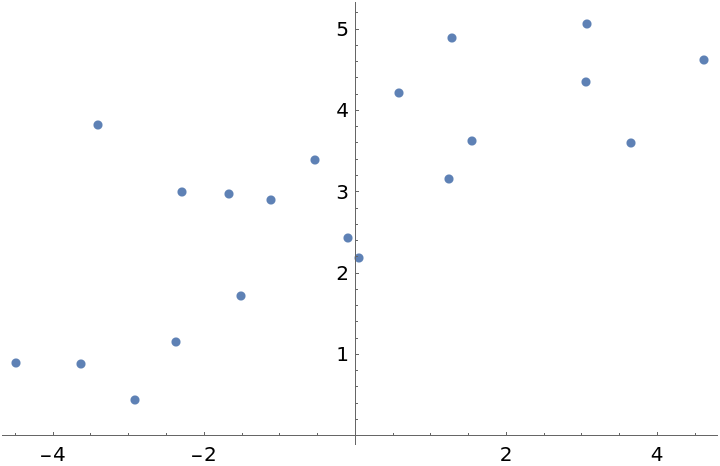 |
Perform a simple linear fit by estimating the joint distribution of the data and then condition it on x:
| In[10]:= | ![dist = Simplify@ResourceFunction["ConditionedMultinormalDistribution"][
EstimatedDistribution[data, MultinormalDistribution[{\[Mu]1, \[Mu]2}, {{\[CapitalSigma]11, \[CapitalSigma]12}, {\[CapitalSigma]12, \[CapitalSigma]22}}]],
1 -> \[FormalX],
2]](https://www.wolframcloud.com/obj/resourcesystem/images/325/3250a8e9-b3ee-4318-9ed0-02fc665ed0fc/7ff81c296459c9a6.png) |
| Out[10]= |
Plot the result:
| In[11]:= | ![Show[
Plot[Evaluate@InverseCDF[dist, {0.95, 0.5, 0.05}], {\[FormalX], -5, 5}, Filling -> {1 -> {3}}],
ListPlot[data]]](https://www.wolframcloud.com/obj/resourcesystem/images/325/3250a8e9-b3ee-4318-9ed0-02fc665ed0fc/7db63f04693bd05d.png) |
| Out[11]= | 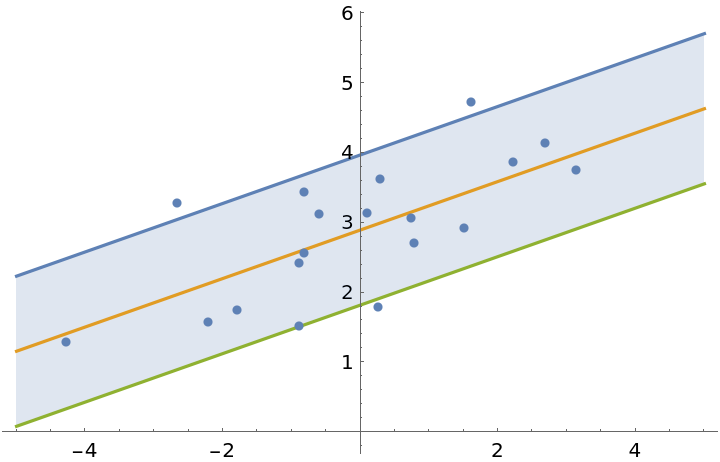 |
MultinormalDistribution normally converts SparseArray and StructuredArray objects to regular lists:
| In[12]:= |
| Out[13]= |  |
Use Inactive to keep the covariance matrix packed as a sparse array:
| In[14]:= | ![ResourceFunction["ConditionedMultinormalDistribution"][
Inactive[MultinormalDistribution][sparseCovariance],
1 -> 2
] // RepeatedTiming](https://www.wolframcloud.com/obj/resourcesystem/images/325/3250a8e9-b3ee-4318-9ed0-02fc665ed0fc/42d4ae29a8fd0431.png) |
| Out[14]= |
This is significantly more computationally efficient than having the covariance unpack into a regular list:
| In[15]:= | ![ResourceFunction["ConditionedMultinormalDistribution"][
MultinormalDistribution[sparseCovariance],
1 -> 2
] // RepeatedTiming](https://www.wolframcloud.com/obj/resourcesystem/images/325/3250a8e9-b3ee-4318-9ed0-02fc665ed0fc/197d7a8137382e8a.png) |
| Out[15]= |  |
Conditioning on variables can be done with Conditioned, but it is less convenient and results in a general ProbabilityDistribution:
| In[16]:= | ![dist1 = ProbabilityDistribution[
{
"CDF",
Simplify@Probability[
x1 < \[FormalY] \[Conditioned] x2 == a,
{x1, x2} \[Distributed] MultinormalDistribution[{\[Mu]1, \[Mu]2}, {{\[CapitalSigma]11, \[CapitalSigma]12}, {\[CapitalSigma]12, \[CapitalSigma]22}}]
]
},
{\[FormalY], -\[Infinity], \[Infinity]}
]](https://www.wolframcloud.com/obj/resourcesystem/images/325/3250a8e9-b3ee-4318-9ed0-02fc665ed0fc/3f159176f7cffc6d.png) |
| Out[16]= | 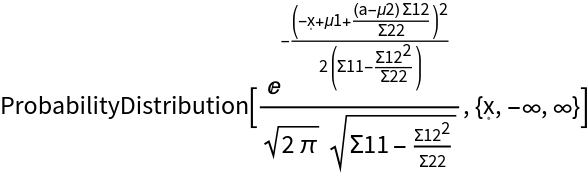 |
The same distribution with ConditionedMultinormalDistribution:
| In[17]:= | ![dist2 = Simplify@
ResourceFunction["ConditionedMultinormalDistribution"][
MultinormalDistribution[{\[Mu]1, \[Mu]2}, {{\[CapitalSigma]11, \[CapitalSigma]12}, {\[CapitalSigma]12, \[CapitalSigma]22}}], 2 -> a, 1]](https://www.wolframcloud.com/obj/resourcesystem/images/325/3250a8e9-b3ee-4318-9ed0-02fc665ed0fc/71f3cb4c8d461ba4.png) |
| Out[17]= |
The PDFs are the same up to a minus sign under the square:
| In[18]:= | ![{
PDF[dist1, x],
PDF[dist2, x]
}](https://www.wolframcloud.com/obj/resourcesystem/images/325/3250a8e9-b3ee-4318-9ed0-02fc665ed0fc/209198539daa3a4f.png) |
| Out[18]= | 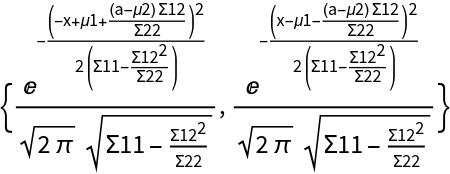 |
This work is licensed under a Creative Commons Attribution 4.0 International License