Function Repository Resource:

ConditionalProductDistribution

Represent a product of distributions where some distributions can depend on others

Contributed by: Sjoerd Smit

ResourceFunction["ConditionalProductDistribution"][Distributed[var₁,dist₁],Distributed[var₂,dist₂],…]

represents the multivariate distribution of {var₁,var₂, …} where each dist_i may depend on var_j for all i<j.

Details

ResourceFunction["ConditionalProductDistribution"] is used to define a multivariate distribution in terms of conditional probabilities using the conditional product rule

(where f_𝒟 denotes the PDF of a distribution 𝒟).

ResourceFunction["ConditionalProductDistribution"] is like a hybrid between ProductDistribution (which allows you to draw from multiple independent distributions at once) and ParameterMixtureDistribution (which allows you to define new distributions in terms of existing ones).

ResourceFunction["ConditionalProductDistribution"] works with RandomVariate, PDF, Likelihood and LogLikelihood and Mean. It does not necessarily work in all Wolfram Language functions for distributions.

Graph can be used to create a dependency graph of the variables var_i.

ResourceFunction["ConditionalProductDistribution"] will return $Failed if one of the dist_i depends on some var_j for i≥j.

Examples

Basic Examples (2)

Define a BinomialDistribution where the probability of success is drawn from a BetaDistribution:

In[1]:=

$dist = ResourceFunction[ "ConditionalProductDistribution"][\[FormalK] \[Distributed] BinomialDistribution[n, \[FormalP]], \[FormalP] \[Distributed] BetaDistribution[\[Alpha], \[Beta]]]$

Out[1]=

Compute the PDF:

In[2]:=

Out[2]=

Compute the Mean:

In[3]:=

Out[3]=

Draw random samples from the distribution. Each sample returns the values of k and p:

In[4]:=

$dist = ResourceFunction[ "ConditionalProductDistribution"][\[FormalK] \[Distributed] BinomialDistribution[10, \[FormalP]], \[FormalP] \[Distributed] BetaDistribution[2, 3]]; SeedRandom[1]; RandomVariate[dist]$

Out[5]=

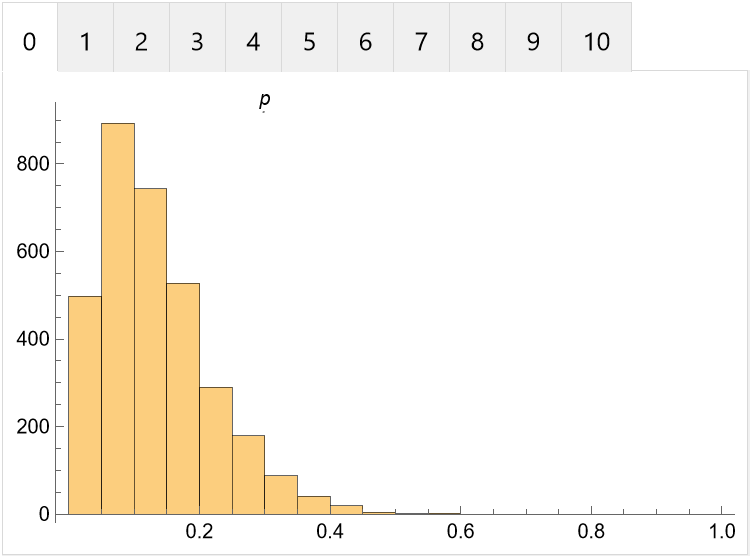
Generate multiple samples:

In[6]:=

Out[6]=

Calculate the LogLikelihood of the samples:

In[7]:=

Out[7]=

Samples with lower values of k are generally produced by samples with lower values of p:

In[8]:=

$TabView @ Map[ Histogram[#, {0.05}, PlotRange -> {{0, 1}, All}, ChartLabels -> {Placed[\[FormalP], Above]}] &, KeySort[GroupBy[RandomVariate[dist, 50000], First -> Last]] ]$

Out[8]=

Scope (2)

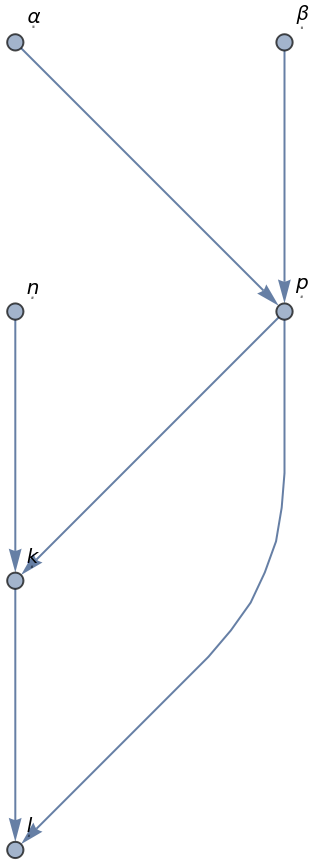
Graph can be used to generate a dependency graph of the individual random variables. Each edge x → y should be read as "x influences y":

In[9]:=

$dist = ResourceFunction["ConditionalProductDistribution"][ \[FormalL] \[Distributed] GeometricDistribution[\[FormalP]/(\[FormalK] + 1)], \[FormalK] \[Distributed] BinomialDistribution[\[FormalN], \[FormalP]], \[FormalP] \[Distributed] BetaDistribution[\[FormalAlpha] + 2, \[FormalBeta] + 2], {\[FormalN], \[FormalAlpha], \[FormalBeta]} \[Distributed] ProductDistribution[{GeometricDistribution[1/10], 3}] ]; Graph[dist]$

Out[10]=

The graph is acyclic:

In[11]:=

Out[11]=

Sample the distribution and compute the expected value. Note that the coordinates are listed in order of appearance of the symbols:

In[12]:=

Out[12]=

In[13]:=

Out[13]=

In[14]:=

Out[14]=

When a ConditionalProductDistribution is defined using unprotected symbols for the bound variables, they will be replaced with symbols of the form x[i]:

In[15]:=

$ResourceFunction["ConditionalProductDistribution"][ k \[Distributed] BinomialDistribution[10, p], p \[Distributed] BetaDistribution[2, 3]]$

Out[15]=

Applications (3)

Define a Normal-inverse-Wishart distribution, which is the conjugate prior to a multivariate normal distribution of unknown mean and covariance:

In[16]:=

$normalInverseWishartDistribution[\[Mu]0_, \[Lambda]_, \[CapitalPsi]_, \[Nu]_] := ResourceFunction["ConditionalProductDistribution"][ \[FormalMu] \[Distributed] MultinormalDistribution[\[Mu]0, \[FormalCapitalSigma]/\[Lambda]], \[FormalCapitalSigma] \[Distributed] InverseWishartMatrixDistribution[\[Nu], \[CapitalPsi]] ];$

Draw samples from it:

In[17]:=

Out[17]=

Draw samples from the posterior predictive distribution:

In[18]:=

$posteriorPredictiveDistribution[\[Mu]0_, \[Lambda]_, \[CapitalPsi]_, \[Nu]_] := ResourceFunction["ConditionalProductDistribution"][ \[FormalCapitalX] \[Distributed] MultinormalDistribution[\[Mu], \[CapitalSigma]], {\[Mu], \[CapitalSigma]} \[Distributed] normalInverseWishartDistribution[\[Mu]0, \[Lambda], \[CapitalPsi], \[Nu]] ]; RandomVariate[posteriorPredictiveDistribution[{1, -3}, 5, ( { {1, 1/2}, {1/2, 2} } ), 7], 5]$

Out[12]=

Properties and Relations (3)

A ParameterMixtureDistribution is the marginal distribution of a ConditionalProductDistribution:

In[19]:=

$pdf1 = PDF[ ParameterMixtureDistribution[BinomialDistribution[n, p], p \[Distributed] BetaDistribution[\[Alpha], \[Beta]]], k]$

Out[19]=

Compute the marginal over k by integrating out p from the PDF of the corresponding ConditionalProductDistribution:

In[20]:=

$pdf2 = Simplify@Integrate[ PDF[ResourceFunction[ "ConditionalProductDistribution"][\[FormalK] \[Distributed] BinomialDistribution[n, p], \[FormalP] \[Distributed] BetaDistribution[\[Alpha], \[Beta]]], {k, p}], {p, 0, 1} ]$

Out[20]=

The result is the same:

In[21]:=

Out[21]=

Possible Issues (3)

The distributions need to be ordered correctly and cannot be circular:

In[22]:=

$ResourceFunction[ "ConditionalProductDistribution"][\[FormalP] \[Distributed] BetaDistribution[1, 2], \[FormalK] \[Distributed] BinomialDistribution[10, \[FormalP]]]$

Out[22]=

In[23]:=

$ResourceFunction[ "ConditionalProductDistribution"][\[FormalK] \[Distributed] BinomialDistribution[\[FormalK], \[FormalP]]]$

Out[23]=

In some cases PDF cannot distinguish between evaluating a single coordinate or threading over multiple coordinates. In the following example, the second argument will be interpreted as a pair of coordinates rather than a single 2×2 coordinate:

In[24]:=

$PDF[ ResourceFunction["ConditionalProductDistribution"][ \[FormalX] \[Distributed] ProductDistribution[{NormalDistribution[Indexed[\[FormalY], 1], Indexed[\[FormalY], 2]^2], 2}], \[FormalY] \[Distributed] ProductDistribution[{NormalDistribution[], 2}] ], {{1, 2}, {3, 4}}]$

Out[24]=

In this case, wrap the second argument in a list to remove the ambiguity:

In[25]:=

Out[25]=

Bound variables should not have definitions at the time of defining a ConditionalProductDistribution, since this can have unexpected results:

In[26]:=

$p = 10; dist = ResourceFunction[ "ConditionalProductDistribution"][\[FormalK] \[Distributed] BinomialDistribution[10, p], p \[Distributed] BetaDistribution[2, 3]]$

Out[27]=

In[28]:=

Out[28]=

Use Clear or Block to make sure p has no value at the moment of definition. After that, the variable will have been localized so that p can be used again:

In[29]:=

$Block[{p}, dist = ResourceFunction[ "ConditionalProductDistribution"][\[FormalK] \[Distributed] BinomialDistribution[10, p], p \[Distributed] BetaDistribution[2, 3]] ]$

Out[29]=

In[30]:=

Out[31]=

Neat Examples (3)

Define a function that can compute the Expectation of a ConditionalProductDistribution:

In[32]:=

conditionalExpectation[expr_, dist_] := Fold[
Expectation[#1, #2] &,
expr,
List @@ dist
];

Define a distribution using formal symbols (to ensure they do not get renamed) and compute an expected value:

In[33]:=

$dist = ResourceFunction[ "ConditionalProductDistribution"][\[FormalK] \[Distributed] BinomialDistribution[n, \[FormalP]], \[FormalP] \[Distributed] BetaDistribution[\[Alpha], \[Beta]]]; conditionalExpectation[\[FormalP]*\[FormalK]^2, dist]$