Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Condense a graph by contracting strongly connected components
ResourceFunction["CondenseGraph"][gr] contracts each strongly connected component of a directed graph gr into a single vertex. |
Vertices 1, 2 and 3 of this graph are strongly connected and are replaced with a single vertex in the condensation graph:
| In[1]:= | ![ResourceFunction["CondenseGraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4}, {{{1, 2}, {2, 3}, {3, 1}, {3, 4}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{{0.00010588781145626225`, 0.}, {0., 0.8477985637290937}}, {{0., 0.8477985637290937}, {
0.9160505679059736, 0.4239474668844526}}, {{
0.9160505679059736, 0.4239474668844526}, {
0.00010588781145626225`, 0.}}, {{0.9160505679059736, 0.4239474668844526}, {2.031287348500572, 0.42392728771489974`}}}, 0.022864823094682685`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{0.00010588781145626225`, 0.}, 0.022864823094682685], InsetBox["1", Offset[{2, 2}, {0.022970710906138947, 0.022864823094682685}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.8477985637290937}, 0.022864823094682685], InsetBox["2", Offset[{2, 2}, {0.022864823094682685, 0.8706633868237763}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.9160505679059736, 0.4239474668844526}, 0.022864823094682685], InsetBox["3", Offset[{2, 2}, {0.9389153910006562, 0.4468122899791353}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.031287348500572, 0.42392728771489974`}, 0.022864823094682685], InsetBox["4", Offset[{2, 2}, {2.0541521715952547, 0.4467921108095824}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{182.3828125, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4494fc13-a38d-4f43-9de3-e5c0db6a6e8c/39d0eea56fe76add.png) |
| Out[1]= |
Each separate strongly connected subgraph is replaced with a different vertex:
| In[2]:= | ![ResourceFunction["CondenseGraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{"a", "b", "c", "d", "e", "f", "g", "h"}, {{{1, 2}, {2, 3}, {3, 4}, {4, 3}, {2, 5}, {2, 6}, {5, 1}, {1, 6}, {6, 7}, {7, 6}, {
3, 7}, {4, 8}, {8, 4}, {8, 7}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{3.1357578517568445`, 0.24015430469611865`}, {
2.521629950017237, 0.7825840134172464}}, 0.03400933871162268], ArrowBox[{{3.1357578517568445`, 0.24015430469611865`}, {
2.1872984513036924`, 0.}}, 0.03400933871162268], ArrowBox[{{2.521629950017237, 0.7825840134172464}, {
1.281110940442222, 0.9504436011965234}}, 0.03400933871162268], ArrowBox[{{2.521629950017237, 0.7825840134172464}, {
3.5427674589041027`, 0.9150200944157839}}, 0.03400933871162268], ArrowBox[{{2.521629950017237, 0.7825840134172464}, {
2.1872984513036924`, 0.}}, 0.03400933871162268], ArrowBox[
BezierCurveBox[{{1.281110940442222, 0.9504436011965234}, {
0.7194614939198618, 0.8404007931432466}, {
0.2021352490745234, 1.0852131228518151`}}], 0.03400933871162268], ArrowBox[{{1.281110940442222, 0.9504436011965234}, {
1.040696687656542, 0.08700290601849842}}, 0.03400933871162268], ArrowBox[
BezierCurveBox[{{0.2021352490745234, 1.0852131228518151`}, {0.7637846955968882, 1.1952559309050945`}, {1.281110940442222, 0.9504436011965234}}], 0.03400933871162268], ArrowBox[
BezierCurveBox[{{0.2021352490745234, 1.0852131228518151`}, {0.23839256196018188`, 0.6344224240471941}, {0., 0.2501102680222931}}], 0.03400933871162268], ArrowBox[{{3.5427674589041027`, 0.9150200944157839}, {
3.1357578517568445`, 0.24015430469611865`}}, 0.03400933871162268], ArrowBox[
BezierCurveBox[{{2.1872984513036924`, 0.}, {
1.5996907466073362`, -0.14504659772636677`}, {
1.040696687656542, 0.08700290601849842}}], 0.03400933871162268], ArrowBox[ BezierCurveBox[{{1.040696687656542, 0.08700290601849842}, {
1.6283043923529021`, 0.23204950374486524`}, {
2.1872984513036924`, 0.}}], 0.03400933871162268], ArrowBox[
BezierCurveBox[{{0., 0.2501102680222931}, {-0.0362573128856584, 0.7009009668269116}, {0.2021352490745234, 1.0852131228518151`}}], 0.03400933871162268], ArrowBox[{{0., 0.2501102680222931}, {1.040696687656542, 0.08700290601849842}}, 0.03400933871162268]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{3.1357578517568445`, 0.24015430469611865`}, 0.03400933871162268], InsetBox["\<\"a\"\>", Offset[{2, 2}, {3.169767190468467, 0.27416364340774135}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.521629950017237, 0.7825840134172464}, 0.03400933871162268], InsetBox["\<\"b\"\>", Offset[{2, 2}, {2.5556392887288597, 0.8165933521288691}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.281110940442222, 0.9504436011965234}, 0.03400933871162268], InsetBox["\<\"c\"\>", Offset[{2, 2}, {1.3151202791538448, 0.9844529399081461}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.2021352490745234, 1.0852131228518151`}, 0.03400933871162268], InsetBox["\<\"d\"\>", Offset[{2, 2}, {0.23614458778614608, 1.1192224615634379}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.5427674589041027`, 0.9150200944157839}, 0.03400933871162268], InsetBox["\<\"e\"\>", Offset[{2, 2}, {3.576776797615725, 0.9490294331274066}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.1872984513036924`, 0.}, 0.03400933871162268], InsetBox["\<\"f\"\>", Offset[{2, 2}, {2.221307790015315, 0.03400933871162268}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.040696687656542, 0.08700290601849842}, 0.03400933871162268], InsetBox["\<\"g\"\>", Offset[{2, 2}, {1.0747060263681647, 0.1210122447301211}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.2501102680222931}, 0.03400933871162268], InsetBox["\<\"h\"\>", Offset[{2, 2}, {0.03400933871162268, 0.2841196067339158}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{226.1875, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4494fc13-a38d-4f43-9de3-e5c0db6a6e8c/31aad093389f97e5.png) |
| Out[2]= | 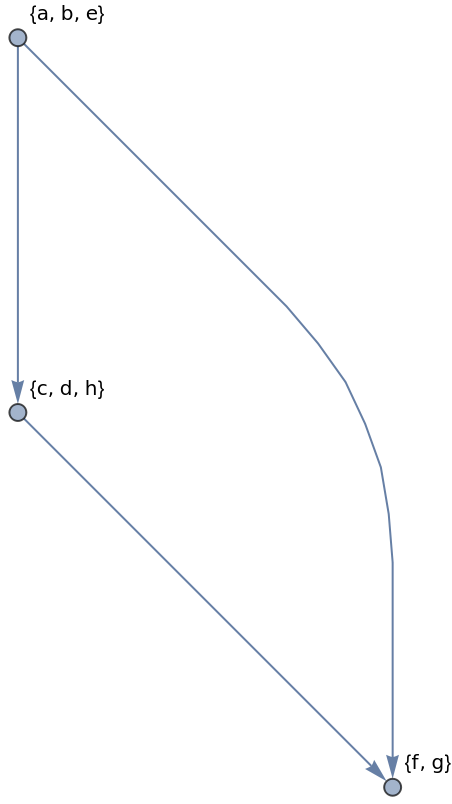 |
Self-loops are included in the new vertex:
| In[3]:= | ![ResourceFunction["CondenseGraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 3, 2, 5, 4, 12, 13, 6, 8, 7, 10, 9, 11, 14, 15}, {{{1, 1}, {1, 2}, {3, 1}, {2, 3}, {2, 4}, {5, 1}, {5, 3}, {5, 6}, {5, 7}, {4, 8}, {4, 9}, {8, 10}, {8, 9}, {8, 11}, {10, 11}, {9, 12}, {9, 11}, {12, 4}, {12, 13}, {11, 12}, {11, 13}, {11, 14}, {13, 6}, {13, 14}, {6, 7}, {7, 13}, {7, 15}, {14, 7}, {15, 14}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[
BezierCurveBox[{{0.3917483376919404, 0.5614086844084661}, {
0.531936229791304, 0.28300446393806505`}, {
0.4752258448896619, 0.14665293844113045`}, {
0.39368553557489194`, 0.08960825056285282}, {
0.12728292514122616`, 0.17069466152609353`}, {
0.09135170003060133, 0.26349479902775935`}, {
0.1202244285944419, 0.40831942333699894`}, {
0.3917483376919404, 0.5614086844084661}},
SplineDegree->7], 0.03908097173246734], ArrowBox[{{0.3917483376919404, 0.5614086844084661}, {
1.0374624367030891`, 0.}}, 0.03908097173246734], ArrowBox[{{1.0374624367030891`, 0.}, {0., 0.5122872702298756}}, 0.03908097173246734], ArrowBox[{{1.0374624367030891`, 0.}, {2.4872641722031603`, 0.11997760009202785`}}, 0.03908097173246734], ArrowBox[{{0., 0.5122872702298756}, {0.3917483376919404, 0.5614086844084661}}, 0.03908097173246734], ArrowBox[{{2.4872641722031603`, 0.11997760009202785`}, {
3.6829422097580773`, 0.5519027464626287}}, 0.03908097173246734], ArrowBox[{{2.4872641722031603`, 0.11997760009202785`}, {
3.1890153315200447`, 0.47092225666092435`}}, 0.03908097173246734], ArrowBox[{{0.5170648035738898, 1.5497282181274306`}, {
0.3917483376919404, 0.5614086844084661}}, 0.03908097173246734], ArrowBox[{{0.5170648035738898, 1.5497282181274306`}, {0., 0.5122872702298756}}, 0.03908097173246734], ArrowBox[{{0.5170648035738898, 1.5497282181274306`}, {
1.1051369477286328`, 2.1540998372516564`}}, 0.03908097173246734], ArrowBox[{{0.5170648035738898, 1.5497282181274306`}, {
1.5397010203070338`, 2.535428284203424}}, 0.03908097173246734], ArrowBox[{{1.1051369477286328`, 2.1540998372516564`}, {
1.5397010203070338`, 2.535428284203424}}, 0.03908097173246734], ArrowBox[{{1.5397010203070338`, 2.535428284203424}, {
2.2441540746428585`, 1.9420740873153703`}}, 0.03908097173246734], ArrowBox[{{1.5397010203070338`, 2.535428284203424}, {
2.0355600435931027`, 3.4179025912863095`}}, 0.03908097173246734], ArrowBox[{{3.6829422097580773`, 0.5519027464626287}, {
3.1890153315200447`, 0.47092225666092435`}}, 0.03908097173246734], ArrowBox[{{3.6829422097580773`, 0.5519027464626287}, {
4.331171307920883, 1.1256625610127522`}}, 0.03908097173246734], ArrowBox[{{3.6829422097580773`, 0.5519027464626287}, {
3.277897662581644, 1.474532461167784}}, 0.03908097173246734], ArrowBox[{{3.1890153315200447`, 0.47092225666092435`}, {
3.277897662581644, 1.474532461167784}}, 0.03908097173246734], ArrowBox[{{3.1890153315200447`, 0.47092225666092435`}, {
2.7112326951644814`, 0.9942850072708016}}, 0.03908097173246734], ArrowBox[{{4.331171307920883, 1.1256625610127522`}, {
3.277897662581644, 1.474532461167784}}, 0.03908097173246734], ArrowBox[{{3.277897662581644, 1.474532461167784}, {
2.7112326951644814`, 0.9942850072708016}}, 0.03908097173246734], ArrowBox[{{3.277897662581644, 1.474532461167784}, {
2.2441540746428585`, 1.9420740873153703`}}, 0.03908097173246734], ArrowBox[{{3.277897662581644, 1.474532461167784}, {
2.5508329251072315`, 2.597095520261269}}, 0.03908097173246734], ArrowBox[{{2.7112326951644814`, 0.9942850072708016}, {
2.4872641722031603`, 0.11997760009202785`}}, 0.03908097173246734], ArrowBox[{{2.7112326951644814`, 0.9942850072708016}, {
2.2441540746428585`, 1.9420740873153703`}}, 0.03908097173246734], ArrowBox[{{2.2441540746428585`, 1.9420740873153703`}, {
1.1051369477286328`, 2.1540998372516564`}}, 0.03908097173246734], ArrowBox[{{2.2441540746428585`, 1.9420740873153703`}, {
2.5508329251072315`, 2.597095520261269}}, 0.03908097173246734], ArrowBox[{{2.5508329251072315`, 2.597095520261269}, {
1.5397010203070338`, 2.535428284203424}}, 0.03908097173246734], ArrowBox[{{2.0355600435931027`, 3.4179025912863095`}, {
2.5508329251072315`, 2.597095520261269}}, 0.03908097173246734]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{0.3917483376919404, 0.5614086844084661}, 0.03908097173246734], InsetBox["1", Offset[{2, 2}, {0.4308293094244077, 0.6004896561409335}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.0374624367030891`, 0.}, 0.03908097173246734], InsetBox["3", Offset[{2, 2}, {1.0765434084355565, 0.03908097173246734}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.5122872702298756}, 0.03908097173246734], InsetBox["2", Offset[{2, 2}, {0.03908097173246734, 0.551368241962343}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.4872641722031603`, 0.11997760009202785`}, 0.03908097173246734], InsetBox["5", Offset[{2, 2}, {2.5263451439356275, 0.15905857182449518}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.5170648035738898, 1.5497282181274306`}, 0.03908097173246734], InsetBox["4", Offset[{2, 2}, {0.5561457753063572, 1.588809189859898}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.1051369477286328`, 2.1540998372516564`}, 0.03908097173246734], InsetBox["12", Offset[{2, 2}, {1.1442179194611002, 2.1931808089841236}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.5397010203070338`, 2.535428284203424}, 0.03908097173246734], InsetBox["13", Offset[{2, 2}, {1.5787819920395012, 2.574509255935891}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.6829422097580773`, 0.5519027464626287}, 0.03908097173246734], InsetBox["6", Offset[{2, 2}, {3.7220231814905445, 0.5909837181950961}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.1890153315200447`, 0.47092225666092435`}, 0.03908097173246734], InsetBox["8", Offset[{2, 2}, {3.228096303252512, 0.5100032283933917}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{4.331171307920883, 1.1256625610127522`}, 0.03908097173246734], InsetBox["7", Offset[{2, 2}, {4.37025227965335, 1.1647435327452196}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.277897662581644, 1.474532461167784}, 0.03908097173246734], InsetBox["10", Offset[{2, 2}, {3.316978634314111, 1.5136134329002513}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.7112326951644814`, 0.9942850072708016}, 0.03908097173246734], InsetBox["9", Offset[{2, 2}, {2.7503136668969486, 1.033365979003269}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.2441540746428585`, 1.9420740873153703`}, 0.03908097173246734], InsetBox["11", Offset[{2, 2}, {2.2832350463753257, 1.9811550590478377}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.5508329251072315`, 2.597095520261269}, 0.03908097173246734], InsetBox["14", Offset[{2, 2}, {2.5899138968396986, 2.6361764919937363}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.0355600435931027`, 3.4179025912863095`}, 0.03908097173246734], InsetBox["15", Offset[{2, 2}, {2.07464101532557, 3.4569835630187766}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{362.078125, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4494fc13-a38d-4f43-9de3-e5c0db6a6e8c/6d68a4849e3043bc.png) |
| Out[3]= | 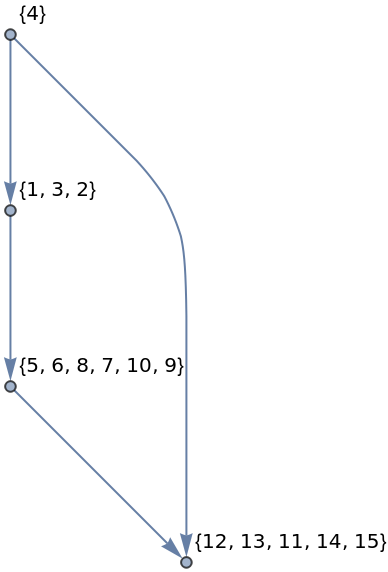 |
Disconnected components remain disconnected:
| In[4]:= | ![ResourceFunction["CondenseGraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6}, {{{1, 2}, {2, 3}, {3, 1}, {4, 5}, {5, 6}, {6, 4}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{{0.2342364699455688, -0.2342364699455688}, {
0.720269132659022, -1.1081770670971065`}}, {{
0.720269132659022, -1.1081770670971065`}, {
1.2341076323585818`, -0.25029011729888495`}}, {{
1.2341076323585818`, -0.25029011729888495`}, {
0.2342364699455688, -0.2342364699455688}}, {{
0.2342364699455688, -1.576650006988244}, {
0.720269132659022, -2.450590604139782}}, {{
0.720269132659022, -2.450590604139782}, {
1.2341076323585818`, -1.5927036543415602`}}, {{
1.2341076323585818`, -1.5927036543415602`}, {
0.2342364699455688, -1.576650006988244}}}, 0.024343082395781784`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{0.2342364699455688, -0.2342364699455688}, 0.024343082395781784], InsetBox["1", Offset[{2, 2}, {0.25857955234135055, -0.209893387549787}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.720269132659022, -1.1081770670971065`}, 0.024343082395781784], InsetBox["2", Offset[{2, 2}, {0.7446122150548038, -1.0838339847013247}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.2341076323585818`, -0.25029011729888495`}, 0.024343082395781784], InsetBox["3", Offset[{2, 2}, {1.2584507147543635, -0.22594703490310317}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.2342364699455688, -1.576650006988244}, 0.024343082395781784], InsetBox["4", Offset[{2, 2}, {0.25857955234135055, -1.5523069245924623}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.720269132659022, -2.450590604139782}, 0.024343082395781784], InsetBox["5", Offset[{2, 2}, {0.7446122150548038, -2.426247521744}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.2341076323585818`, -1.5927036543415602`}, 0.024343082395781784], InsetBox["6", Offset[{2, 2}, {1.2584507147543635, -1.5683605719457785}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{90.89726454604948, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4494fc13-a38d-4f43-9de3-e5c0db6a6e8c/7655b8212cf1a95b.png) |
| Out[4]= |
Graph condensation discards undirected edges. Condensing an undirected graph will result in disconnected vertices:
| In[5]:= |
| Out[5]= |  |
| In[6]:= |
| Out[6]= |  |
A condensation graph is acyclic:
| In[7]:= | ![gr = ResourceFunction["CondenseGraph"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{"a", "b", "c", "d", "e", "f", "g", "h"}, {{{1, 2}, {2, 3}, {3, 4}, {4, 3}, {2, 5}, {2, 6}, {5, 1}, {1, 6}, {6, 7}, {7, 6}, {3, 7}, {4, 8}, {8, 4}, {8, 7}}, Null}, {VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{3.1357578517568445`, 0.24015430469611865`}, {
2.521629950017237, 0.7825840134172464}}, 0.03400933871162268], ArrowBox[{{3.1357578517568445`, 0.24015430469611865`}, {
2.1872984513036924`, 0.}}, 0.03400933871162268], ArrowBox[{{2.521629950017237, 0.7825840134172464}, {
1.281110940442222, 0.9504436011965234}}, 0.03400933871162268], ArrowBox[{{2.521629950017237, 0.7825840134172464}, {
3.5427674589041027`, 0.9150200944157839}}, 0.03400933871162268], ArrowBox[{{2.521629950017237, 0.7825840134172464}, {
2.1872984513036924`, 0.}}, 0.03400933871162268], ArrowBox[
BezierCurveBox[{{1.281110940442222, 0.9504436011965234}, {
0.7194614939198618, 0.8404007931432466}, {
0.2021352490745234, 1.0852131228518151`}}], 0.03400933871162268], ArrowBox[{{1.281110940442222, 0.9504436011965234}, {
1.040696687656542, 0.08700290601849842}}, 0.03400933871162268], ArrowBox[
BezierCurveBox[{{0.2021352490745234, 1.0852131228518151`}, {0.7637846955968882, 1.1952559309050945`}, {1.281110940442222, 0.9504436011965234}}], 0.03400933871162268], ArrowBox[
BezierCurveBox[{{0.2021352490745234, 1.0852131228518151`}, {0.23839256196018188`, 0.6344224240471941}, {0., 0.2501102680222931}}], 0.03400933871162268], ArrowBox[{{3.5427674589041027`, 0.9150200944157839}, {
3.1357578517568445`, 0.24015430469611865`}}, 0.03400933871162268], ArrowBox[
BezierCurveBox[{{2.1872984513036924`, 0.}, {
1.5996907466073362`, -0.14504659772636677`}, {
1.040696687656542, 0.08700290601849842}}], 0.03400933871162268], ArrowBox[
BezierCurveBox[{{1.040696687656542, 0.08700290601849842}, {1.6283043923529021`, 0.23204950374486524`}, {2.1872984513036924`, 0.}}], 0.03400933871162268], ArrowBox[
BezierCurveBox[{{0., 0.2501102680222931}, {-0.0362573128856584, 0.7009009668269116}, {0.2021352490745234, 1.0852131228518151`}}], 0.03400933871162268], ArrowBox[{{0., 0.2501102680222931}, {1.040696687656542, 0.08700290601849842}}, 0.03400933871162268]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{3.1357578517568445`, 0.24015430469611865`}, 0.03400933871162268], InsetBox["\<\"a\"\>", Offset[{2, 2}, {3.169767190468467, 0.27416364340774135}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.521629950017237, 0.7825840134172464}, 0.03400933871162268], InsetBox["\<\"b\"\>", Offset[{2, 2}, {2.5556392887288597, 0.8165933521288691}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.281110940442222, 0.9504436011965234}, 0.03400933871162268], InsetBox["\<\"c\"\>", Offset[{2, 2}, {1.3151202791538448, 0.9844529399081461}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.2021352490745234, 1.0852131228518151`}, 0.03400933871162268], InsetBox["\<\"d\"\>", Offset[{2, 2}, {0.23614458778614608, 1.1192224615634379}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.5427674589041027`, 0.9150200944157839}, 0.03400933871162268], InsetBox["\<\"e\"\>", Offset[{2, 2}, {3.576776797615725, 0.9490294331274066}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.1872984513036924`, 0.}, 0.03400933871162268], InsetBox["\<\"f\"\>", Offset[{2, 2}, {2.221307790015315, 0.03400933871162268}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.040696687656542, 0.08700290601849842}, 0.03400933871162268], InsetBox["\<\"g\"\>", Offset[{2, 2}, {1.0747060263681647, 0.1210122447301211}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0., 0.2501102680222931}, 0.03400933871162268], InsetBox["\<\"h\"\>", Offset[{2, 2}, {0.03400933871162268, 0.2841196067339158}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->"NetworkGraphics",
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{210.52734375, Automatic}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/449/4494fc13-a38d-4f43-9de3-e5c0db6a6e8c/57e93fff10d322c6.png) |
| Out[7]= | 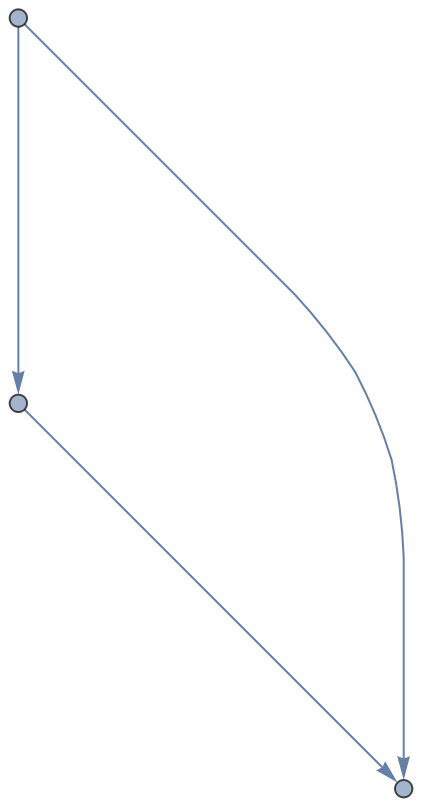 |
| In[8]:= |
| Out[8]= |
A directed graph is acyclic, if and only if its condensation is isomorphic to itself:
| In[9]:= |
| Out[9]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License