Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the complete k-ary tree with different amounts of branches per level
ResourceFunction["CompleteLevelsKaryTree"][{n1,n2,n3,…}] gives the complete k-ary tree with ni branches at level i. |
Create a k-ary tree with two branches on the top level, three branches in the level below, and four in the bottom level:
| In[1]:= |
| Out[1]= |  |
There can be one branch for a certain level:
| In[2]:= |
| Out[2]= | 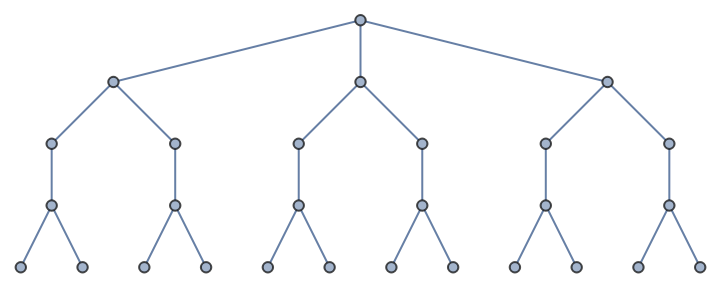 |
Use directed edges:
| In[3]:= |
| Out[3]= | 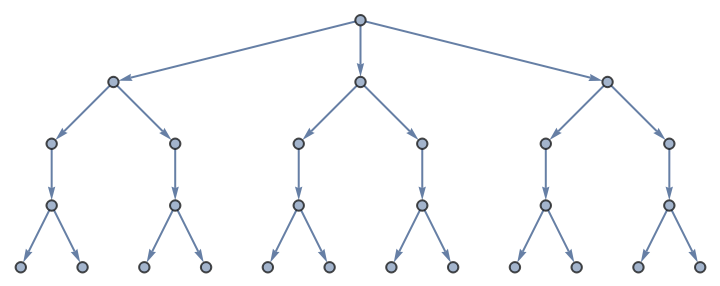 |
By default, an undirected graph is generated:
| In[4]:= |
| Out[4]= | 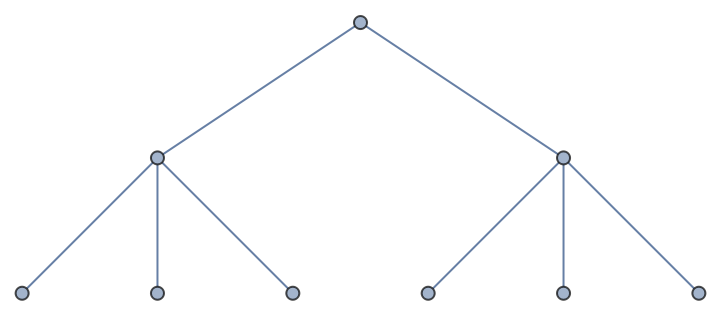 |
Use DirectedEdges → True to generate a directed graph:
| In[5]:= |
| Out[5]= | 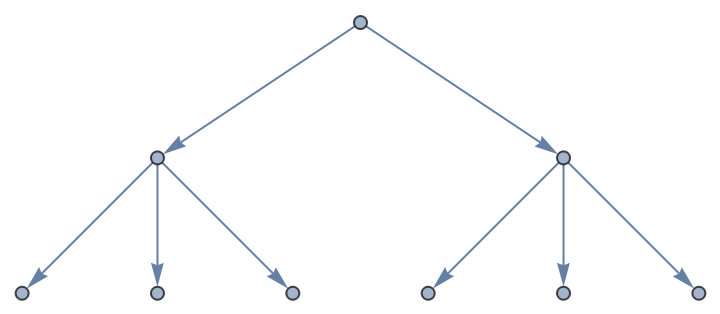 |
CompleteKaryTree and CompleteLevelsKaryTree can be the same:
| In[6]:= |
| Out[6]= | 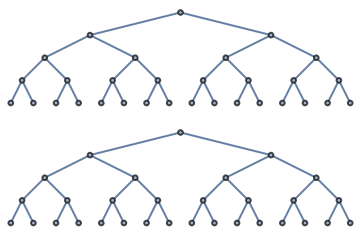 |
If a zero is present the branching is stopped:
| In[7]:= |
| Out[7]= | 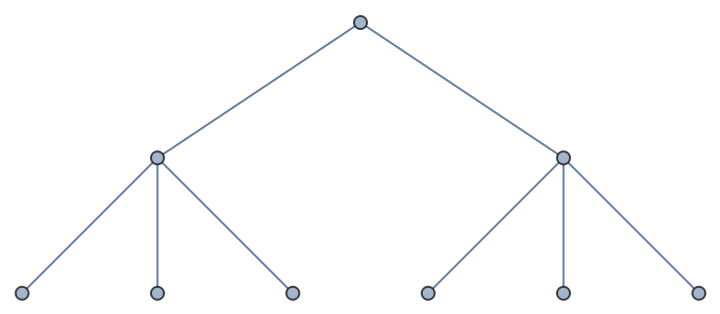 |
Here is a complete k-ary tree:
| In[8]:= |
| Out[8]= | 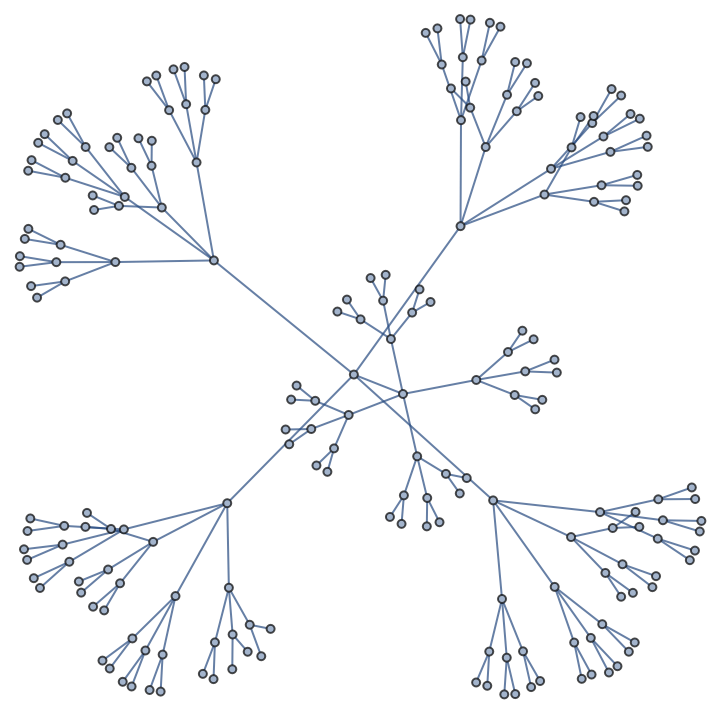 |
Using the radial embedding emphasizes the symmetry:
| In[9]:= |
| Out[9]= | 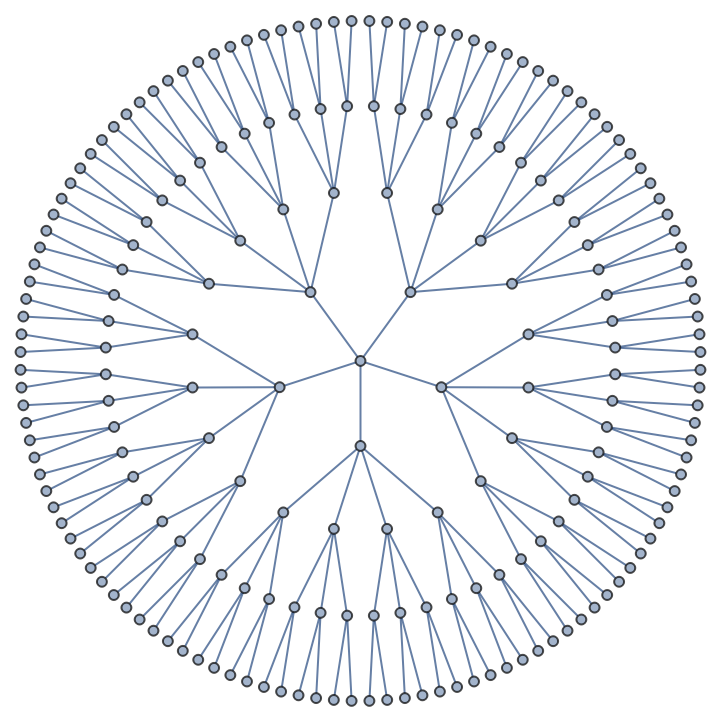 |
This work is licensed under a Creative Commons Attribution 4.0 International License