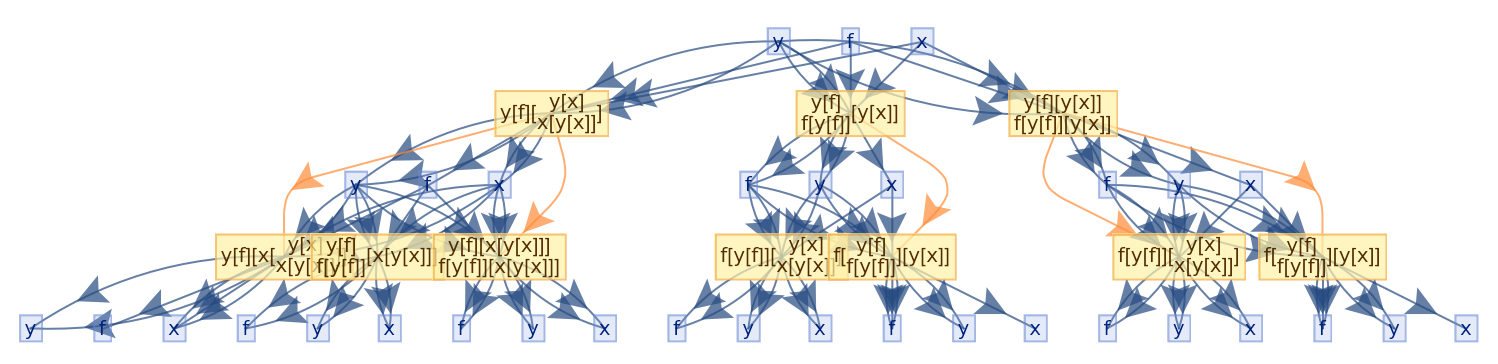
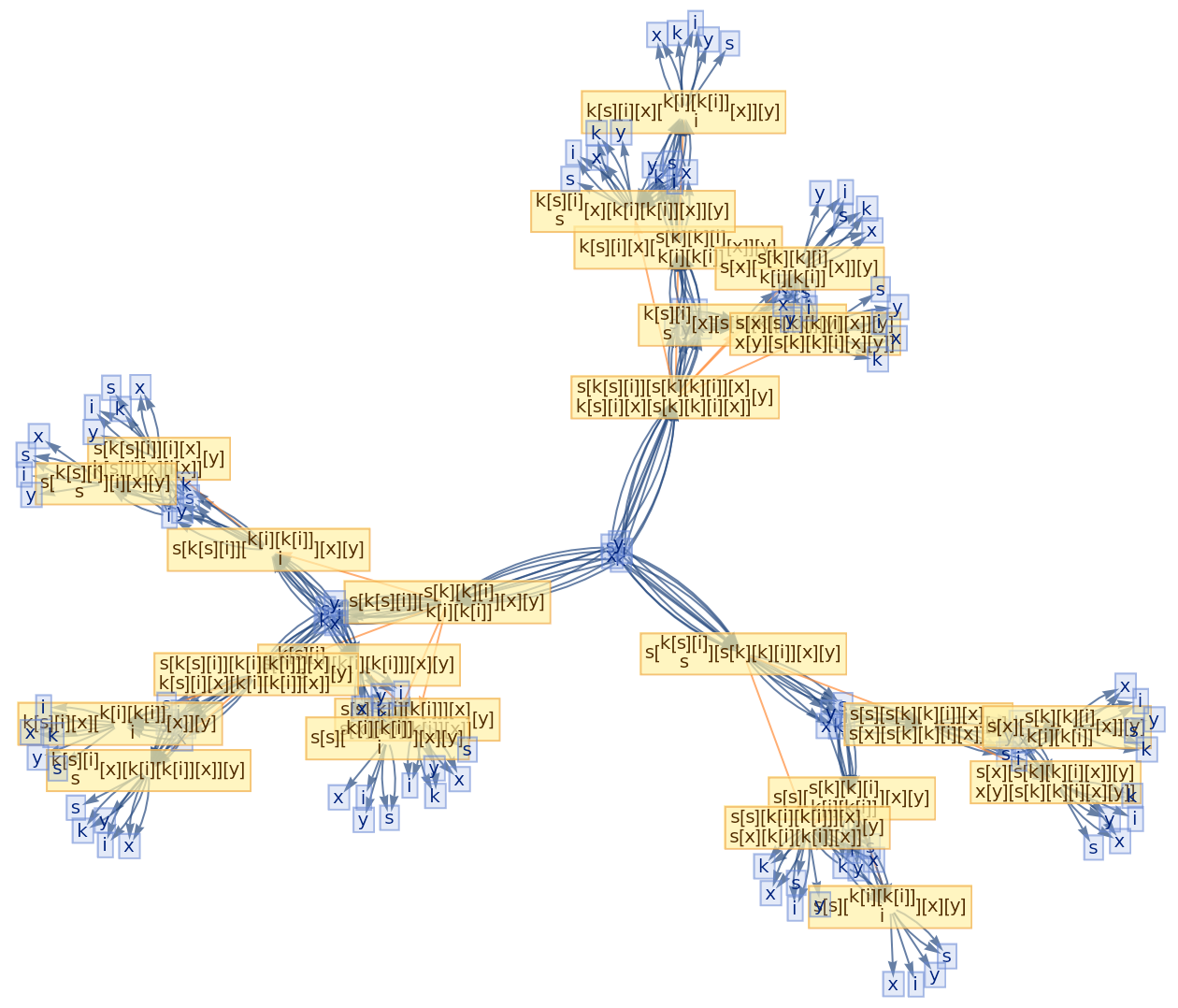
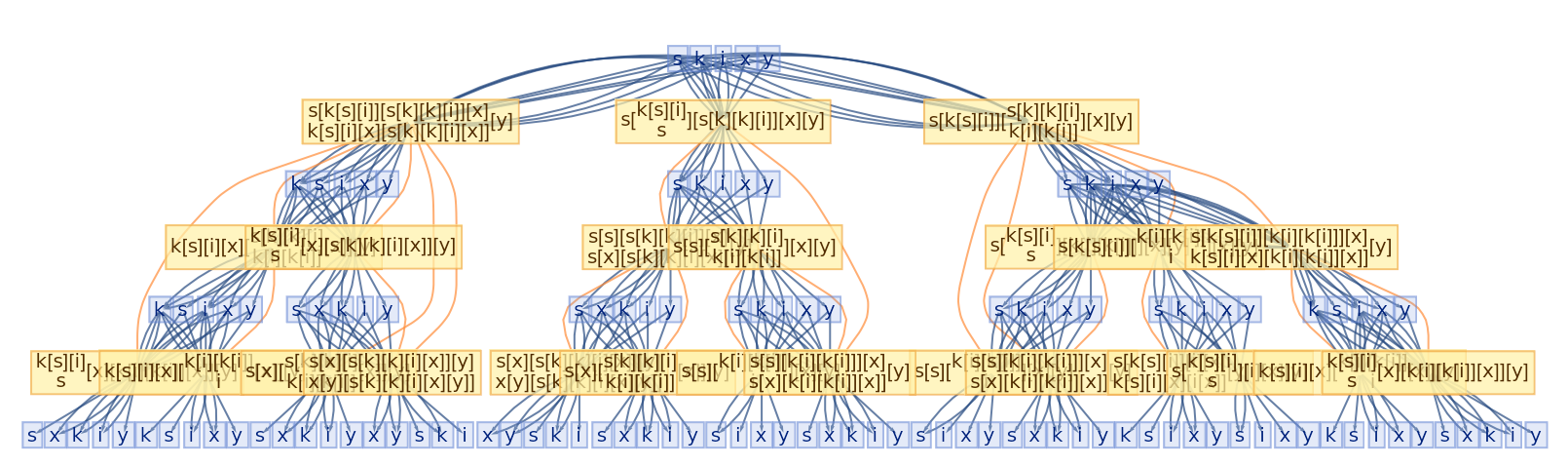
Details and Options
Glocal multiway systems combine the global events (and the corresponding causal structure) of ordinary multiway systems with the individual token philosophy of local multiway systems. A single event vertex in the evolution causal graph (or token event graph) will, in general, have many incoming and outgoing evolution edges, corresponding to the fact that several tokens must be assembled together in order to reconstruct a single global input or output state for the event.
Argument and option patterns for ResourceFunction["CombinatorGlocalMultiwaySystem"] match those of the resource function MultiwayCombinator (and, to a lesser extent, the resource function MultiwaySystem).
Rule and state specifications for ResourceFunction["CombinatorGlocalMultiwaySystem"] are rules and expressions of some combinatory calculus.
ResourceFunction["CombinatorGlocalMultiwaySystem"] accepts both individual rules of combinatory calculus and lists of rules, and likewise for initial conditions. ResourceFunction["CombinatorGlocalMultiwaySystem"][rules,init,n] is interpreted as ResourceFunction["CombinatorGlocalMultiwaySystem"][rules,{init},n] etc.
The event selection function sel in ResourceFunction["CombinatorGlocalMultiwaySystem"][rules→sel,…] can have the following special forms:
| "Sequential" | applies the first possible replacement (sequential substitution system) |
| "Random" | applies a random replacement |
| {"Random",n} | applies n randomly chosen replacements |
Duplicated tokens are displayed separately at each time step by default, although this can be overridden by setting
"DeduplicateTokens"→True.
Events are represented in the form {rule,input,rest}, where rule is the rule used in the updating event, input is the part of the state to which the rule is applied and rest is the remainder of the state. For substitution systems, rest is given in the form {prefix,suffix}.
Options for ResourceFunction["CombinatorGlocalMultiwaySystem"] include:
| "DeduplicateTokens" | False | whether to merge all instances of equivalent tokens that appear at each time step |
| "VertexRendering" | True | whether to use special rendering for state/token and event vertices |
| "IncludeInitializationEvents" | False | whether to include pseudoevents that set up initial conditions |
| "StateRenderingFunction" | Automatic | how to label states/tokens that appear in the evolution causal graph/token event graph |
| "EventRenderingFunction" | Automatic | how to label events that appear in the evolution causal graph/token event graph |
All of the standard options for the
Graph function can also be applied to
ResourceFunction["CombinatorGlocalMultiwaySystem"].
Possible settings for "StateRenderingFunction" and "EventRenderingFunction" include:
| Automatic | make a label from the name of the vertex |
| Inherited | use the explicit vertex name as the label |
| None | use no label for the vertex |
| "string" | use a shape from the VertexShapeFunction collection |
| func | apply the function func to the name of the vertex |
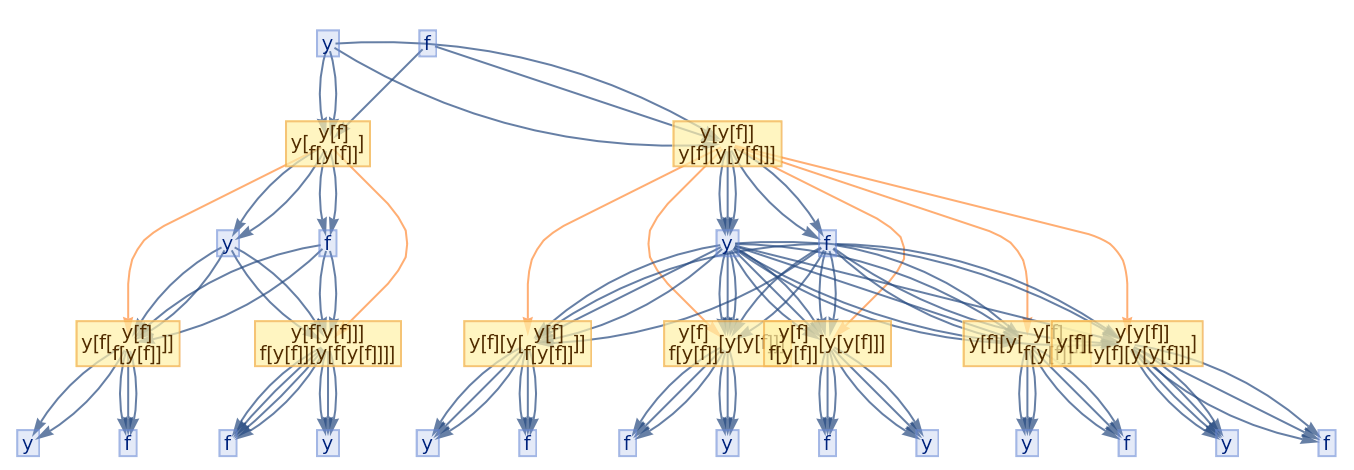
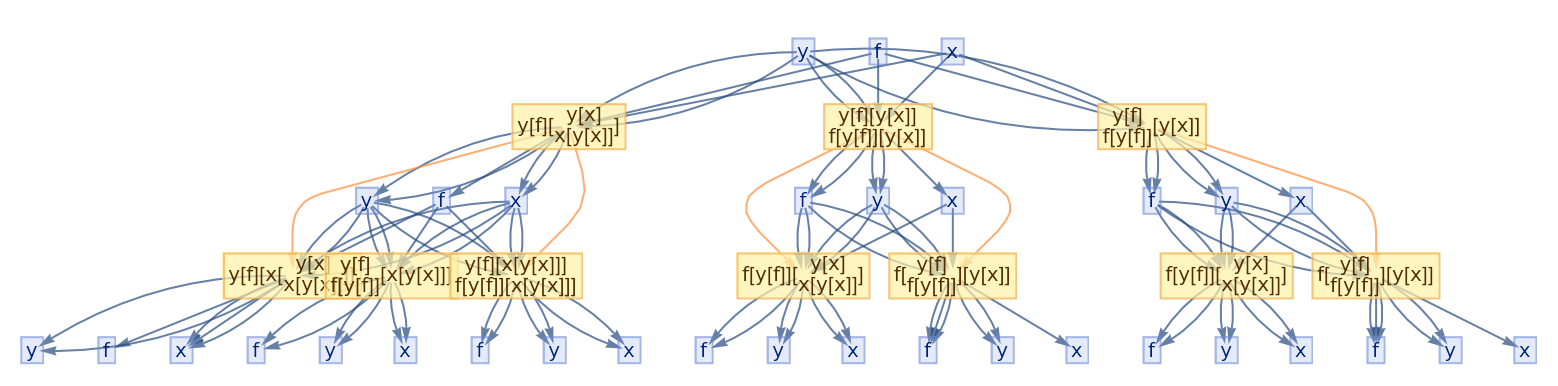
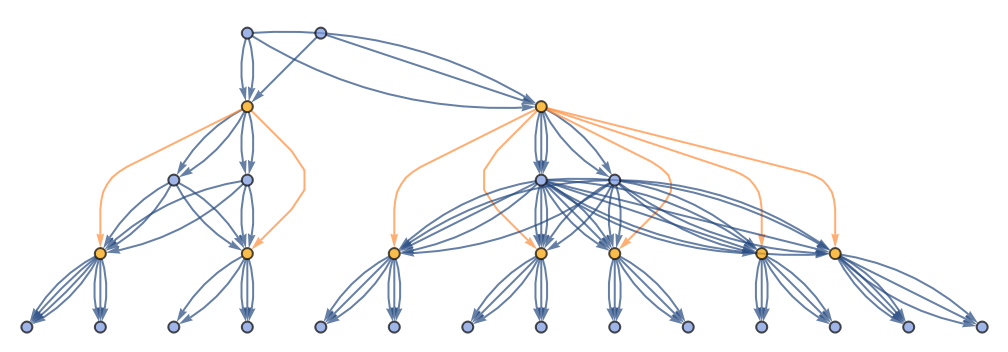

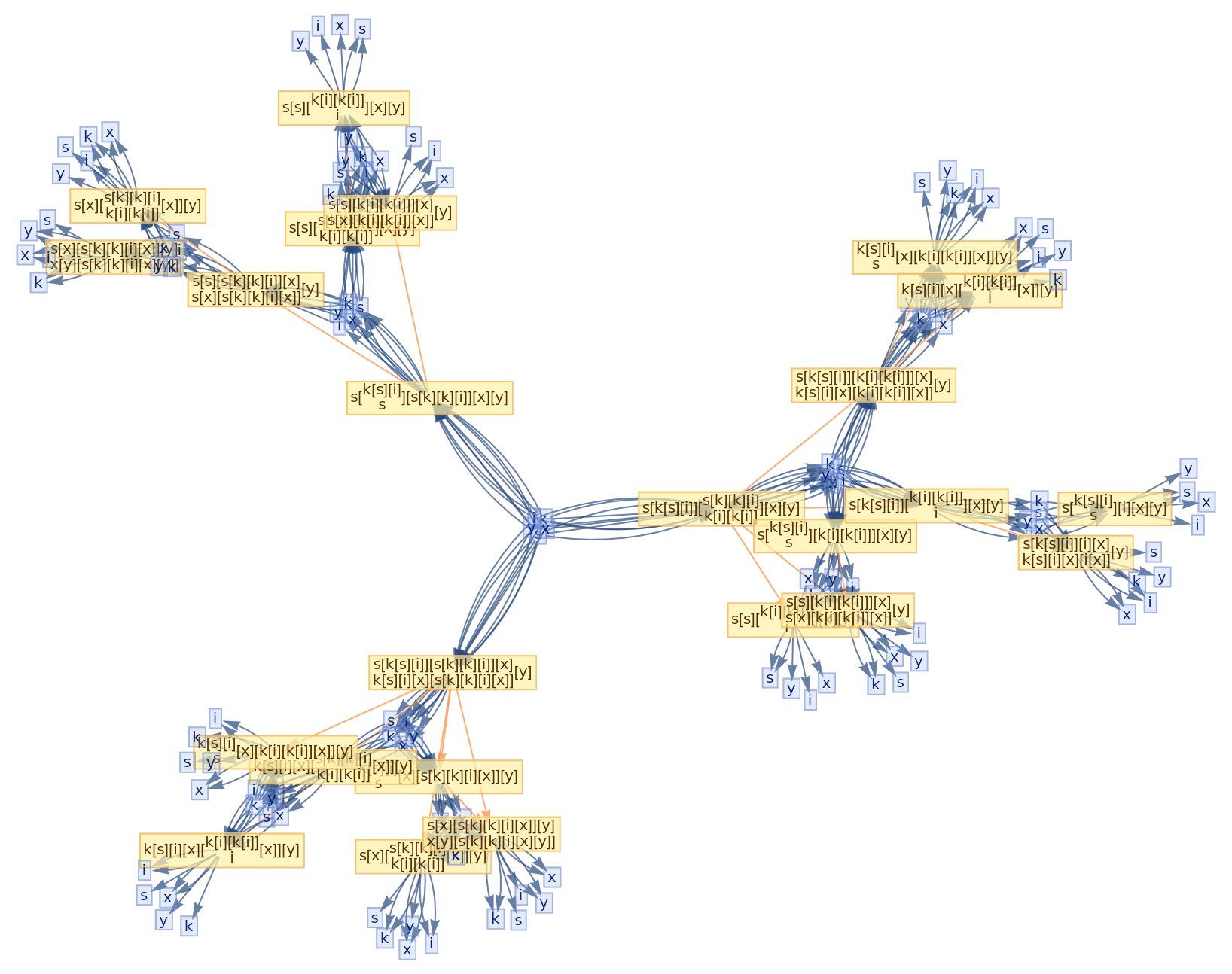
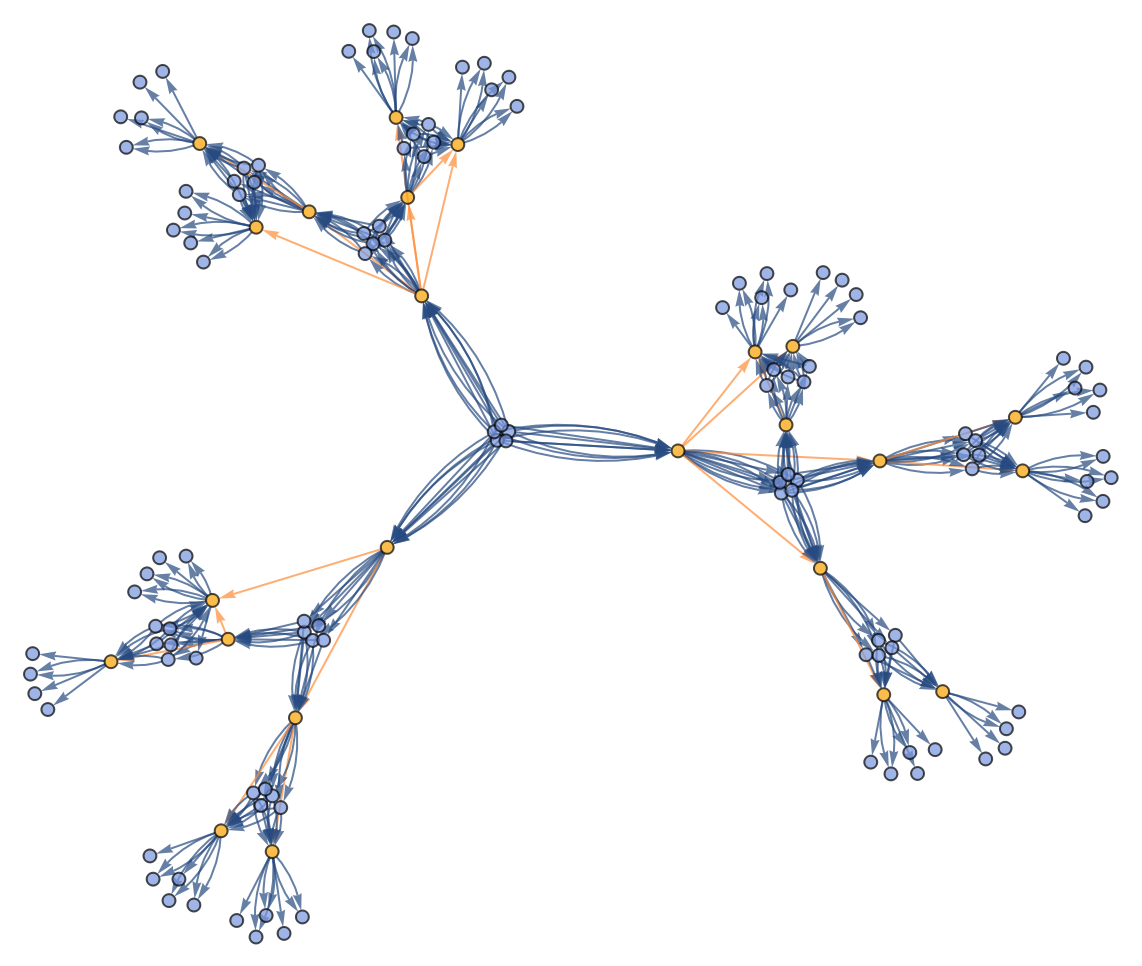
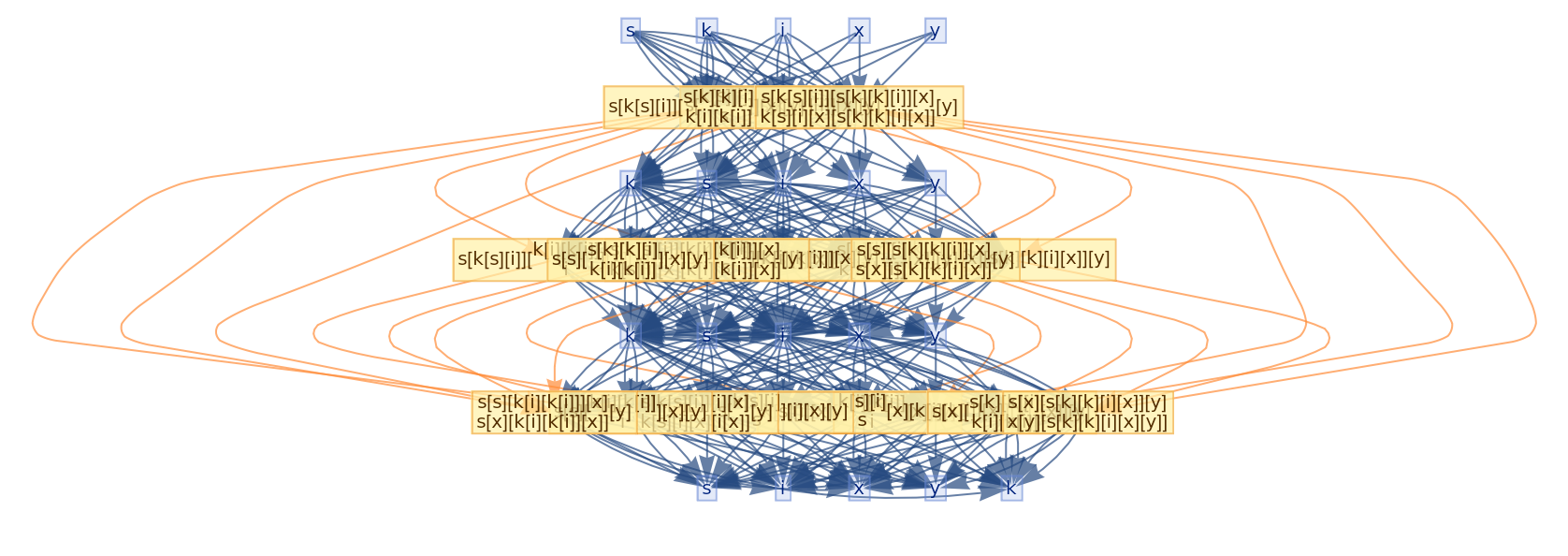
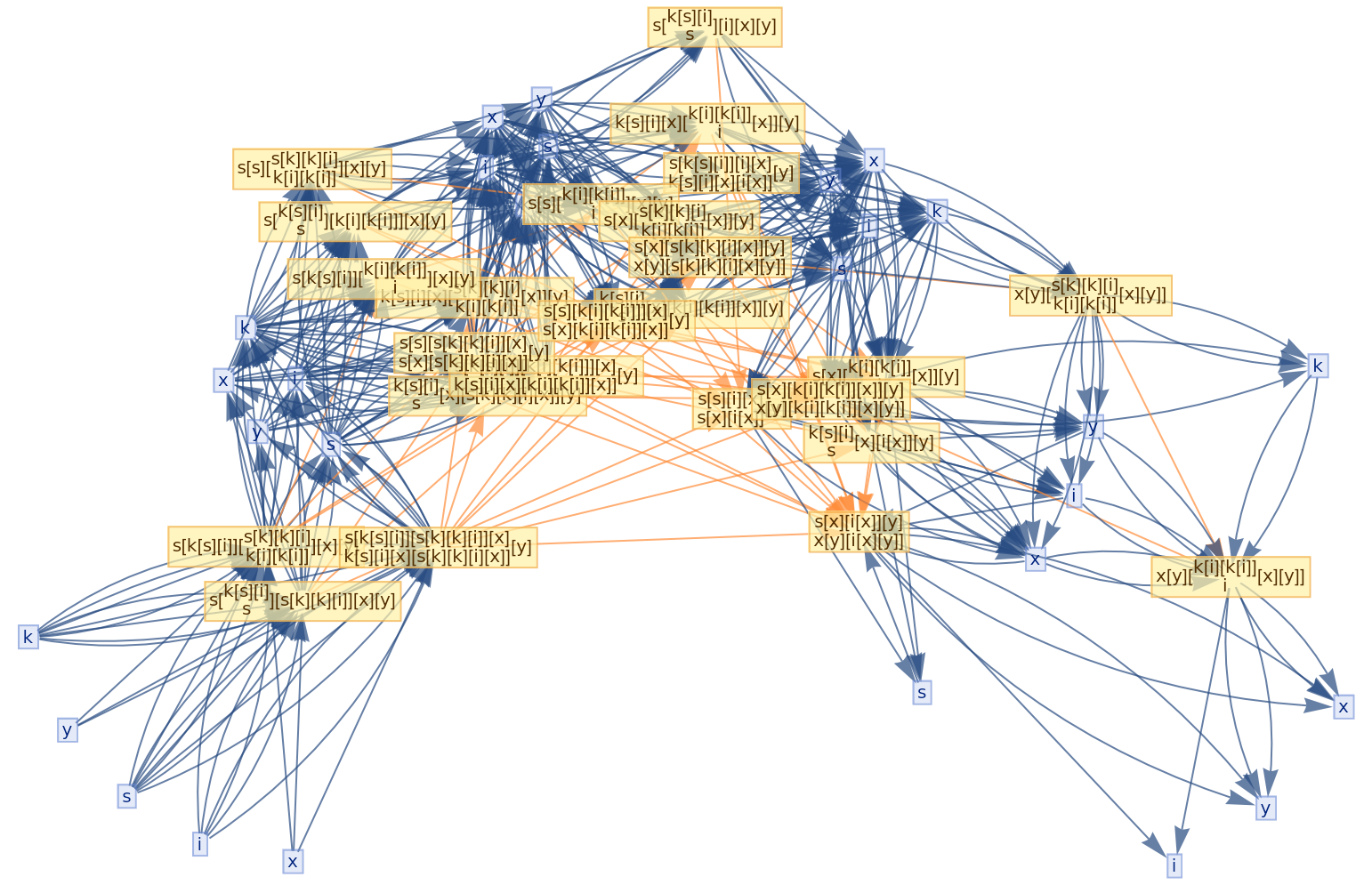

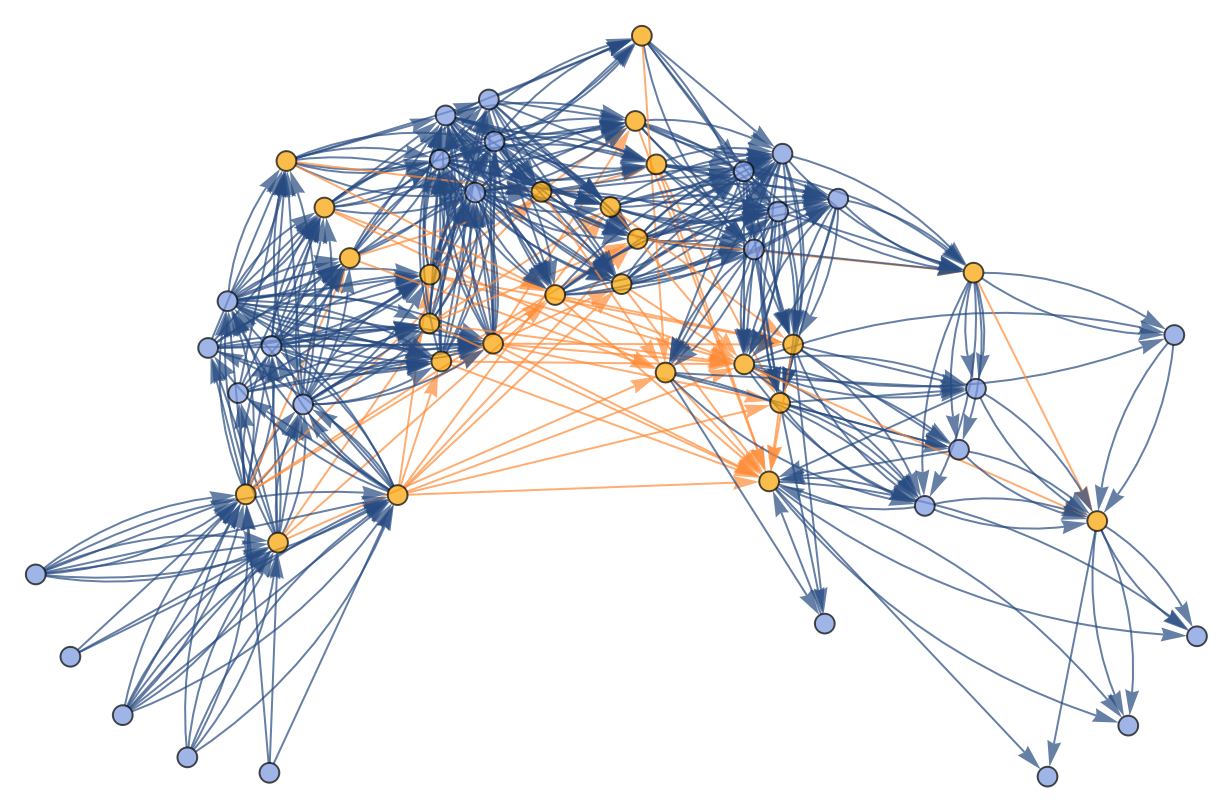
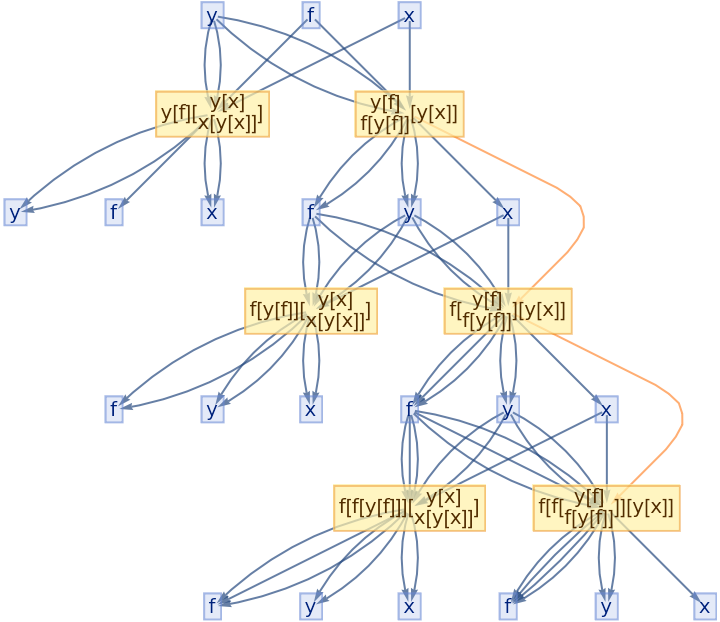
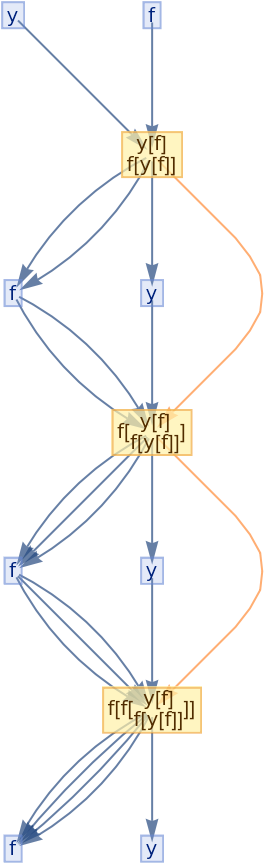
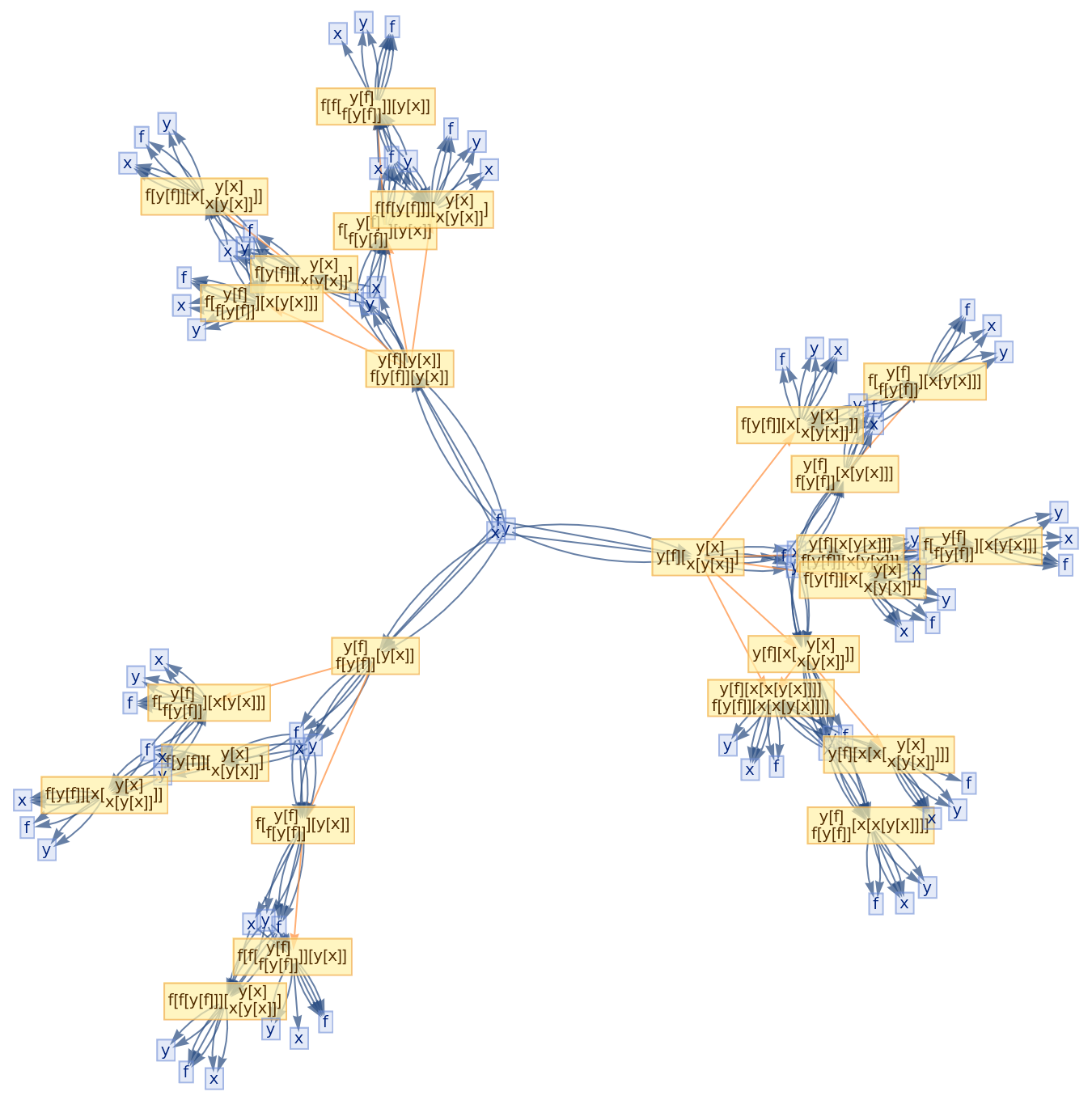
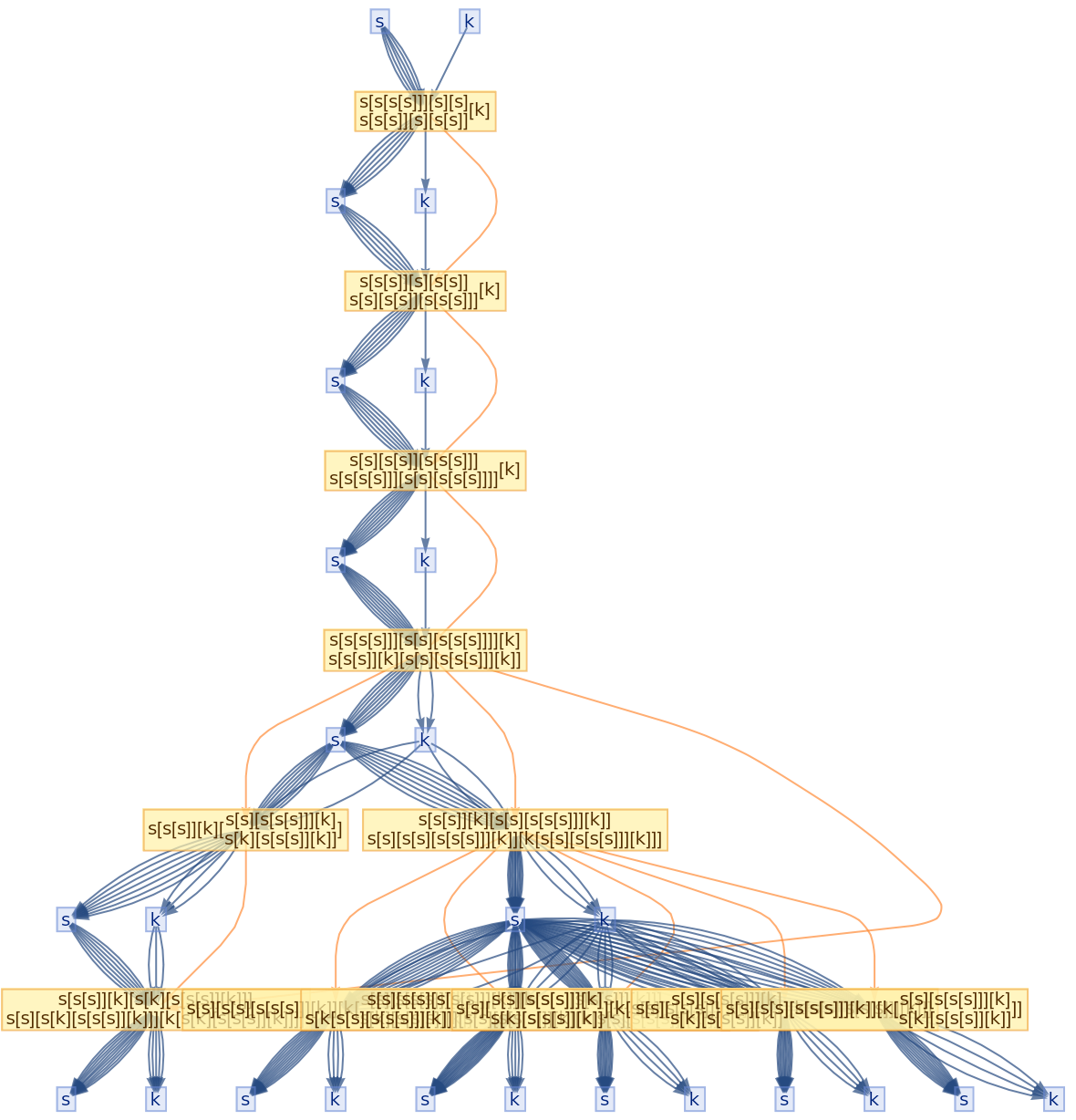
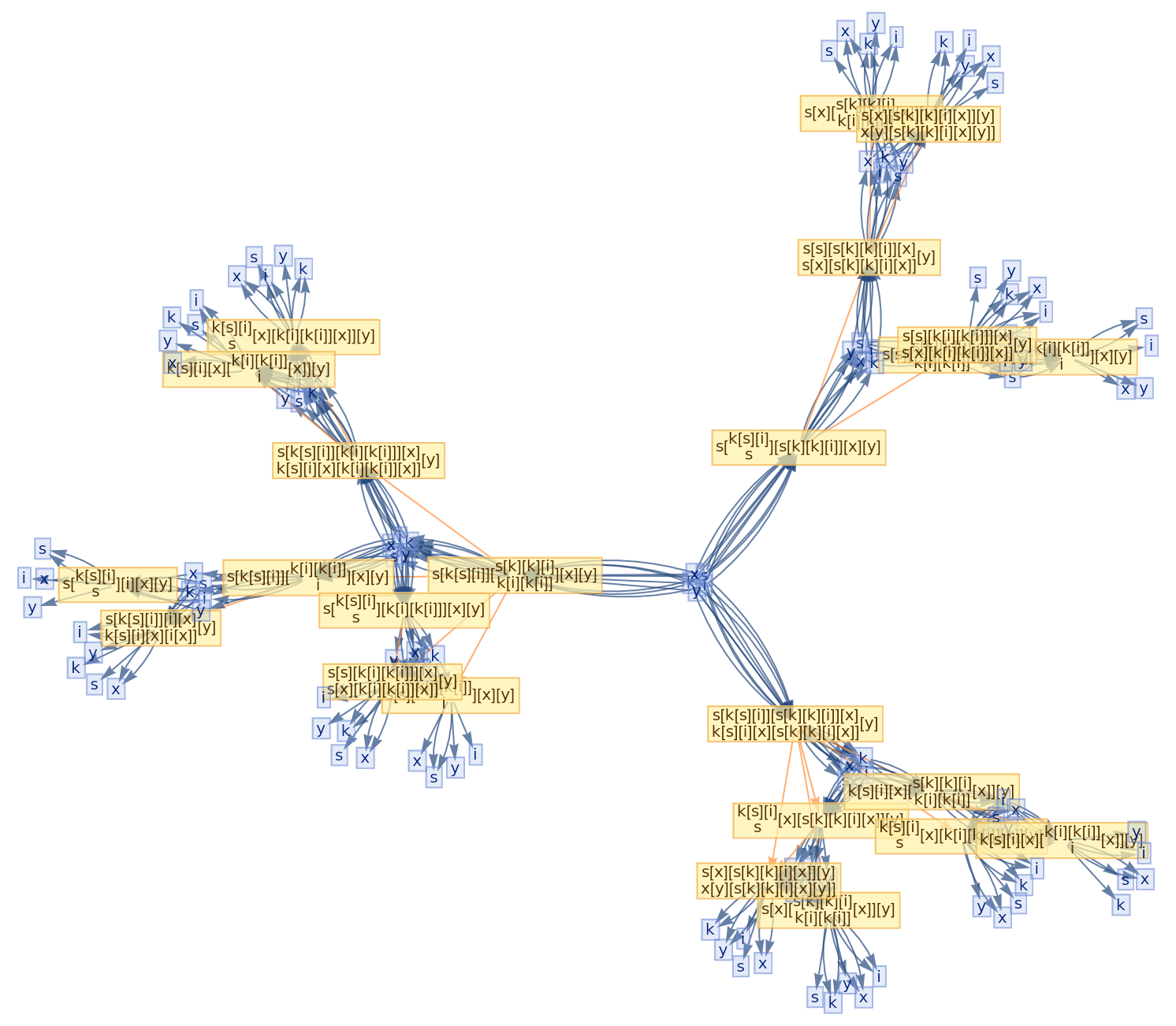
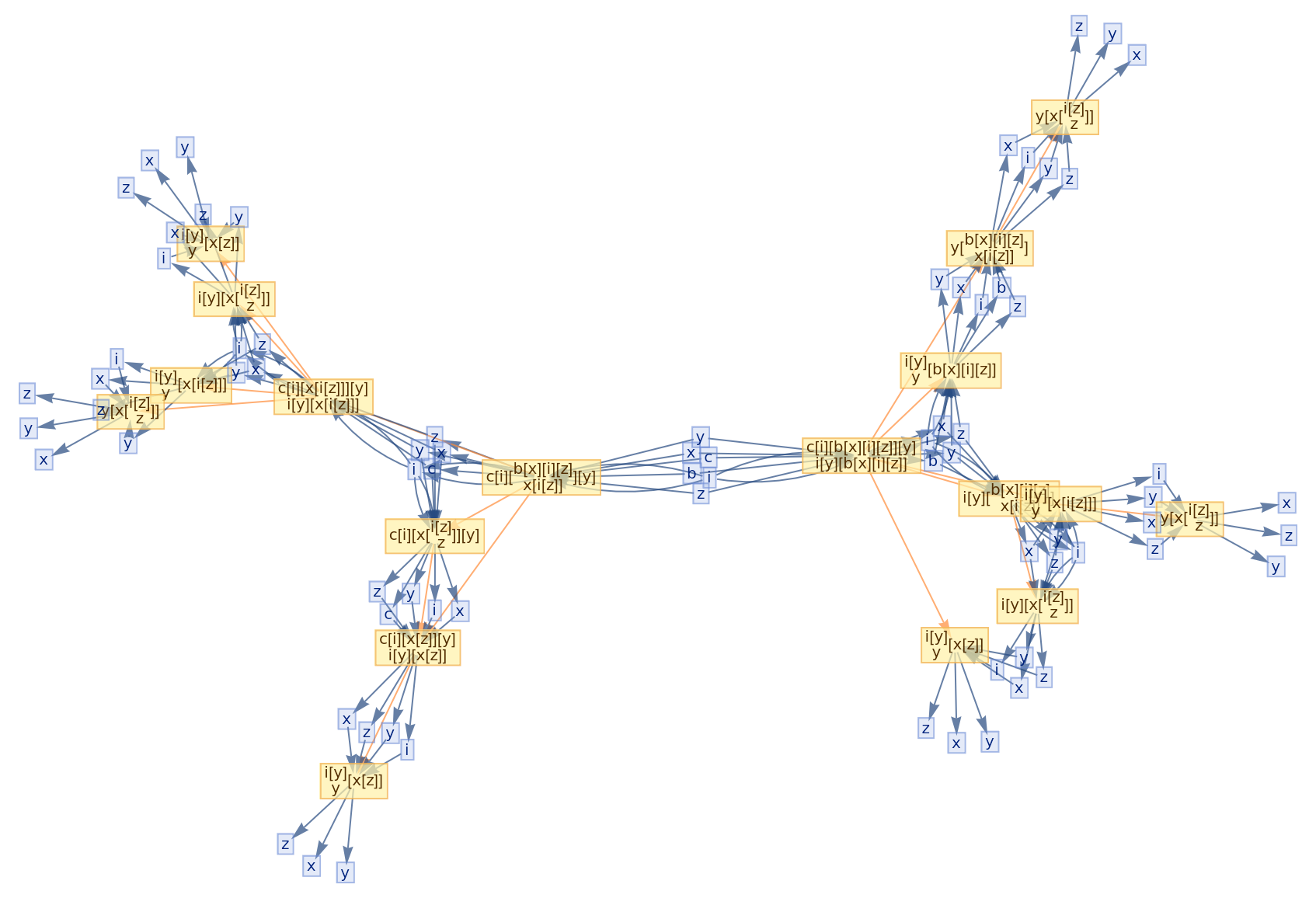
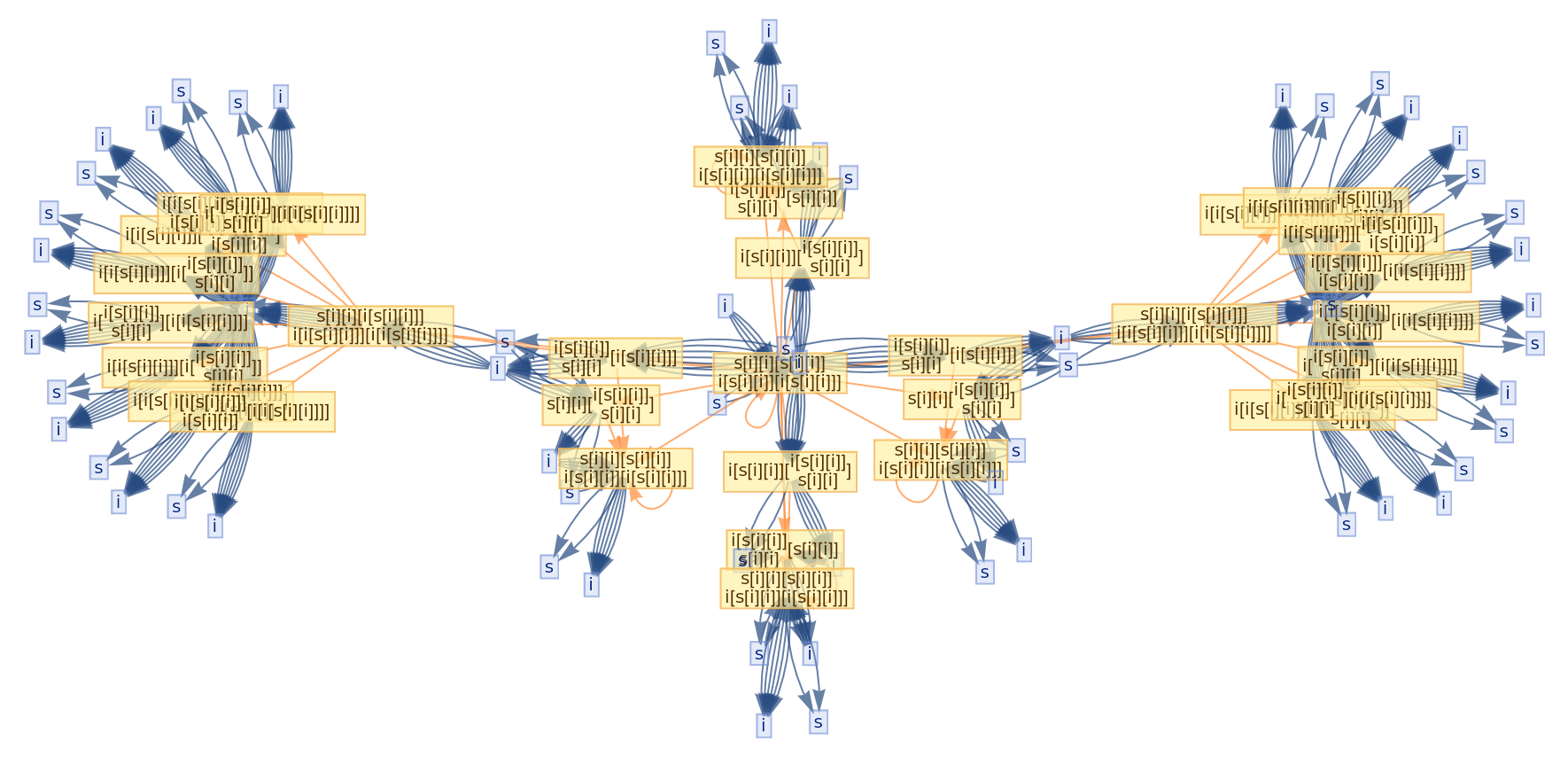
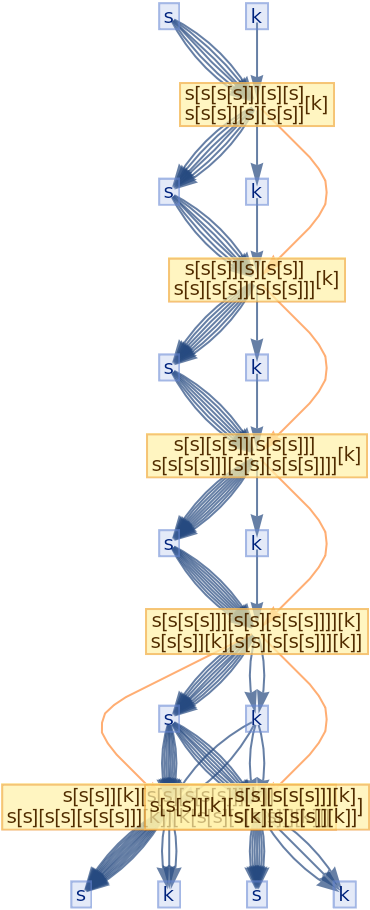
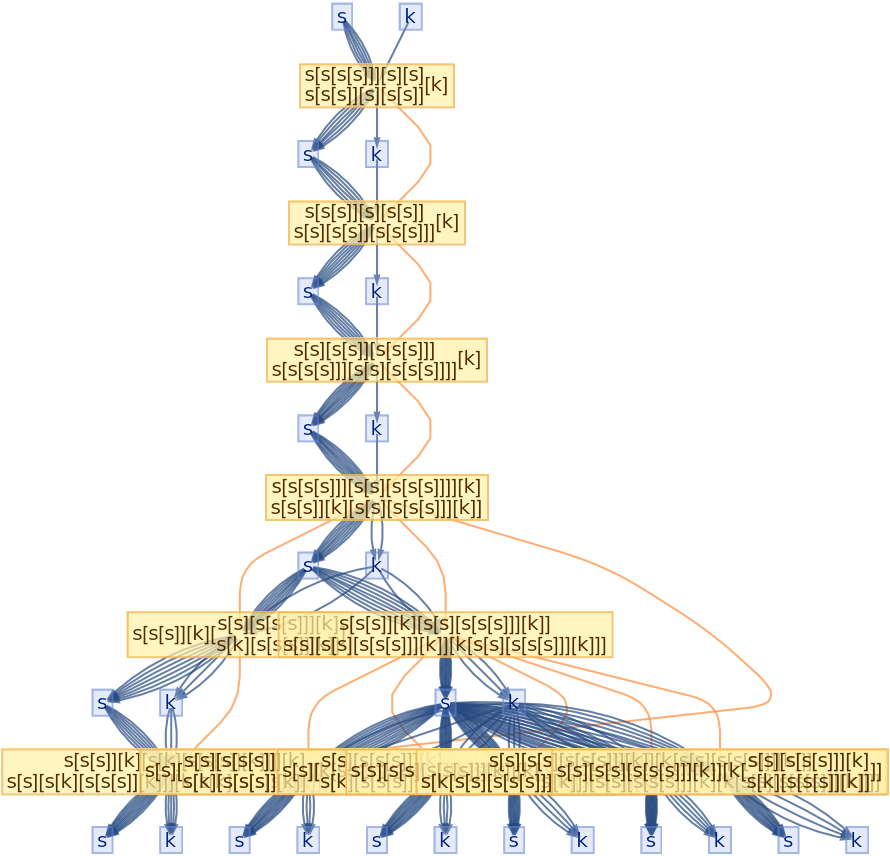
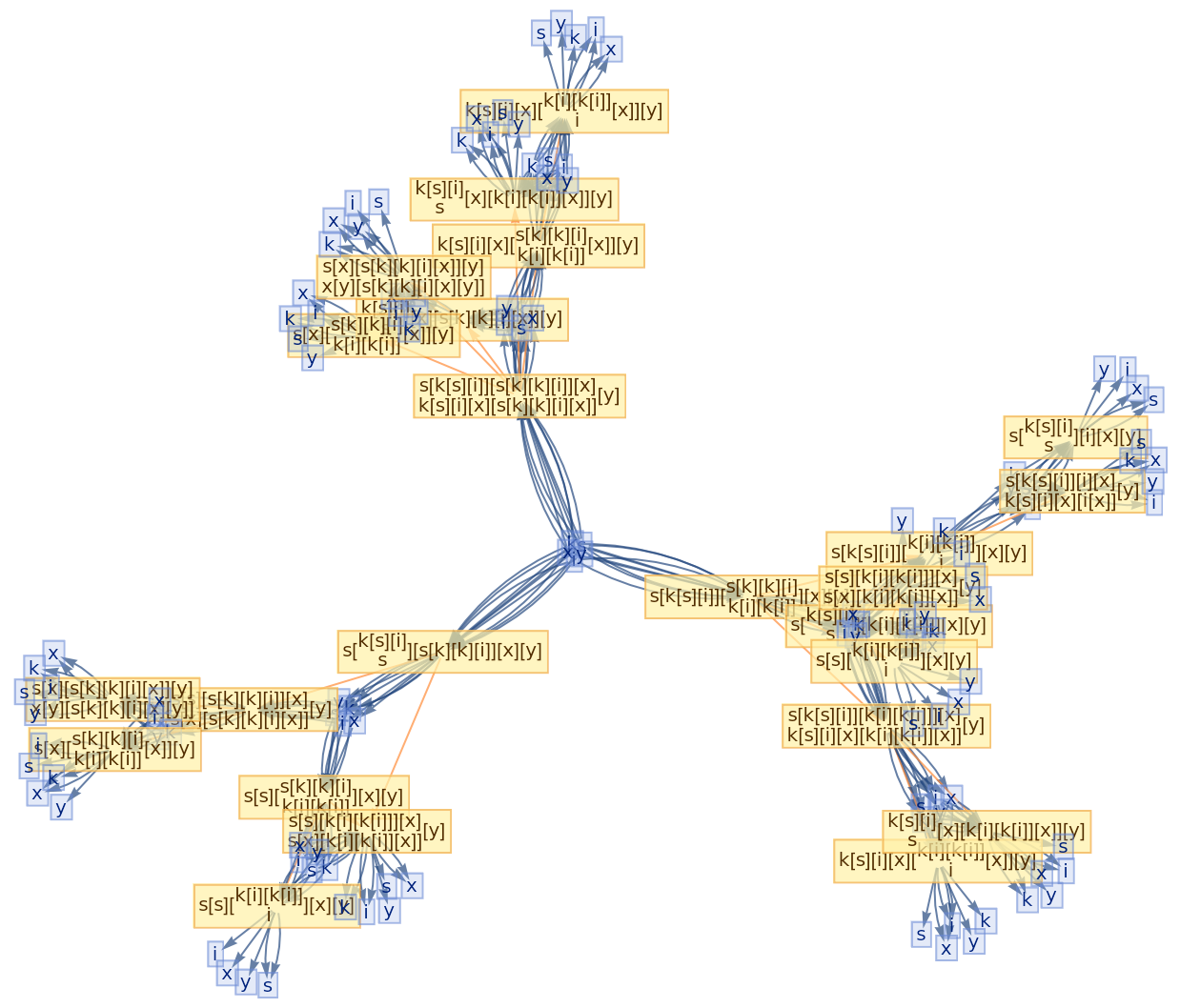
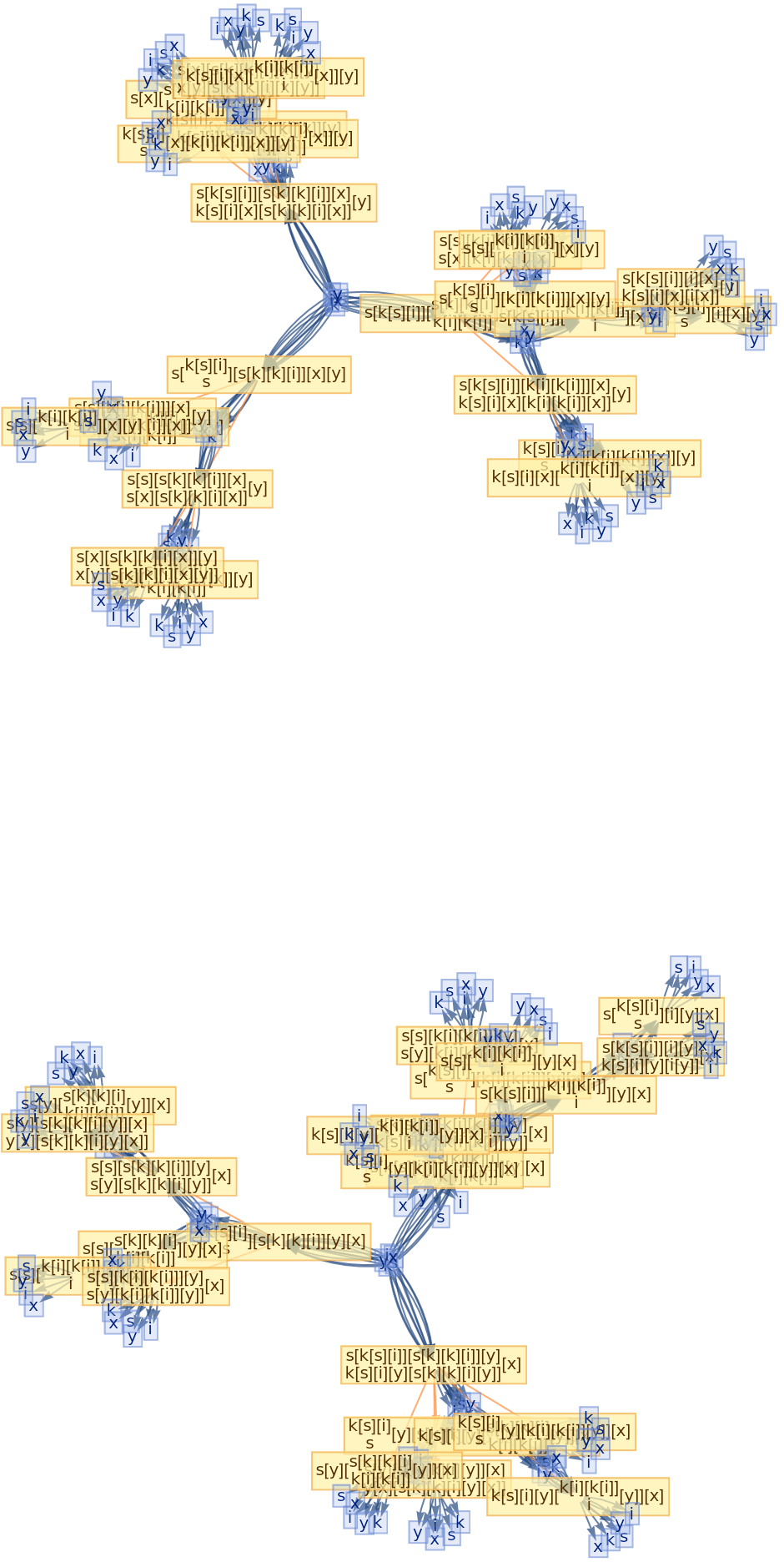
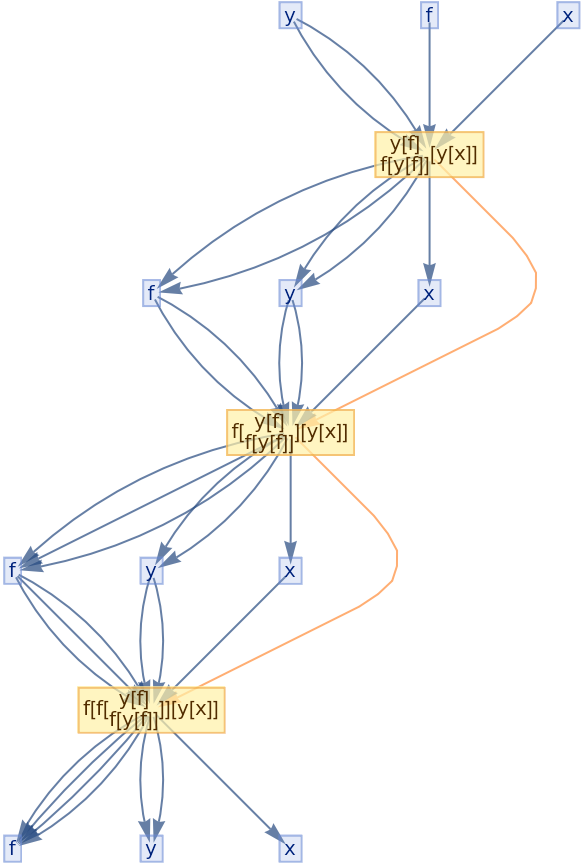
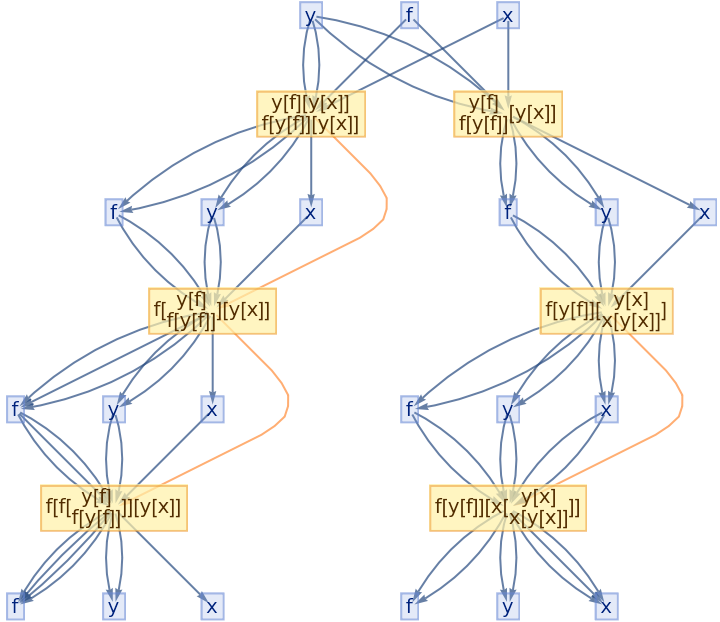
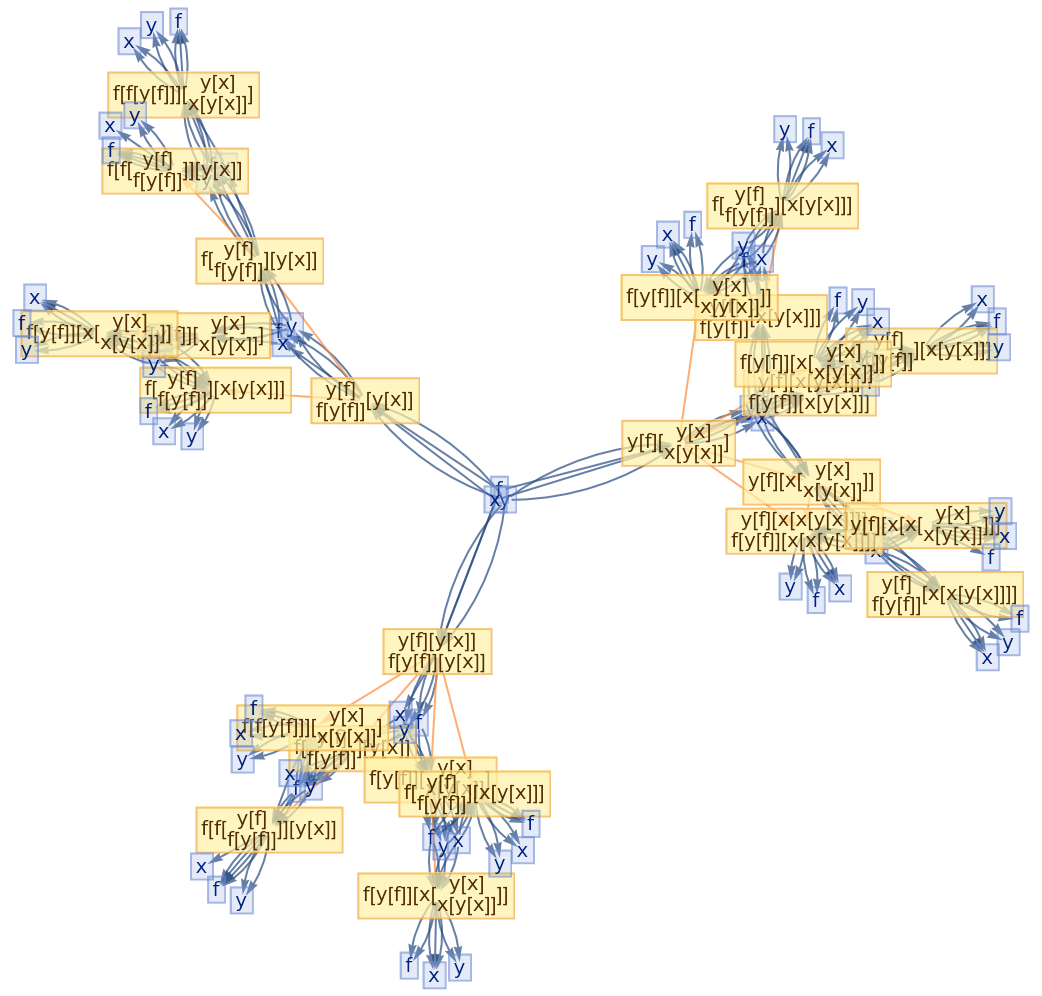
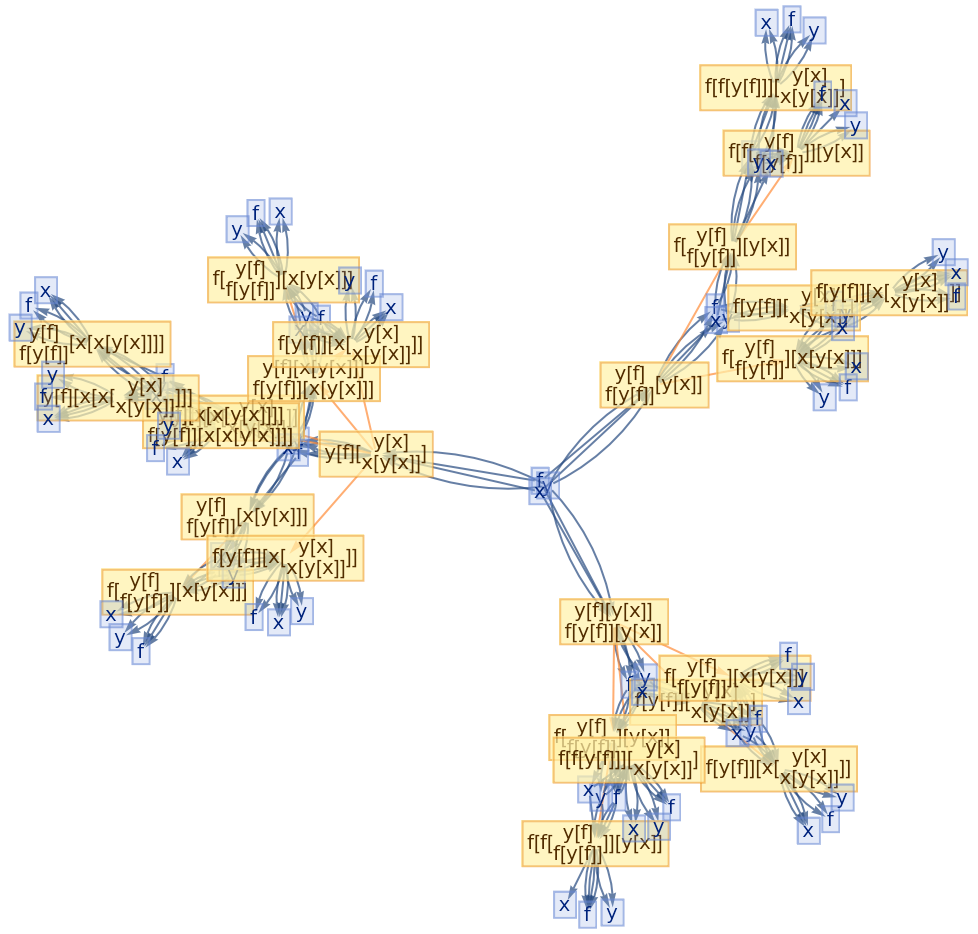
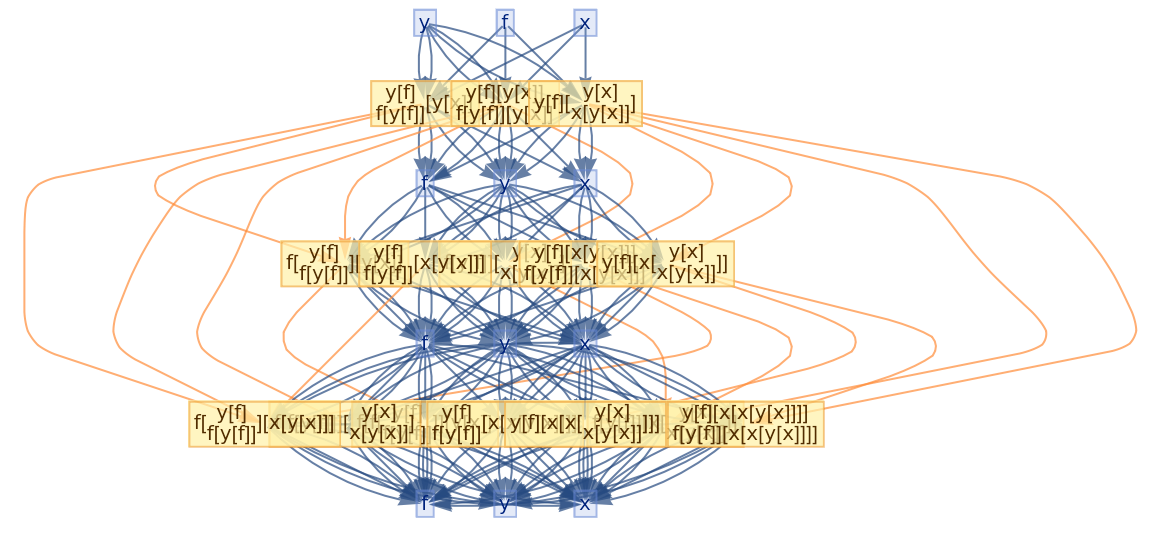
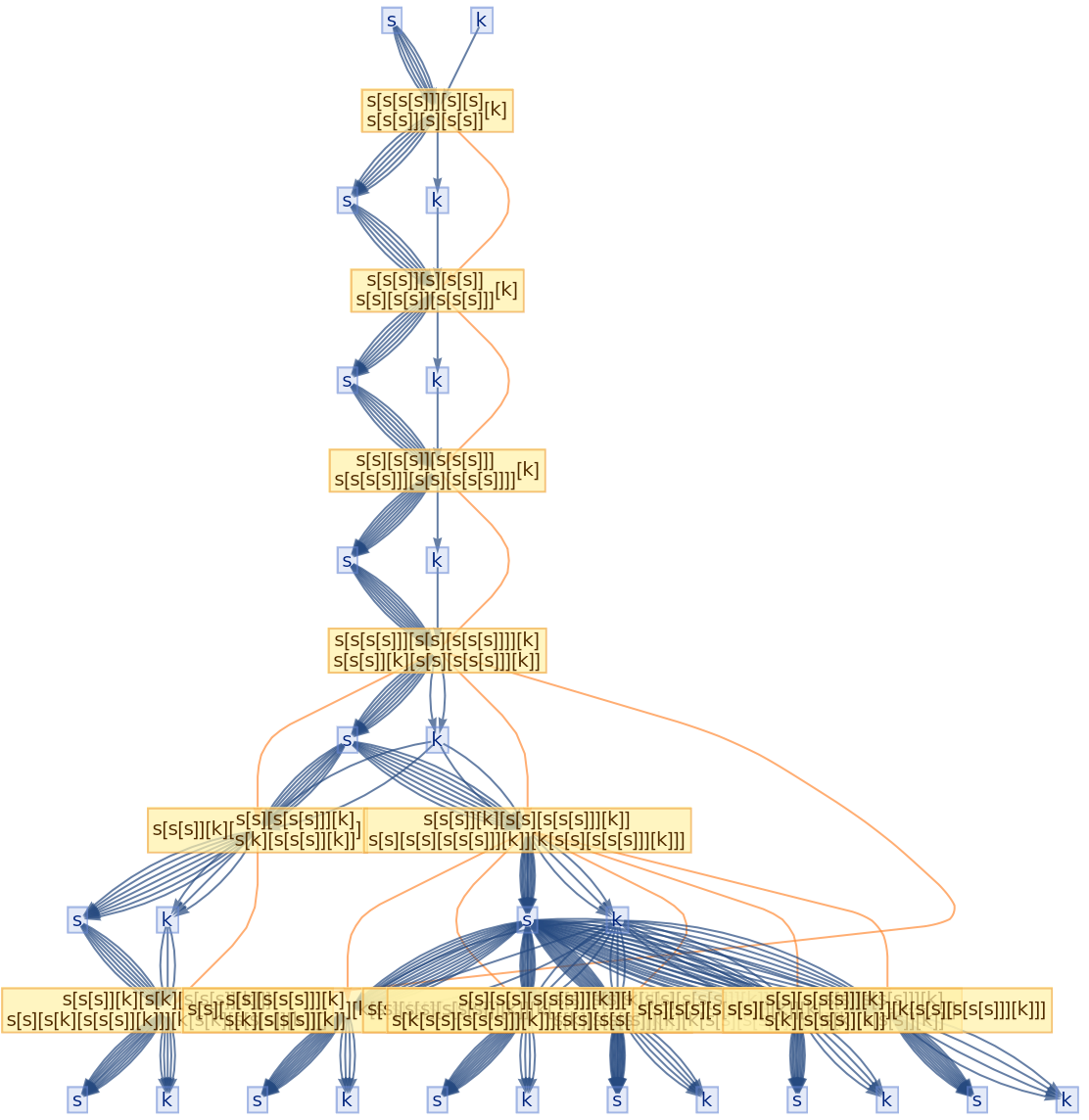
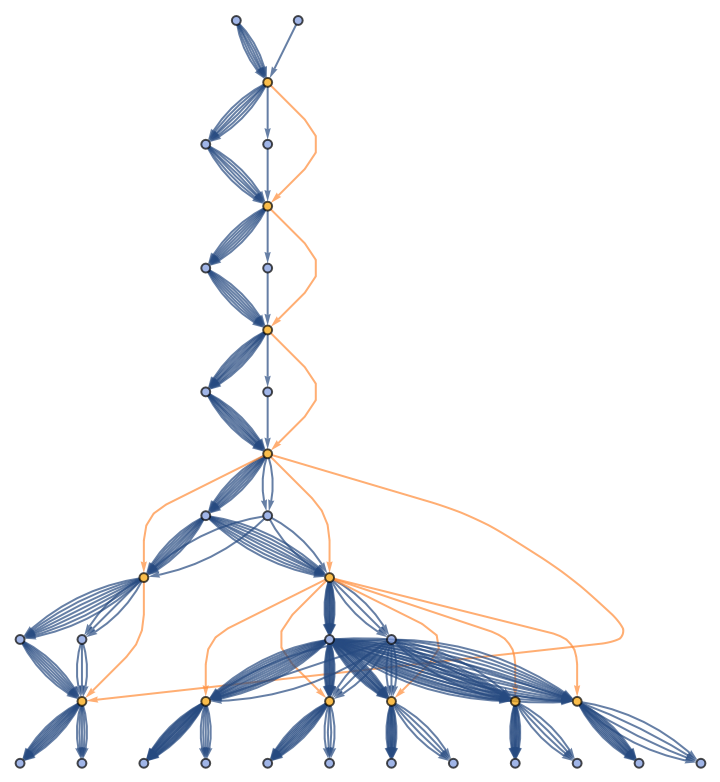
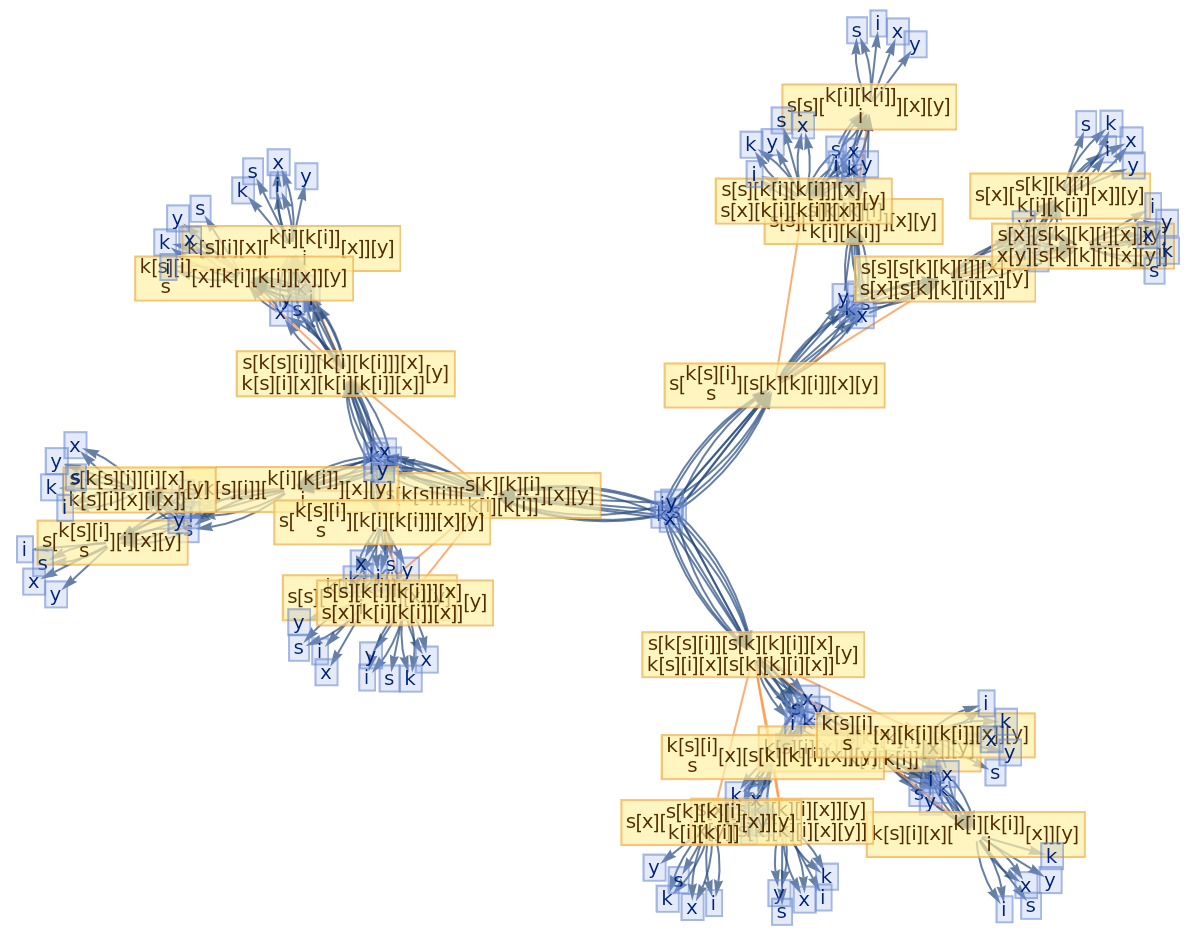
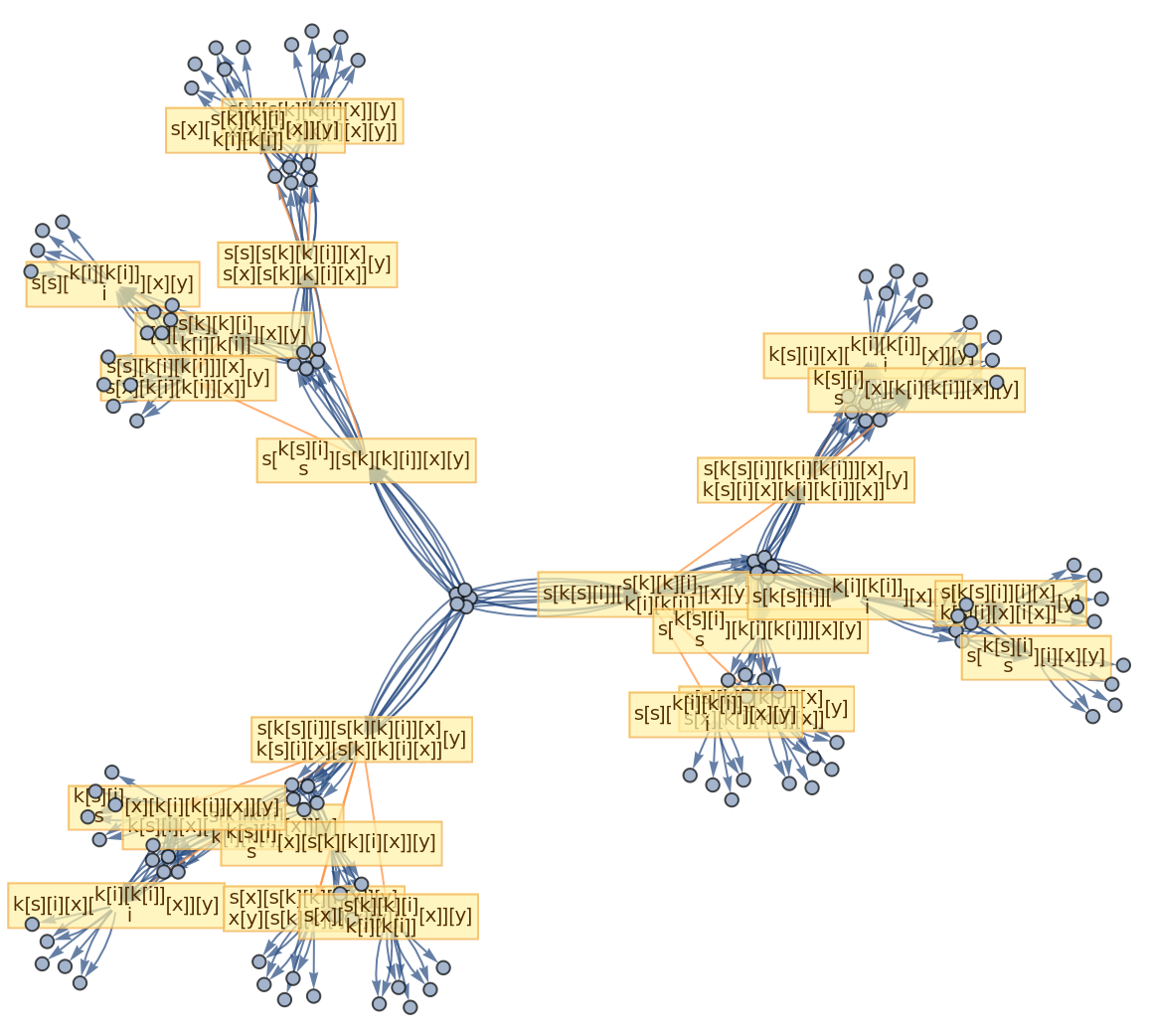
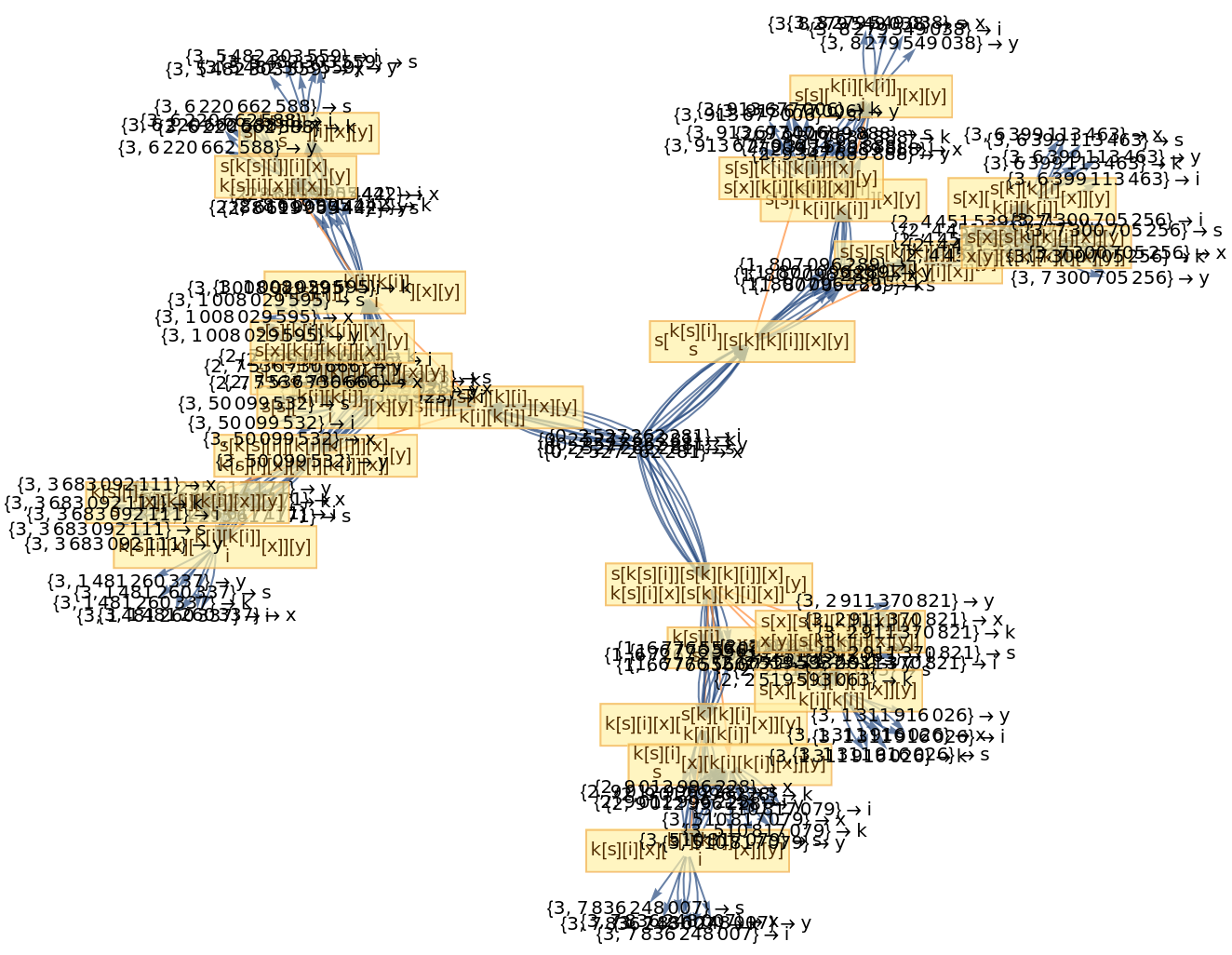
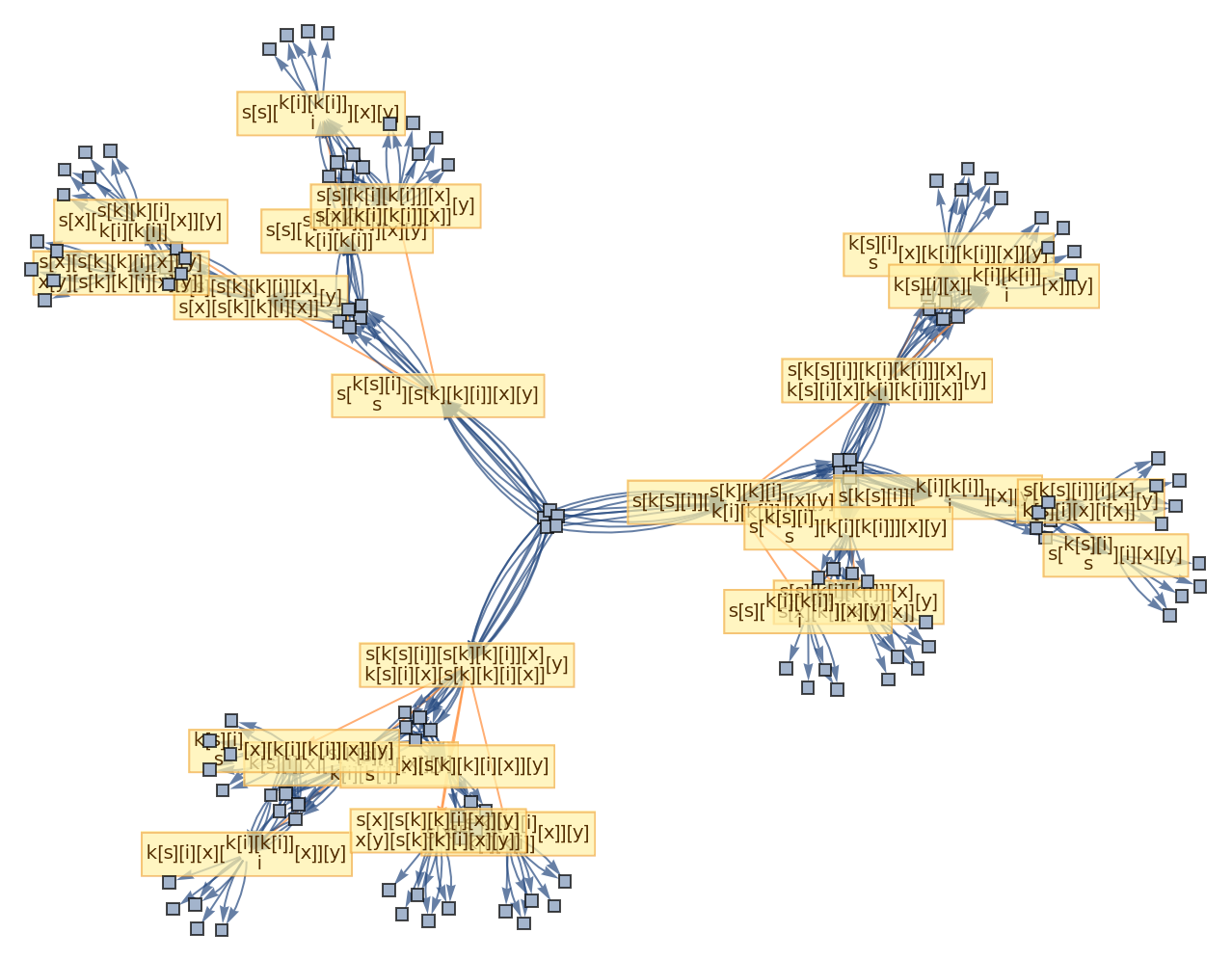
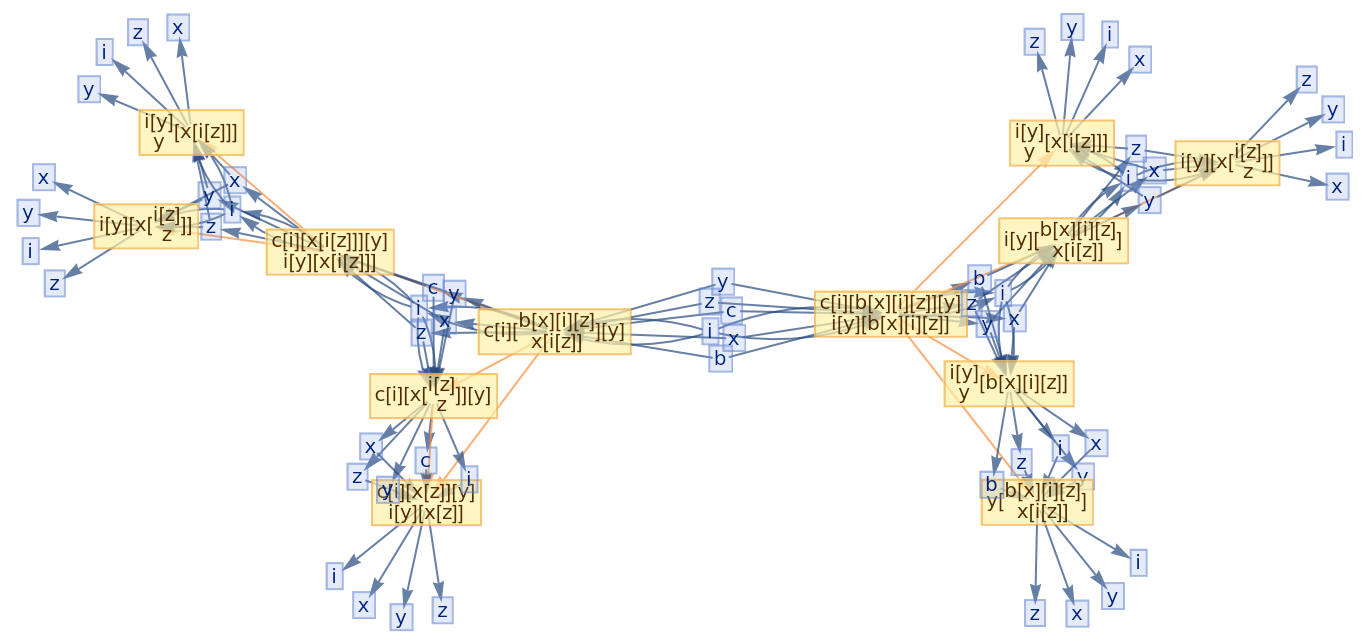
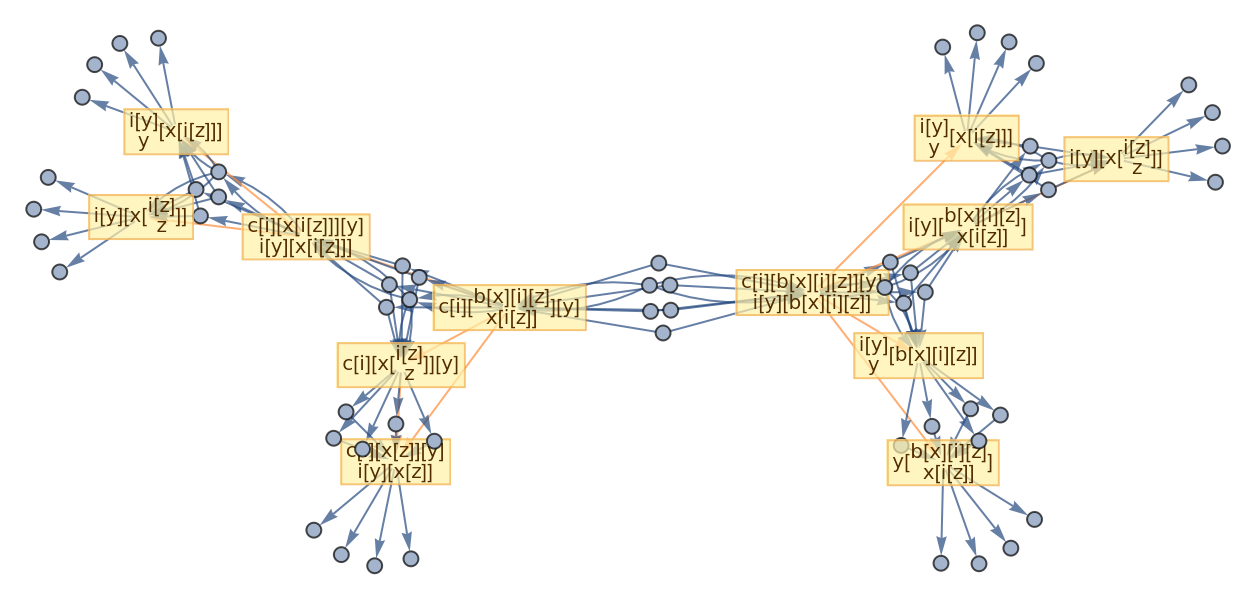
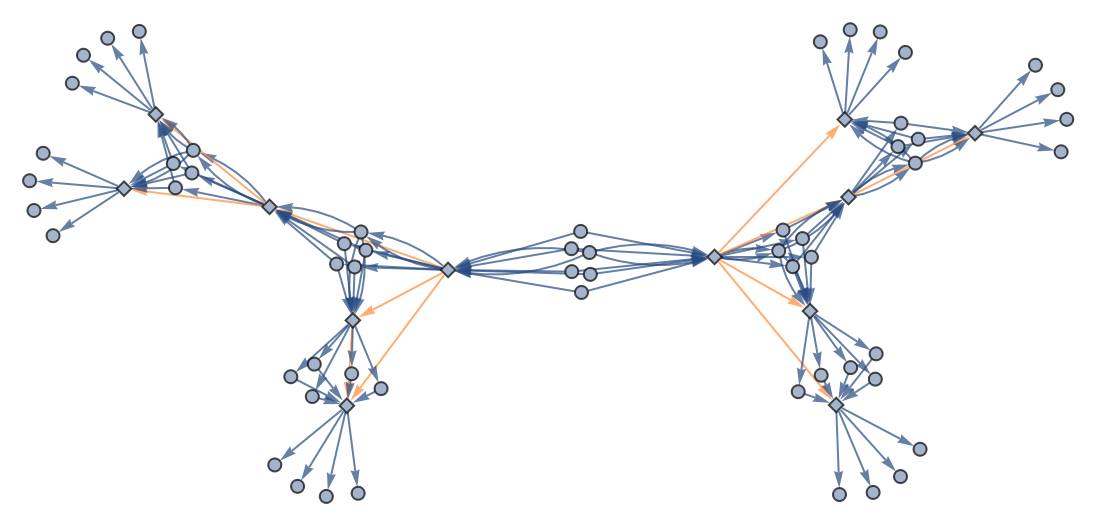
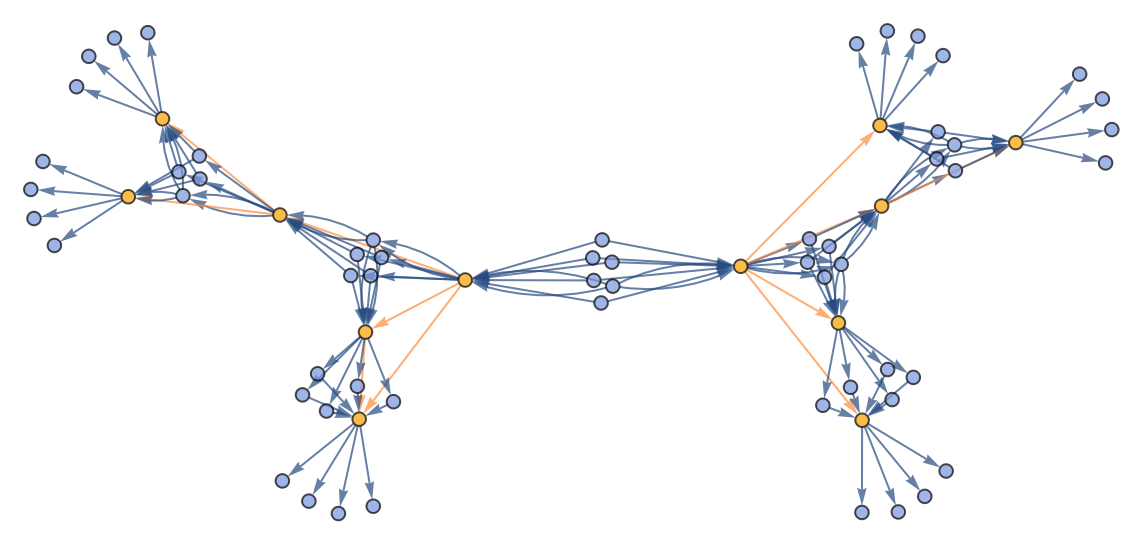
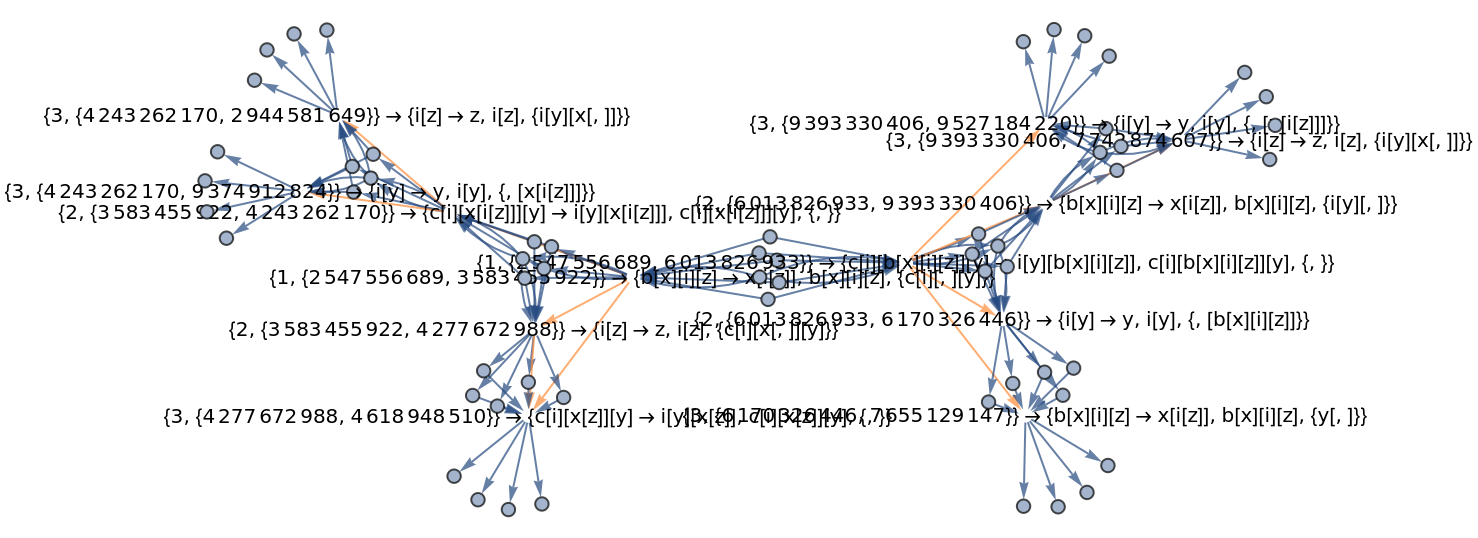
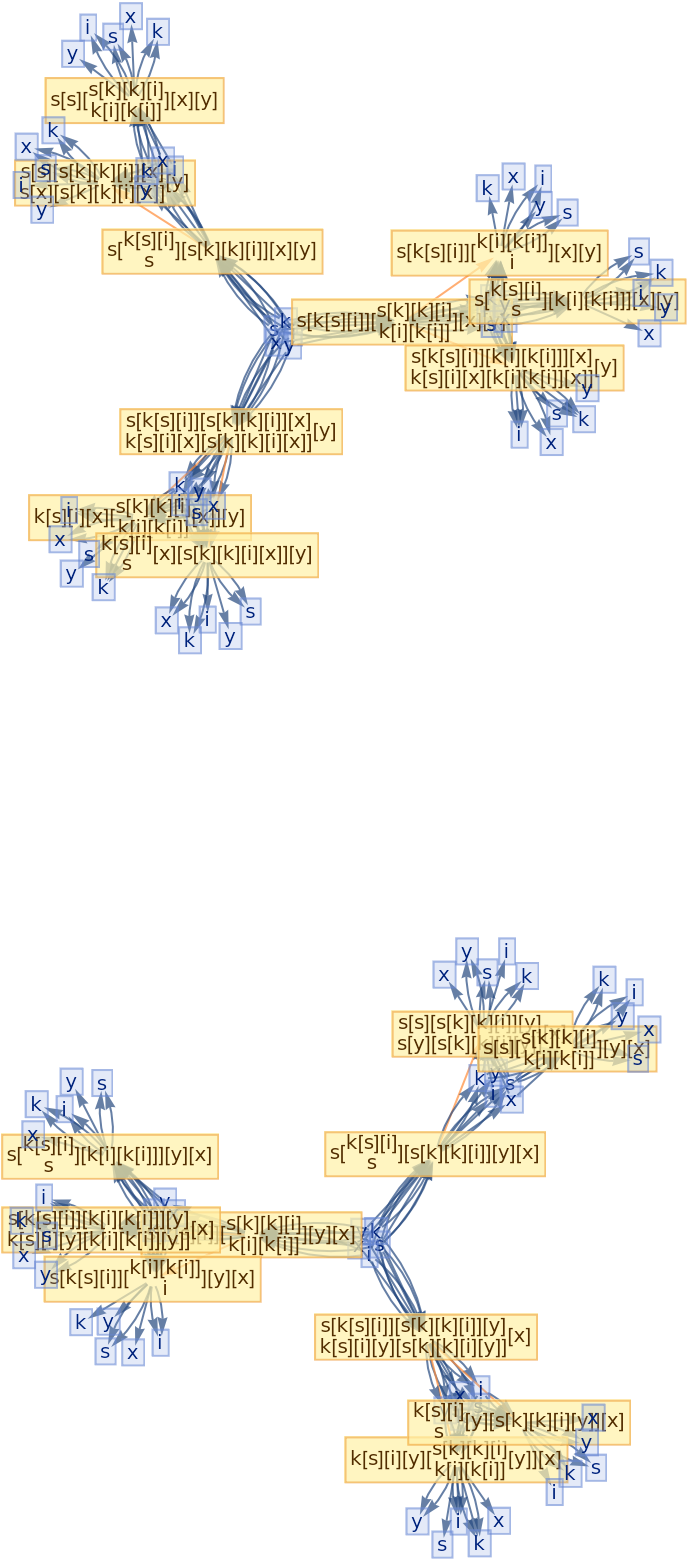
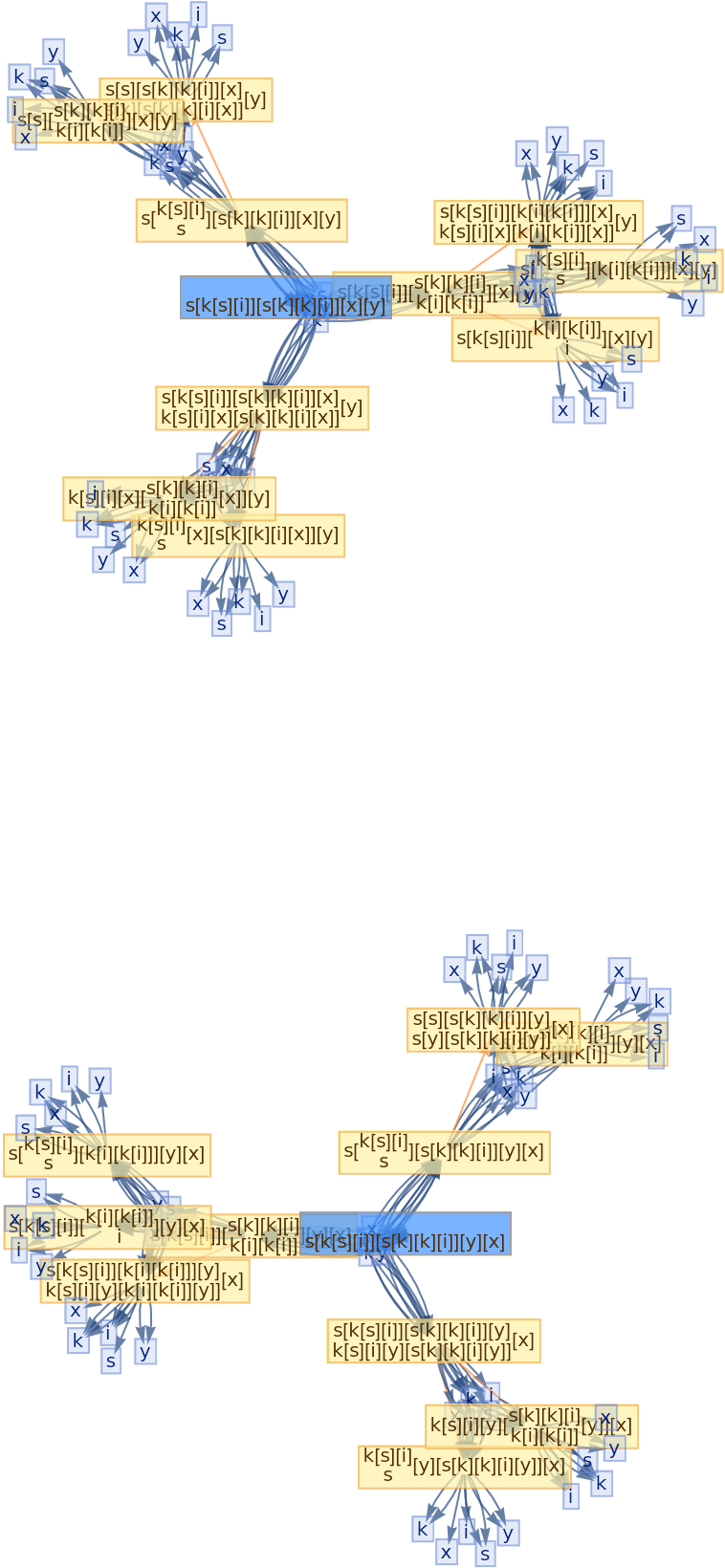
![ResourceFunction[
"CombinatorGlocalMultiwaySystem"][{s[x_][y_][z_] :> x[z][y[z]], k[x_][y_] :> x, i[x_] :> x}, {s[k[s][i]][s[k][k][i]][x][y], s[k[s][i]][s[k][k][i]][y][x]}, 2, "VertexRendering" -> False, "IncludeInitializationEvents" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/efb/efb2f2dd-6043-47c8-9e25-bf8002d245ff/6043835a31422642.png)