Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Visualize the state transformations and causal structure of a combinator evolution
ResourceFunction["CombinatorEvolutionGraph"][cmb, t, prop] displays the graph type specified by prop for a combinator expression cmb over t evolution steps. |
| "HaltedStatesGraph" | displays the multiway states graph of cmb over t evolution steps, sizing nodes according to leaf count and highlighting nodes representing halted states |
| "PathHighlight" | displays "HaltedStatesGraph" of cmb over t evolution steps, but also highlights one path in the graph according to the specified option value for "EvaluationScheme" |
| "CausalGraph" | displays the causal structure of cmb over t evolution steps; takes the causal graph instance corresponding to the specified option value for "EvaluationScheme" |
| "MinimalHaltedStatesGraph" | False | whether to include the leaf count as a vertex label in "HaltedStatesGraph" |
| "NodeSizeMultiplier" | 0.75 | scalar factor for the node size in "HaltedStatesGraph" |
| "PathThickness" | 2.5 | edge thickness for the highlighted path in "PathHighlight" |
| "CombinatorRules" | Automatic | combinator rules used to evolve cmb |
| "SKGlyphs" | Automatic | glyphs used for S and K combinators in cmb |
| "EvaluationScheme" | {"Leftmost", "Outermost", 1} | evaluation scheme used to evolve cmb |
| "RenderCausalEvents" | False | whether to display causal events as vertices of "CausalGraph" |
Show the states graph of a combinator evolution, with labeled vertices sized according to the leaf count of the state; terminal states indicated by a thick, dark border; and states that can be further evolved indicated by a thick, orange border:
| In[1]:= |
| Out[1]= | 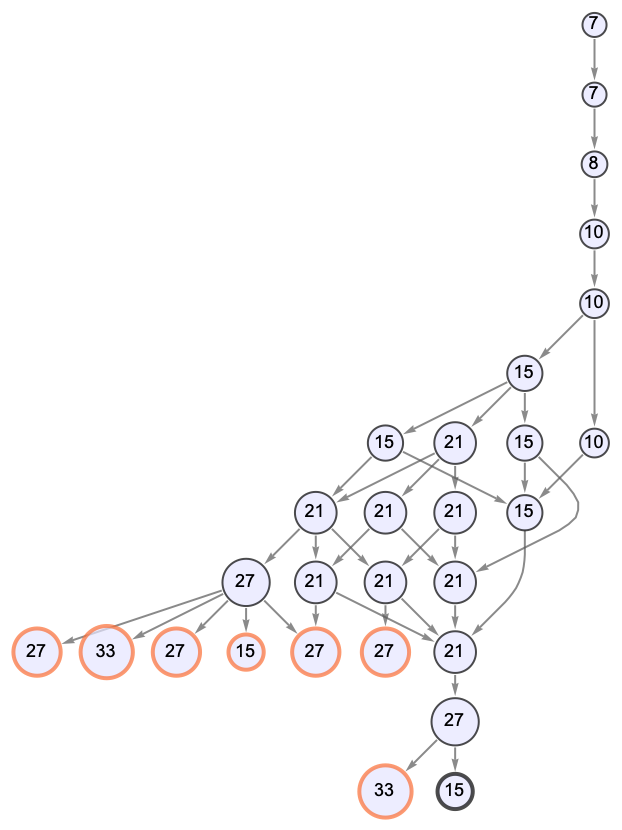 |
Highlight a path in the halted states graph of a combinator evolution according to the leftmost-outermost evaluation scheme; notice that other states attainable at the given time step are colored in a darker blue than the rest of the vertices:
| In[2]:= |
| Out[2]= | 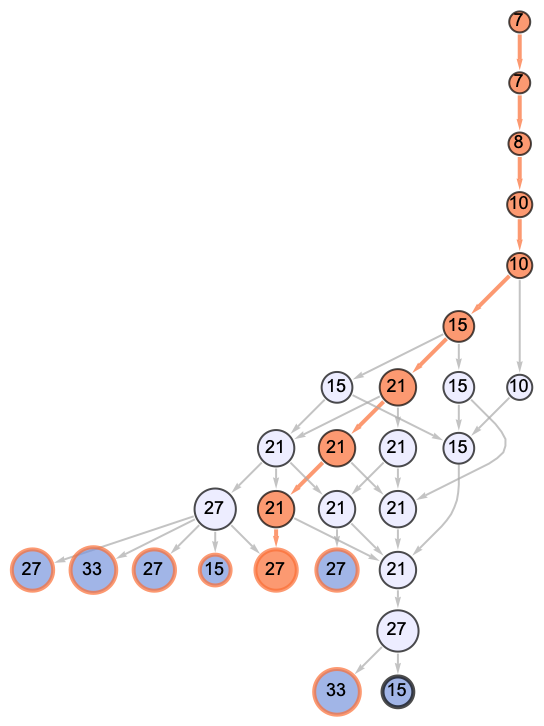 |
Show the causal structure of events in a combinator evolution according to the leftmost-outermost evaluation scheme:
| In[3]:= |
| Out[3]= | 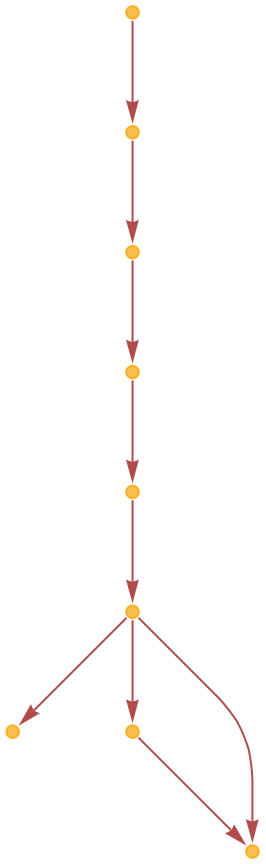 |
Specify the rules used to evolve a combinator expression and show a halted states graph:
| In[4]:= |
| Out[4]= | 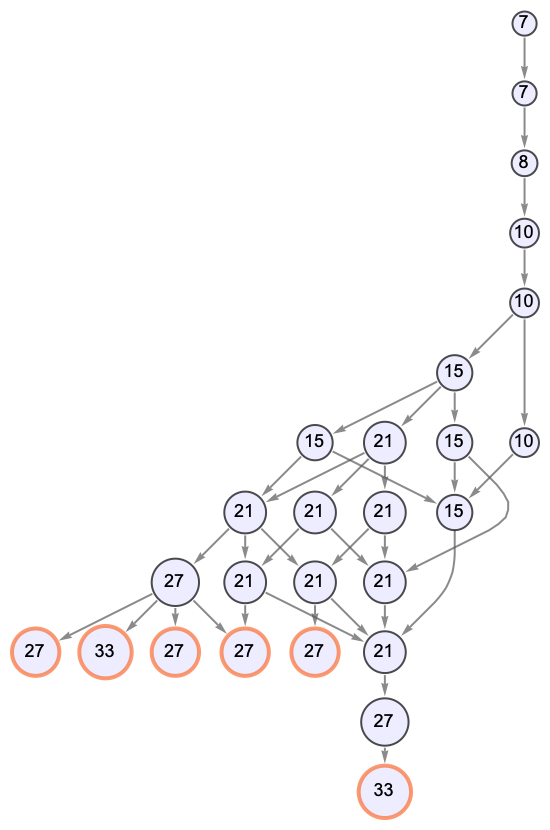 |
Show the causal structure of events in a combinator evolution according to the single-match rightmost-innermost evaluation scheme:
| In[5]:= |
| Out[5]= |  |
Highlight the state transformation path for a combinator expression evolved with a rightmost-innermost evaluation scheme, using options to omit vertex labels, make the nodes smaller and increase the thickness of edges along the path:
| In[6]:= | ![ResourceFunction["CombinatorEvolutionGraph"][
CombinatorS[CombinatorS[CombinatorS[CombinatorS]]][CombinatorS][
CombinatorS][CombinatorK], 9, "PathHighlight", "MinimalHaltedStatesGraph" -> True, "NodeSizeMultiplier" -> 0.5, "PathThickness" -> 3, "EvaluationScheme" -> {"Rightmost", "Innermost", 1}]](https://www.wolframcloud.com/obj/resourcesystem/images/dde/dde6088b-f25a-4147-be69-630d23af881a/1d27621338561157.png) |
| Out[6]= | 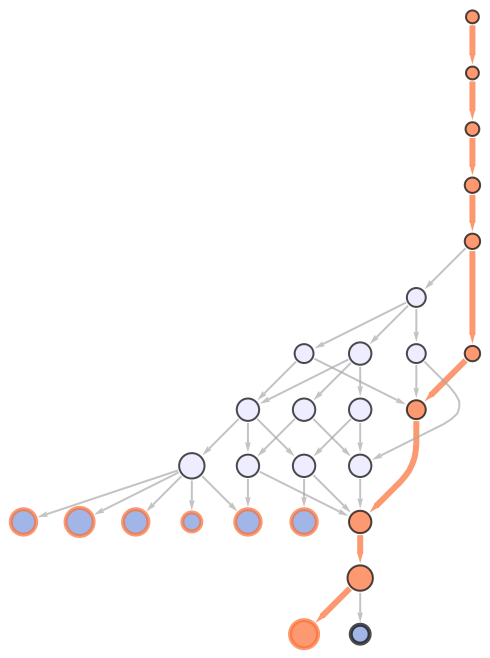 |
Show the causal structure of events in a combinator evolution according to the rightmost-innermost evaluation scheme, this time rendering vertices with the event information:
| In[7]:= | ![ResourceFunction["CombinatorEvolutionGraph"][
s[s[s[s]]][s][s][k], 9, "CausalGraph", "SKGlyphs" -> {s, k}, "EvaluationScheme" -> {"Rightmost", "Innermost", 1}, "RenderCausalEvents" -> True, AspectRatio -> 1/1.5]](https://www.wolframcloud.com/obj/resourcesystem/images/dde/dde6088b-f25a-4147-be69-630d23af881a/1bdcf85deb999b34.png) |
| Out[7]= | 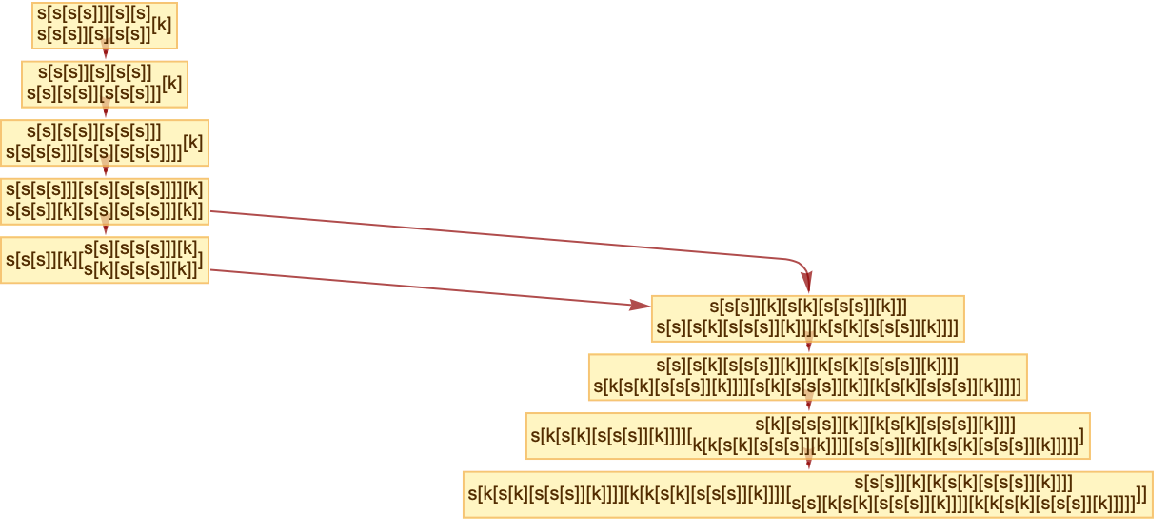 |
Specify the glyphs used for the S and K combinators in the argument cmb:
| In[8]:= |
| Out[8]= | 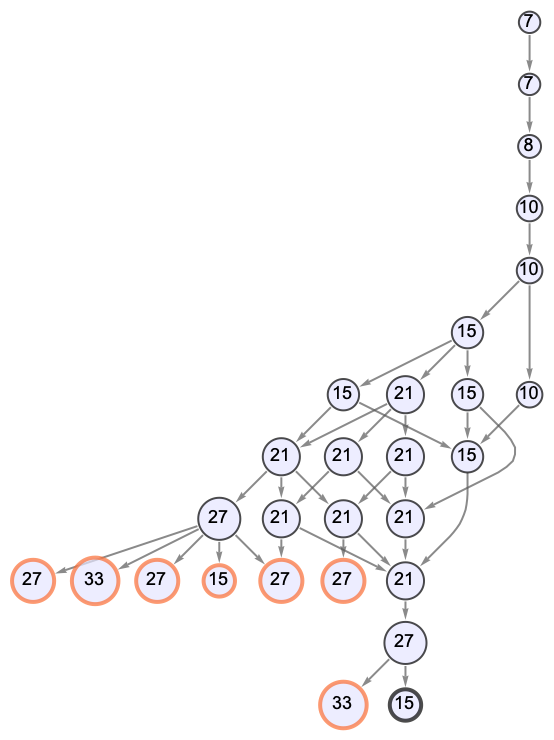 |
This work is licensed under a Creative Commons Attribution 4.0 International License