Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Collatz

Source Notebook

Get the Collatz sequence starting with a given value

Contributed by: Enrique Zeleny

ResourceFunction["Collatz"][n]

gives the Collatz sequence starting with n.

ResourceFunction["Collatz"][n,m]

gives the first m iterations.

Details

The Collatz sequence is obtained by starting from a positive integer and applying repeatedly the following operations: if the number is even, divide it by two, and if the number is odd, triple it and add one.
The Collatz conjecture states that this sequence always terminates in 1.

Examples

Basic Examples (2) 

Collatz sequence for 13:

In[1]:=
ResourceFunction["Collatz"][13]
Out[1]=

Show just the first 30 iterates for 27:

In[2]:=
ResourceFunction["Collatz"][27, 30]
Out[2]=

Applications (4) 

Highlight odd values:

In[3]:=
If[OddQ[#], Style[#, 18], #] & /@ ResourceFunction["Collatz"][27]
Out[3]=

Plot all the iterates for 27:

In[4]:=
ListLinePlot[ResourceFunction["Collatz"][27]]
Out[4]=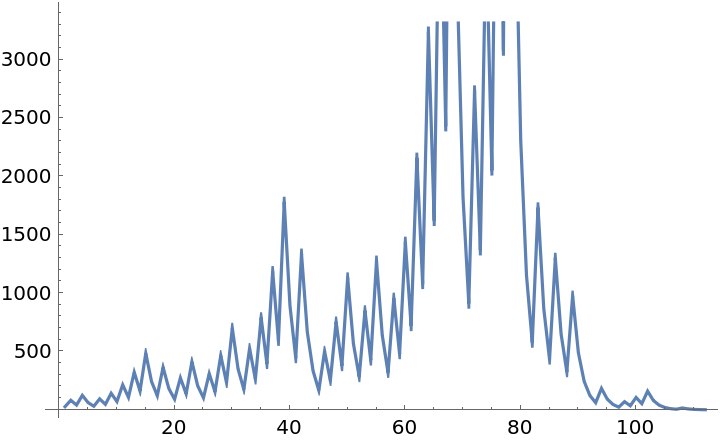

Plot the number of iterates needed for the first 100 integers:

In[5]:=
DiscretePlot[Length@ResourceFunction["Collatz"][n], {n, 100}]
Out[5]=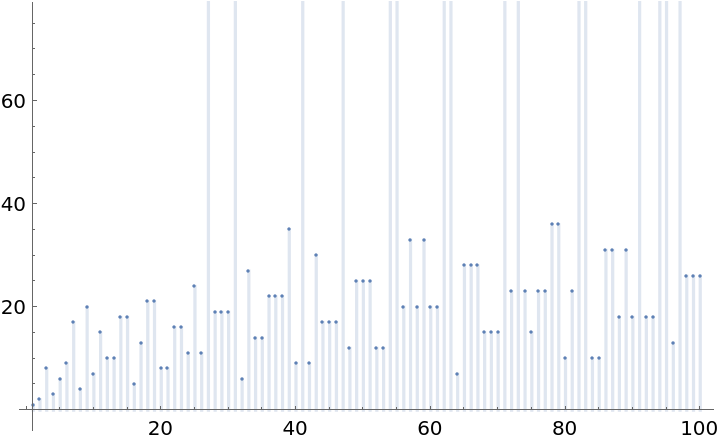

Number of iterates needed for the first 2000 integers:

In[6]:=
ListPlot[Table[{n, Length@ResourceFunction["Collatz"][n]}, {n, 2000}]]
Out[6]=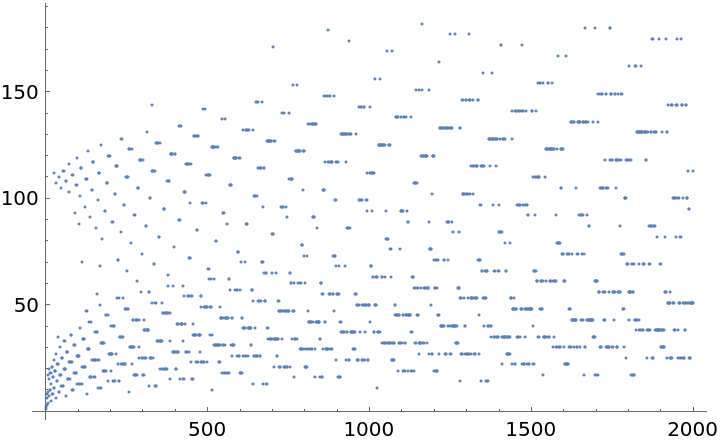

Paths of the iterates for the first 100 integers:

In[7]:=
ListPlot[Table[{n, #} & /@ ResourceFunction["Collatz"][n], {n, 100}], PlotRange -> {{0, 100}, {0, 200}}]
Out[7]=

Neat Examples (2) 

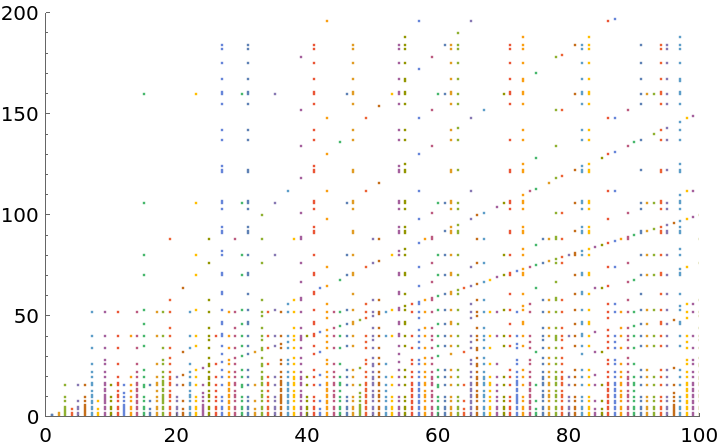Graph of the iterates for the first 26 integers:

In[8]:=
GraphPlot[ Union[Flatten[ Table[Apply[Rule, Partition[ResourceFunction["Collatz"][n], 2, 1], {1}], {n, 3, 26}]]], GraphLayout -> "SpringElectricalEmbedding", VertexLabels -> Placed["Name", Center], VertexSize -> 0.75]
Out[8]=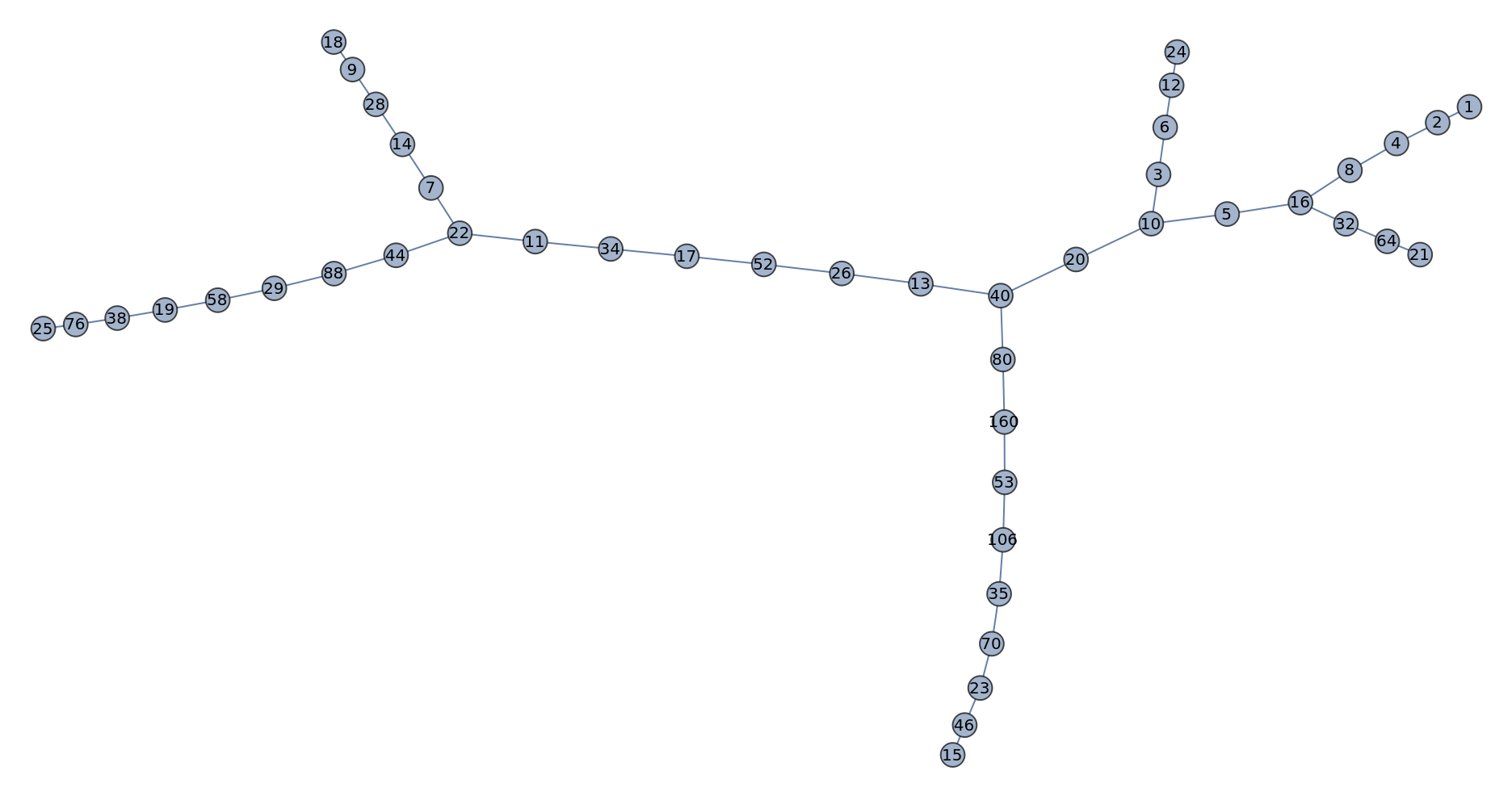

Graph of the iterates for 500:

In[9]:=
Graph[Union[ Flatten[Table[ Rule @@@ Partition[ResourceFunction["Collatz"][n], 2, 1], {n, 3, 500}]]]]
Out[9]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 13 September 2021
  • 1.0.0 – 12 February 2019

License Information