Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ClenshawCurtisQuadratureWeights

Source Notebook

Get a numerically sorted list of abscissa-weight pairs for Clenshaw-Curtis quadrature

Contributed by: Jan Mangaldan

ResourceFunction["ClenshawCurtisQuadratureWeights"][n,{a,b}]

gives a list of the n pairs {xi,wi} of the n-point Clenshaw-Curtis formula for quadrature on the interval a to b, where wi is the weight of the abscissa xi.

ResourceFunction["ClenshawCurtisQuadratureWeights"][n,{a,b},prec]

uses the working precision prec.

Details and Options

Clenshaw-Curtis approximates the value of an integral as a linear combination of values of the integrand evaluated at abscissas xi: .
Clenshaw-Curtis quadrature uses extrema of the Chebyshev polynomial ChebyshevT, augmented with ±1 and rescaled to the interval (a,b), as the abscissa values.
The precision argument acts similarly to the WorkingPrecision option used in many Wolfram Language numeric functions; it is not at all like the PrecisionGoal option. If the n argument is too small to allow for a high-precision result, extra precision in a result will not be meaningful.

Examples

Basic Examples (2) 

The abscissas and weights for a 10-point Clenshaw-Curtis quadrature on a given interval:

In[1]:=
ResourceFunction["ClenshawCurtisQuadratureWeights"][10, {-2., 9.}]
Out[1]=

Use the specified precision:

In[2]:=
ResourceFunction["ClenshawCurtisQuadratureWeights"][3, {-1, 1}, 20]
Out[2]=

Applications (4) 

Use Clenshaw-Curtis quadrature to approximate the area under a curve:

In[3]:=
f = x |-> Cos[x] + 3 x^3 - x + 3
Out[3]=

Plot the curve over a given interval:

In[4]:=
Plot[f[x], {x, -0.5, 1.5}, Filling -> Axis, AxesOrigin -> {0, 0}]
Out[4]=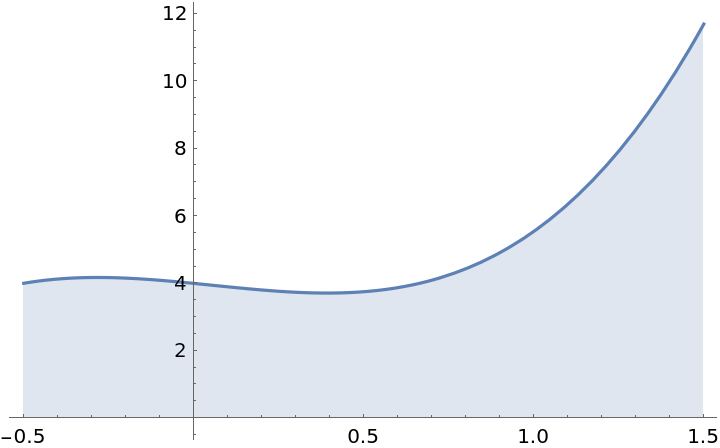

Approximate the area under the curve using n-point Clenshaw-Curtis quadrature:

In[5]:=
area[n_] := Module[{a, w}, {a, w} = Transpose@ ResourceFunction["ClenshawCurtisQuadratureWeights"][ n, {-0.5, 1.5}]; w . (f /@ a)]
In[6]:=
area[5]
Out[6]=

Compare to the output of NIntegrate:

In[7]:=
NIntegrate[f[x], {x, -0.5, 1.5}]
Out[7]=
In[8]:=
Abs[% - area[9]]
Out[8]=

Properties and Relations (1) 

The abscissas of n-point Clenshaw-Curtis quadrature are the extrema of the Chebyshev polynomial Tn-1(x), along with the interval extrema ±1:

In[9]:=
ResourceFunction["ClenshawCurtisQuadratureWeights"][ 6, {-1, 1}][[All, 1]]
Out[9]=
In[10]:=
Join[{-1.}, x /. NSolve[D[ChebyshevT[5, x], x], x], {1.}]
Out[10]=

Version History

  • 1.0.0 – 04 January 2021

Source Metadata

  • Citation:
    • Sommariva, A., "Fast construction of Fejér and Clenshaw–Curtis rules for general weight functions." Computers & Mathematics with Applications, vol. 65, no. 4, 682-693, 2013. DOI: 10.1016/j.camwa.2012.12.004
    • Trefethen, L.N., "Is Gauss Quadrature Better than Clenshaw–Curtis?" SIAM Review, vol. 50, no. 1, 67–87, 2008. DOI: 10.1137/060659831
    • Waldvogel, J., "Fast construction of the Fejér and Clenshaw–Curtis quadrature rules." BIT Numerical Mathematics, vol. 46, 195–202, 2006. DOI: 10.1007/s10543-006-0045-4

Related Resources

License Information