Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CircularStandardDeviation

Source Notebook

Compute the circular standard deviation

Contributed by: Sander Huisman

ResourceFunction["CircularStandardDeviation"][list]

calculates the circular standard deviation for the circular data list.

ResourceFunction["CircularStandardDeviation"][list→weights]

calculates the circular standard deviation for the circular data list using the weights weights.

Details

The data is assumed to be in radians.
This function calculate the standard deviation of data assuming it is in a periodic domain of 0 to 2π. The input data can have any value and does not need to be in this range. This standard deviation takes into account the discontinuity around 0 and2π for calculating the standard deviation.

Examples

Basic Examples (1) 

Calculate the circular standard deviation from some data:

In[1]:=
data = {0.3, 0.1, 0.05, 6.2, 6.1}; ResourceFunction["CircularStandardDeviation"][data]
Out[2]=

Scope (1) 

Provide weights:

In[3]:=
data = {0.3, 0.1, 0.05, 6.2, 6.1}; weights = {0.1, 1, 1, 1, 0.1}; ResourceFunction["CircularStandardDeviation"][data -> weights]
Out[5]=

Properties and Relations (2) 

Visualize some data:

In[6]:=
data = {0.3, 0.1, 0.05, 6.2, 6.1}; Graphics[{Circle[], PointSize[Large], Point[AngleVector /@ data]}]
Out[7]=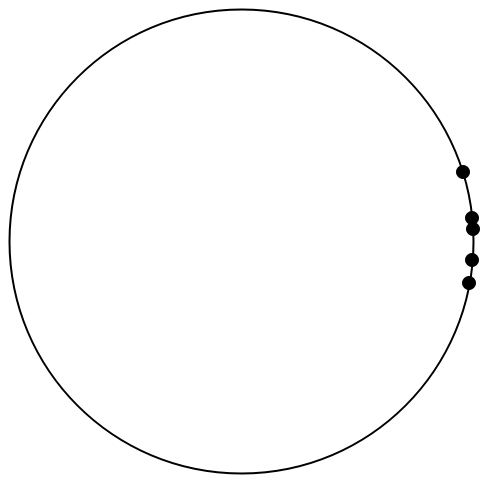

Using the standard StandardDeviation does not take into account the circularity and the result will be much larger:

In[8]:=
StandardDeviation[data]
Out[8]=

Taking the circular nature into account give the expected result:

In[9]:=
ResourceFunction["CircularStandardDeviation"][data]
Out[9]=

The definition of the function agrees such that a narrow distribution gives the expected result:

In[10]:=
data = RandomVariate[NormalDistribution[2.5, 0.2], 1000]; ResourceFunction["CircularStandardDeviation"][data]
Out[11]=

Possible Issues (2) 

An empty list spawns an error but returns 0:

In[12]:=
ResourceFunction["CircularStandardDeviation"][{}]
Out[12]=

The data and the weights should be commensurate:

In[13]:=
ResourceFunction[ "CircularStandardDeviation"][{1, 1.2, 1.1} -> {1, 1, 3, 4}]

Neat Examples (1) 

The circular standard deviation of a circular uniform distribution is ∞ but numerically it converges extremely slowly to this value:

In[14]:=
Table[{p, ResourceFunction["CircularStandardDeviation"][ RandomReal[{0, 2 Pi}, 10^p]]}, {p, 8}] // Grid
Out[14]=

Publisher

SHuisman

Version History

  • 1.0.0 – 12 November 2025

Related Resources

License Information