Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the trigonometric circular moment
ResourceFunction["CircularMoment"][list,p] calculates the p-th power trigonometric circular moment of list. | |
ResourceFunction["CircularMoment"][list→weights,p] uses the weights weights. |
Calculate the magnitude and angle of the second moment of some angular data:
| In[1]:= |
| Out[1]= |
Use some weights:
| In[2]:= | ![data = {0.3, 0.1, 0.05, 6.2, 6.1};
weights = {0.1, 1, 1, 1, 0.1};
ResourceFunction[
"CircularMoment", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][data -> weights, 2]](https://www.wolframcloud.com/obj/resourcesystem/images/8d3/8d3d0e47-9fd4-4933-a2df-bf44714b6a36/5ba9f51d9bd4c55a.png) |
| Out[4]= |
Powers do not have to be integers:
| In[5]:= |
| Out[5]= |
The first order agrees with the "CircularMean" resource function:
| In[6]:= |
| Out[7]= |
An empty list spawns an error:
| In[8]:= |
| Out[8]= |
The data and the weights should have the same lengths:
| In[9]:= |
| Out[9]= |
Visualize the circular moment for the first 10 powers of some random data that is uniformly distributed between 0 and π/3:
| In[10]:= | ![SeedRandom[1];
data = RandomReal[{0, Pi/3}, 100];
data = Table[
cm = ResourceFunction[
"CircularMoment", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][data, p];
{p, AngleVector[{cm["Magnitude"], cm["Angle"]}]}, {p, 10}];
Graphics[{Red, Arrow[{{0, 0}, #2}], Text[#1, #2 + 0.1 Normalize[#2]]} & @@@ data, Axes -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/8d3/8d3d0e47-9fd4-4933-a2df-bf44714b6a36/5d4d0b4c06888e83.png) |
| Out[13]= | 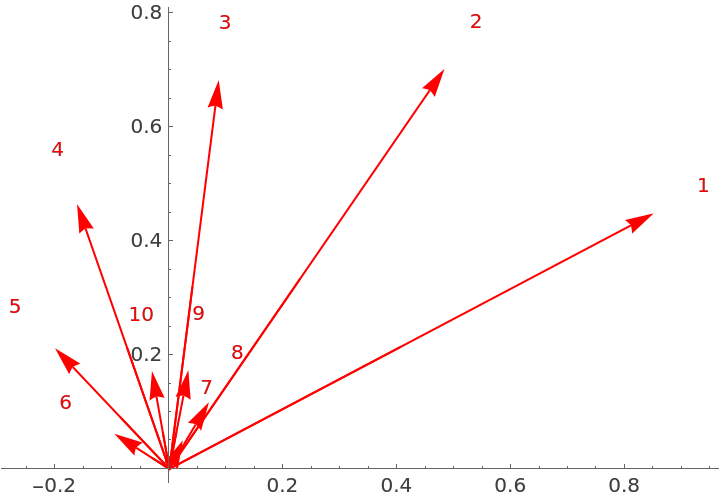 |
Plot the magnitude as a function of the power:
| In[14]:= | ![data = {0.3, 0.1, 0.05, 6.2, 6.1};
cm = ResourceFunction[
"CircularMoment", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][data, a];
Plot[cm["Magnitude"], {a, 0, 30}]](https://www.wolframcloud.com/obj/resourcesystem/images/8d3/8d3d0e47-9fd4-4933-a2df-bf44714b6a36/2b19d807e4a747b5.png) |
| Out[16]= | 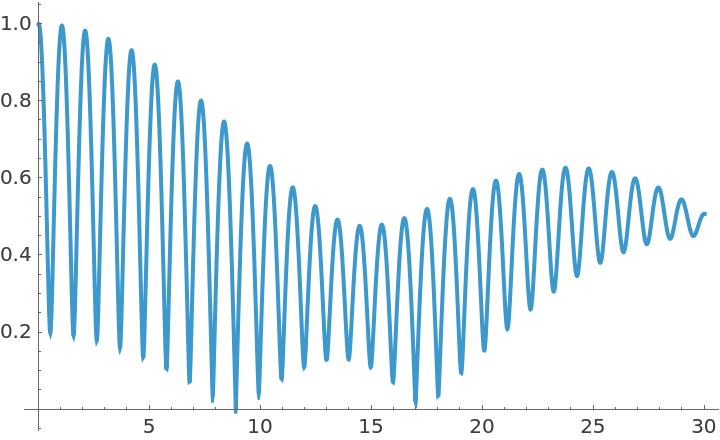 |
This work is licensed under a Creative Commons Attribution 4.0 International License