Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 CirculantMatrix

Source Notebook

Construct a circulant matrix from a vector

Contributed by: Arnoud Buzing

ResourceFunction["CirculantMatrix"][{c1,c2,…,cn}]

gives the circulant matrix whose first column consists of entries c1,c2, ….

Details and Options

A circulant matrix is a square Toeplitz matrix in which all of the columns are cyclic permutations of the first column.

Examples

Basic Examples (1) 

Compute a circulant matrix:

In[1]:=
ResourceFunction["CirculantMatrix"][{1, 2, 3, 4, 5, 6}] // MatrixForm
Out[1]=

Properties & Relations (2) 

Multiplying a circulant matrix with a vector can be expressed as a cyclic convolution:

In[2]:=
ResourceFunction["CirculantMatrix"][Array[C, 4]] . Array[\[FormalX], 4] == ListConvolve[Array[C, 4], Array[\[FormalX], 4], 1]
Out[2]=

Multiplying a vector with a circulant matrix can be expressed as a cyclic correlation:

In[3]:=
Array[\[FormalX], 4] . ResourceFunction["CirculantMatrix"][Array[C, 4]] == ListCorrelate[Array[C, 4], Array[\[FormalX], 4], 1]
Out[3]=

Circulant matrices can be diagonalized by the Fourier matrix:

In[4]:=
fm = FourierMatrix[4]; ConjugateTranspose[fm] . ResourceFunction["CirculantMatrix"][Array[C, 4]] . fm // FullSimplify // MatrixForm
Out[5]=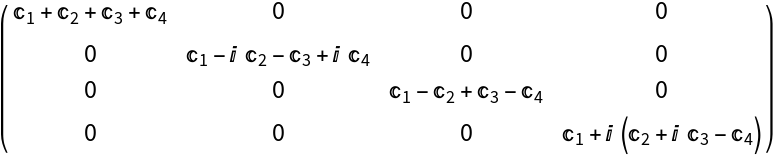

The diagonal elements of the resulting diagonal matrix are the same as the product of the Fourier matrix and the starting vector, up to a constant scaling factor:

In[6]:=
Sqrt[4] Conjugate[fm] . Array[C, 4] // FullSimplify
Out[6]=

Publisher

Arnoud Buzing

Requirements

Wolfram Language 13.3 (June 2023) or above

Version History

  • 1.0.0 – 01 December 2023

Related Resources

License Information