Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the best-fit circle for a set of points
ResourceFunction["CircleFit"][pts] returns the best-fit circle for the points pts. | |
ResourceFunction["CircleFit"][w→pts] returns the best-fit circle for the points pts having the weights w. | |
ResourceFunction["CircleFit"][w→pts,"Association"] returns an association with the center, the radius, the Circle, a pure function etc. |
Find the circle through 4 points and visualize the result:
| In[1]:= | ![pts = {{1, 2}, {2, 1}, {3, 4}, {3.5, 1.5}};
circ = ResourceFunction["CircleFit"][pts];
Graphics[{PointSize[Large], Point[pts], Red, circ}, Frame -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/e46/e46dc718-8a12-4e1c-8ca1-d3262235a583/00602e2cdc03b823.png) |
| Out[1]= | 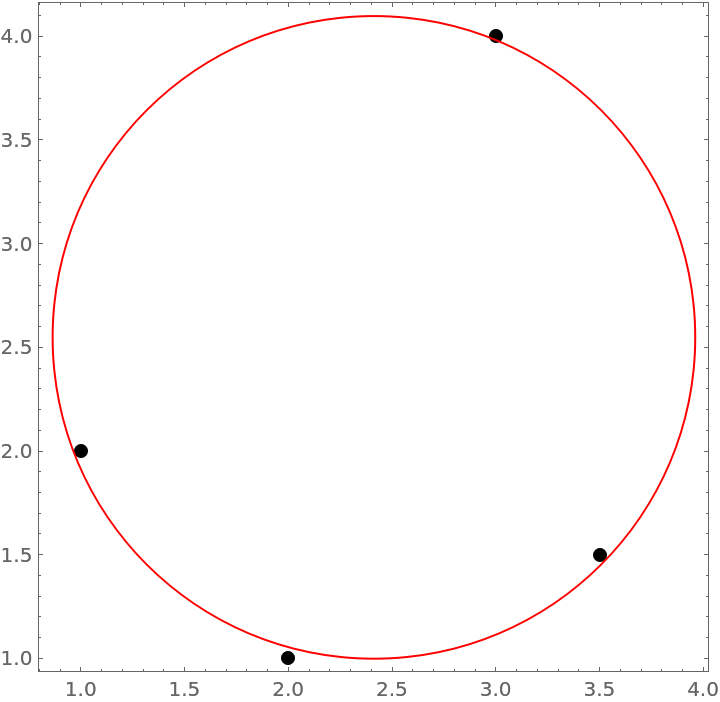 |
Find the best-fitting circle for a 2500 points:
| In[2]:= | ![SeedRandom[1234];
n = 2500;
pts = MapThread[
AngleVector[{#2, #1}] &, {RandomReal[{0, 2 Pi}, n], RandomVariate[NormalDistribution[20, 2], n]}];
circ = ResourceFunction["CircleFit"][pts];
Graphics[{Point[pts], Red, Thick, circ}, Frame -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/e46/e46dc718-8a12-4e1c-8ca1-d3262235a583/3f56fdaf18cde046.png) |
| Out[2]= | 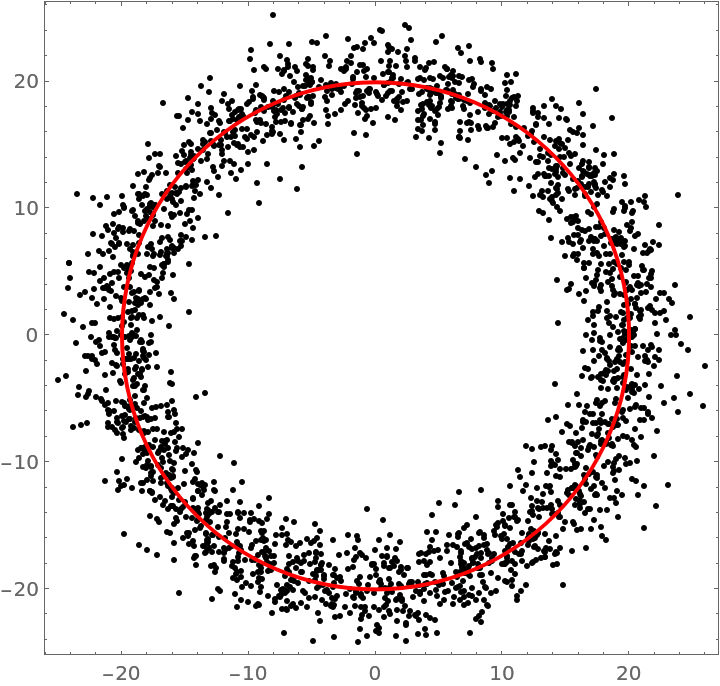 |
For 2 points, the center of the circle is the midpoints of the points:
| In[5]:= | ![pts = {{10, 5}, {8, 7}};
circ = ResourceFunction["CircleFit"][pts];
Graphics[{PointSize[Large], Point[pts], Red, circ}, Frame -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/e46/e46dc718-8a12-4e1c-8ca1-d3262235a583/129ad6bf32e67f7e.png) |
| Out[5]= | 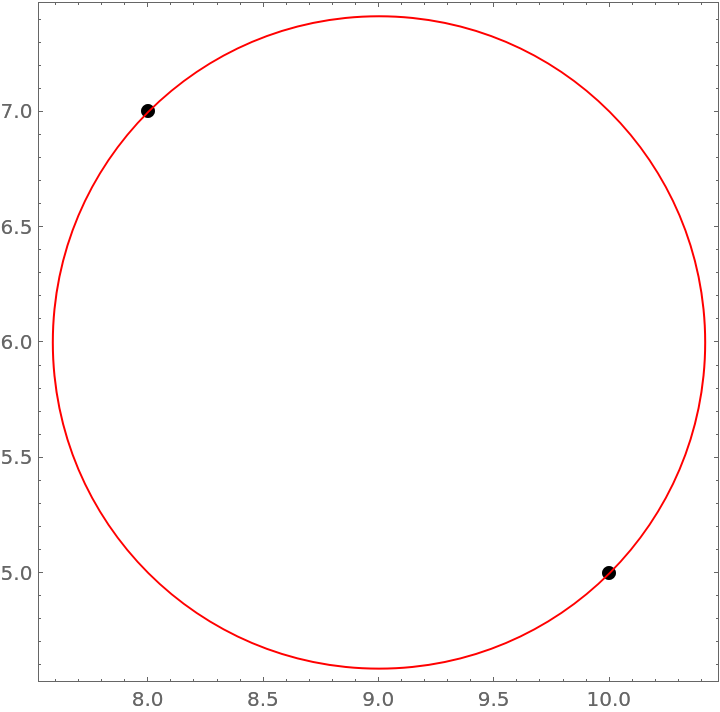 |
When no points are given, a Failure object is returned:
| In[6]:= |
| Out[6]= |
When 3 points are given and they are collinear, a Failure object is returned:
| In[7]:= |
| Out[7]= |
The case of multiple collinear points results in circle that is far away with a large radius:
| In[8]:= | ![SeedRandom[1234];
pts = Table[{0, -1} + t {2, 3}, {t, RandomVariate[NormalDistribution[], 5]}];
cc = ResourceFunction["CircleFit"][pts]](https://www.wolframcloud.com/obj/resourcesystem/images/e46/e46dc718-8a12-4e1c-8ca1-d3262235a583/2290f8f7af9f084d.png) |
| Out[8]= |
Find the best-fitting circle for points clustered around a circular arc:
| In[9]:= | ![SeedRandom[1234];
n = 1000;
pts = MapThread[
AngleVector[{10^2, 10^3}, {#2, #1}] &, {RandomReal[{0, Pi/3}, n], RandomVariate[NormalDistribution[400, 20], n]}];
circ = ResourceFunction["CircleFit"][pts];
Graphics[{Point[pts], Red, circ}, Frame -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/e46/e46dc718-8a12-4e1c-8ca1-d3262235a583/0382e8f54aff0e21.png) |
| Out[9]= | 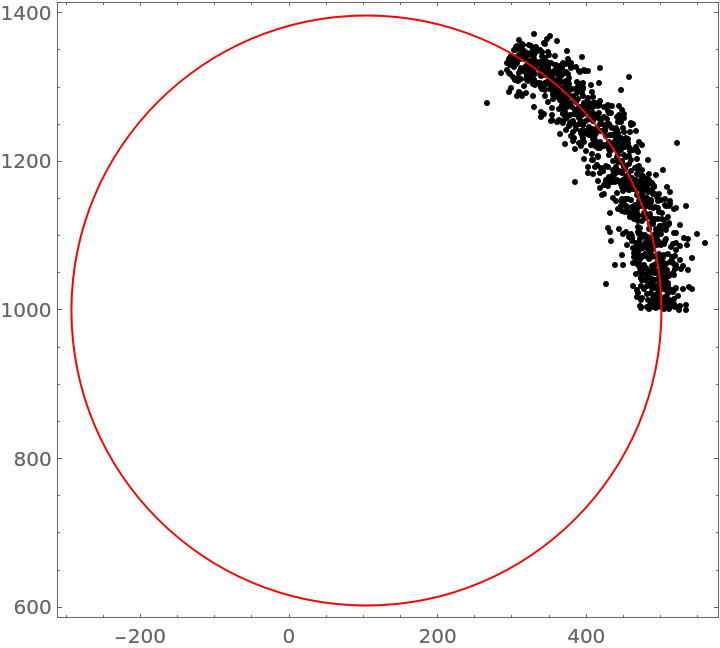 |
This work is licensed under a Creative Commons Attribution 4.0 International License